平衡树学习笔记（一）：二叉搜索树、常见的平衡树

二叉搜索树

众所周知，一个区间可以有许多信息(最大值、\(k\) 大值、区间和、区间平方和、区间立方和、区间异或和、区间 \(\gcd\)、不同数字个数、颜色段数……)，也有许多修改方式(插入、删除、区间加、区间乘、区间改、区间翻转……)，我们发现其中一些用线段树不是很好维护，这时我们可能会用到平衡树，下面来看一道例题：

P3369 【模板】普通平衡树

写一种数据结构来维护一些数，其中需要提供以下操作：

插入一个数 \(x\)。
删除一个数 \(x\)。
查询 \(x\) 的排名。
查询数据结构中排名为 \(x\) 的数。
求 \(x\) 的前驱。
求 \(x\) 的后继。

我们考虑一种类似二叉树的结构，它每个节点的左儿子值永远小于自己，右儿子值永远大于自己，现在向树中插入序列 \(4, 2, 1, 3, 6, 5, 7\)，过程如图：

插入 \(4\)

插入 \(2\)，发现它比 \(4\) 小，往左子树插入。

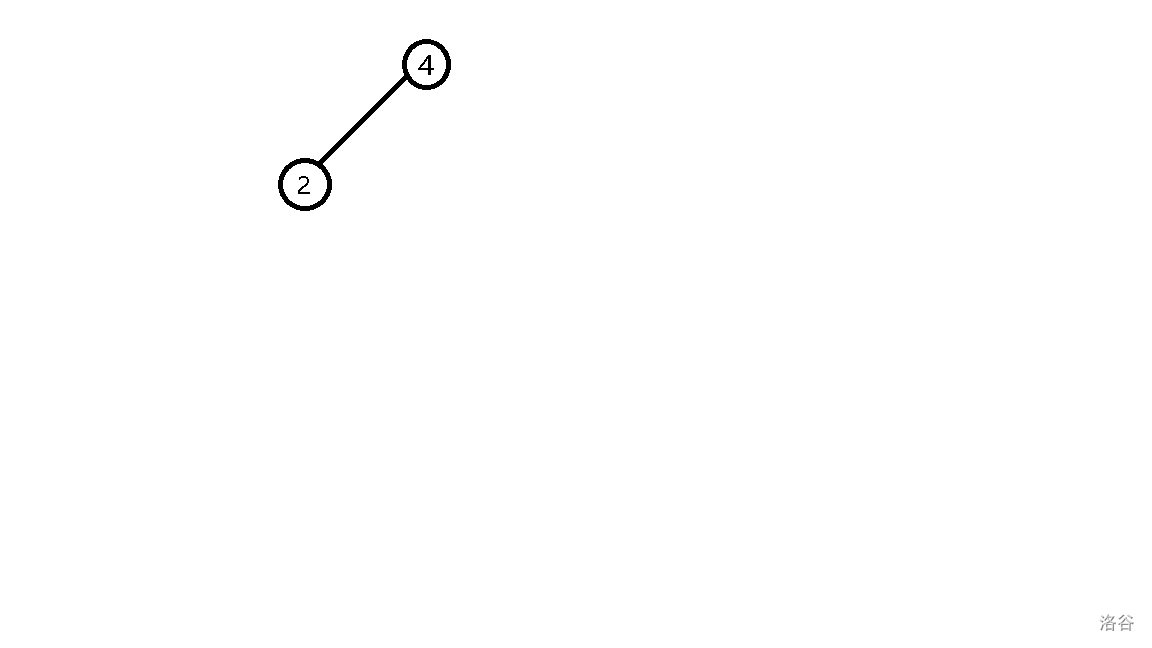
插入 \(1\)，发现它比 \(4\) 小，往左子树插入，发现它比 \(2\) 小，继续往左子树插入。

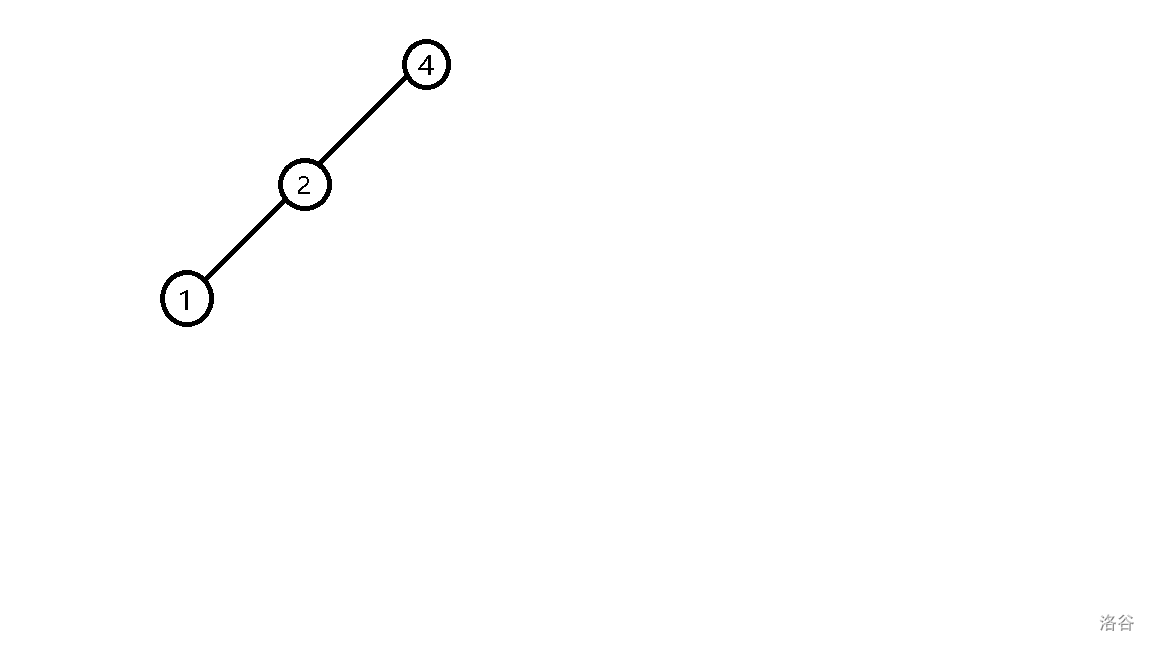
插入 \(3\)，发现它比 \(4\) 小，往左子树插入，发现它比 \(2\) 大，往右子树插入。

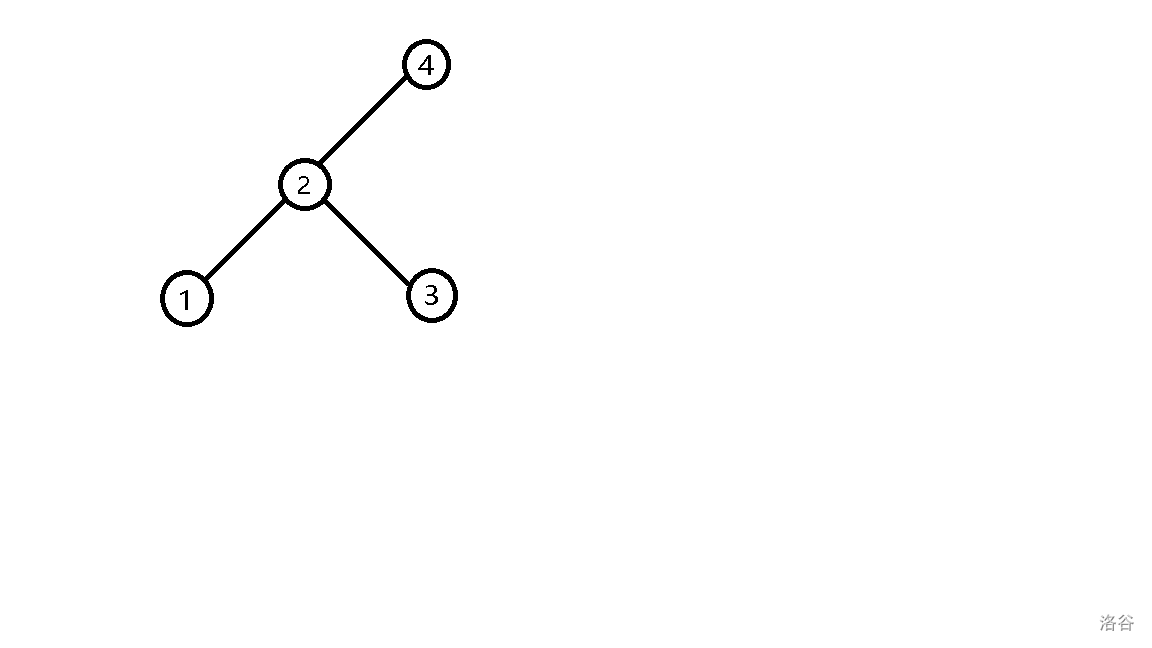
插入 \(6\)，发现它比 \(4\) 大，往右子树插入。

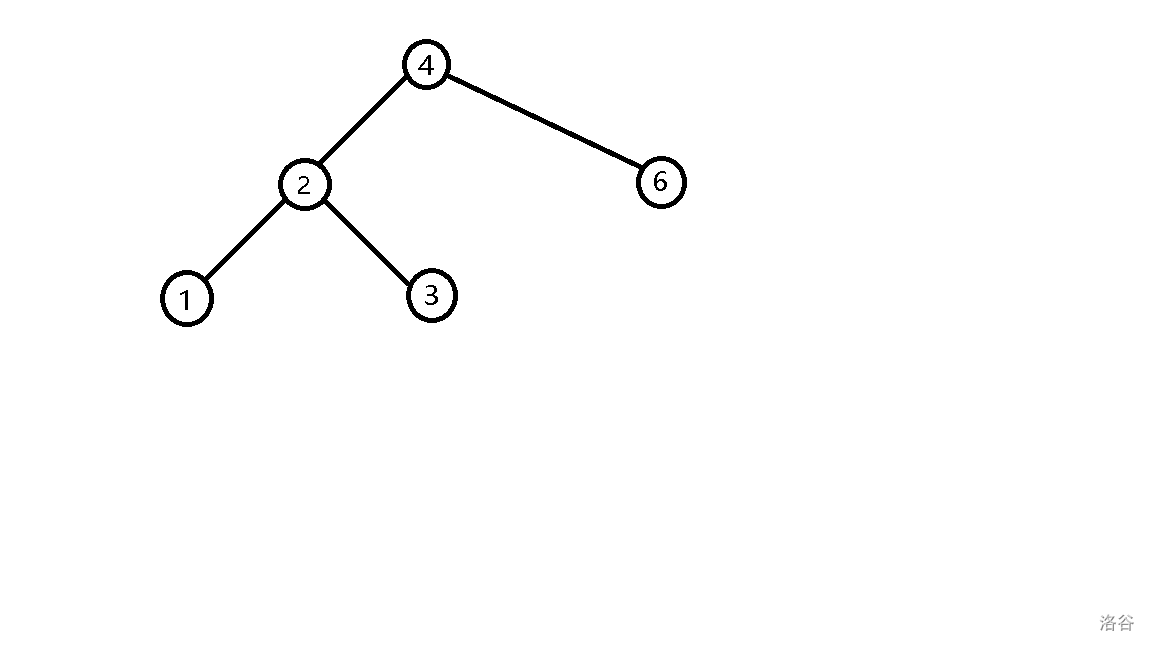
插入 \(5\)，发现它比 \(4\) 大，往右子树插入，发现它比 \(6\) 小，往左子树插入。

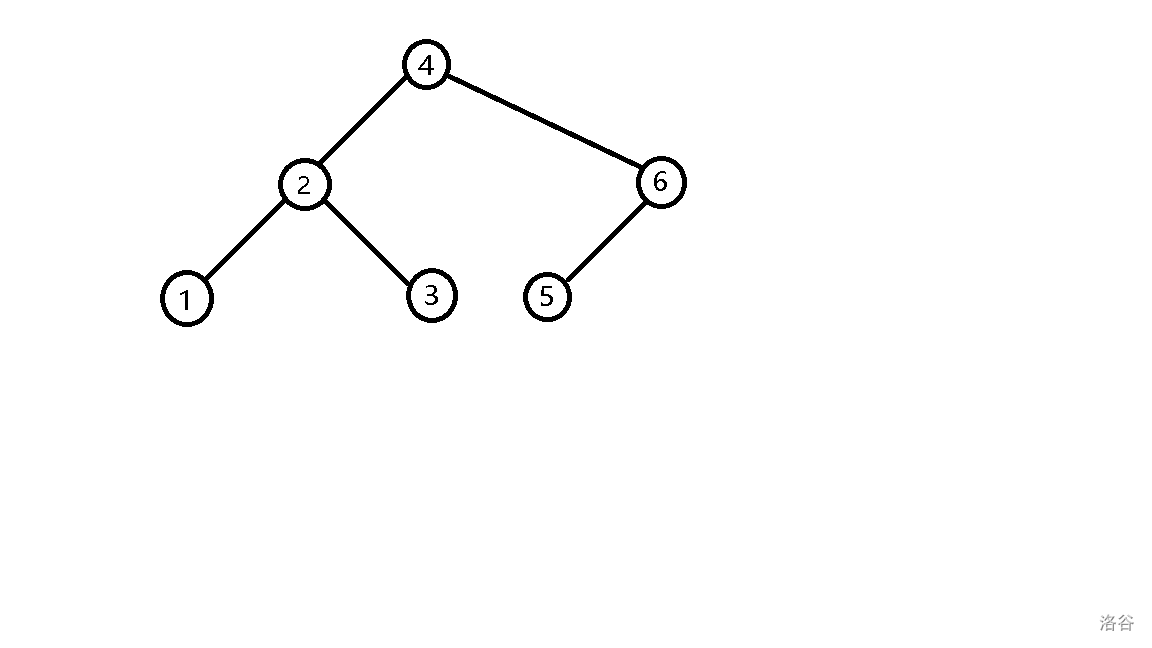
插入 \(7\)，发现它比 \(4\) 大，往右子树插入，发现它比 \(6\) 大，继续往右子树插入。

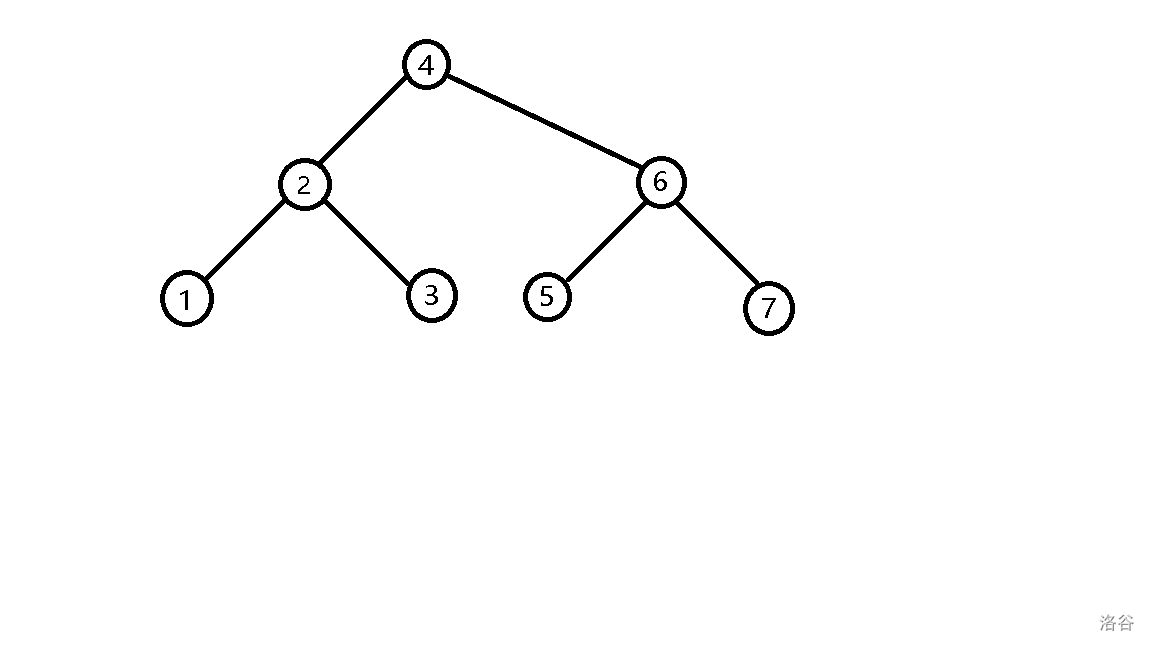
这样就建好了这棵二叉搜索树，考虑除插入外的操作如何实现。

插入代码：

void insert(int id, int val){
	if(t[id].cnt == 0){//遇到一个新节点，直接添加 
		if(flag){//当前树是空树，将这个节点设为根 
			rt = id;
			flag = false;
		}
		t[id].num = val;
		t[id].cnt = 1;
		t[id].siz = 1;
		return;
	}
	if(t[id].num == val){//遇到一个之前添加过的节点 ，直接累加 
		t[id].cnt++;
	} else if(val < t[id].num && !t[id].ls){//左儿子为空，且可以添加为左儿子，添加为左儿子 
		tot++;
		t[id].ls = tot;
		t[tot].fa = id;
		insert(t[id].ls, val);
	} else if(val > t[id].num && !t[id].rs){//右儿子为空，且可以添加为右儿子，添加为右儿子 
		tot++;
		t[id].rs = tot;
		t[tot].fa = id;
		insert(t[id].rs, val);
	} else if(val < t[id].num)//添加值比当前值小，往左子树插入 
		insert(t[id].ls, val);
	else//添加值比当前值大，往右子树插入 
		insert(t[id].rs, val);
	t[id].siz = t[id].cnt + t[t[id].ls].siz + t[t[id].rs].siz;//更新以当前节点为根的子树大小 
}

删除操作

先在二叉搜索树中找到这个 \(x\)，考虑 \(x\) 出现的次数与 \(x\) 在树中的位置，分类讨论：

如果 \(x\) 的出现次数不为 \(1\)，只用减少它的出现次数。
如果 \(x\) 的出现次数为 \(1\)
- 如果 \(x\) 是叶子节点，直接删除。
- 如果 \(x\) 只有 \(1\) 个儿子，直接将 \(x\) 替换为它的儿子。
- 如果 \(x\) 有两个儿子，一般用 \(x\) 左子树的最大值或它右子树的最小值替换它。

删除代码：

int query_min(int id){//查询以id为根的子树中的最小值 
	if(!t[id].ls)//无法再往左儿子跳 
		return t[id].num;//返回当前值 
	return query_min(t[id].ls);//往左儿子跳
}
void del(int id, int val){
	if(t[id].cnt == 0)
		return;
	if(val < t[id].num){//删除值比当前值小，往左子树递归 
		del(t[id].ls, val);
		t[id].siz = t[id].cnt + t[t[id].ls].siz + t[t[id].rs].siz;
		return;
	}
	if(val > t[id].num){//删除值比当前值大，往右子树递归 
		del(t[id].rs, val);
		t[id].siz = t[id].cnt + t[t[id].ls].siz + t[t[id].rs].siz;
		return;
	}
	if(t[id].cnt > 1){
		t[id].cnt--;
		t[id].siz = t[id].cnt + t[t[id].ls].siz + t[t[id].rs].siz;
		return;
	}
	if(!t[id].ls && !t[id].rs){//情况1.1 
		t[id].cnt = 0;
		t[id].siz = 0;
		int fa = t[id].fa;
		if(fa == 0)
			flag = true;
		else {
			if(id == t[fa].ls)
				t[fa].ls = 0;
			else
				t[fa].rs = 0;
			t[fa].siz = t[fa].cnt + t[t[fa].ls].siz + t[t[fa].rs].siz;
		}	
		t[id].num = INF;
		t[id].fa = 0;
	} else if(t[id].ls && !t[id].rs){//情况2.1 
		t[id].cnt = 0;
		t[id].siz = 0;
		int fa = t[id].fa;
		if(fa != 0){
			if(id == t[fa].ls)
				t[fa].ls = t[id].ls;
			else
				t[fa].rs = t[id].ls;
			t[fa].siz = t[fa].cnt + t[t[fa].ls].siz + t[t[fa].rs].siz;
		} else
			rt = t[id].ls;
		t[t[id].ls].fa = fa;
		t[id].num = INF;
		t[id].ls = 0;
		t[id].fa = 0;
	} else if(!t[id].ls && t[id].rs){//情况2.2 
		t[id].cnt = 0;
		t[id].siz = 0;
		int fa = t[id].fa;
		if(fa != 0){
			if(id == t[fa].ls)
				t[fa].ls = t[id].rs;
			else
				t[fa].rs = t[id].rs;
			t[fa].siz = t[fa].cnt + t[t[fa].ls].siz + t[t[fa].rs].siz;
		} else
			rt = t[id].rs;
		t[t[id].rs].fa = fa;
		t[id].num = INF;
		t[id].rs = 0;
		t[id].fa = 0;
	} else {//情况2.3 
		int tmp = query_min(t[id].rs);
		t[id].num = tmp;
		del(t[id].rs, tmp);
		t[id].siz = t[id].cnt + t[t[id].ls].siz + t[t[id].rs].siz;
	}
}

查询 \(x\) 的排名

每次将 \(x\) 与当前根比较，如果 \(x\) 比当前根小就往左子树递归，如果 \(x\) 比当前根大，就将答案累加上左子树大小与当前根的出现次数，往右子树递归，最后答案加上终点的左儿子子树大小加一。

查询 \(x\) 的排名代码：


int rk(int id, int val){
	if(id == 0)
		return 0;
	if(t[id].num == val)
		return t[t[id].ls].siz + 1;//左子树大小加1就是排名 
	else if(t[id].num > val)
		return rk(t[id].ls, val);
	else
		return rk(t[id].rs, val) + t[t[id].ls].siz + t[id].cnt;
}

查询排名为 \(x\) 的数

每次将 \(x\) 与当前根比较。

如果当前根左子树大小大于等于 \(x\)，则该元素在左子树中
如果当前根左子树大小在区间 \([x - 1, x - t[id].sum]\) 之间，则该元素为当前根节点
其它情况则在右子树中。

查询排名为 \(x\) 的数代码：

int kth(int id, int k){
	if(t[id].ls){
		if(t[t[id].ls].siz >= k)//情况1 
			return kth(t[id].ls, k);
		if(t[t[id].ls].siz + t[id].cnt >= k)//情况2
			return t[id].num;
	} else {//特判，如果当前数字添加次数比询问值大，直接返回当前值 
		if(k <= t[id].cnt)
			return t[id].num;
	}
	return kth(t[id].rs, k - t[t[id].ls].siz - t[id].cnt);//情况3 
}

查询 \(x\) 的前驱

先求出 \(x\) 在区间中的排名，因为这个排名表示比 \(x\) 小的数的个数，因此查这个排名对应的元素就是他的前驱。

查询 \(x\) 的后继

首先，\(x\) 可能有多个，因此我们要先查 \(x + 1\) 的排名，这就是小于等于 \(x\) 的数的个数，将这个数加 \(1\) 再查排名为这个数的数，就是他的后继。

完整代码：LOJ #104. 普通平衡树

~~LOJ上居然过了，而且跑的飞快~~

当你把它交到洛谷上，发现居然T了一个点，考虑有序将数添加入平衡树，你会发现这棵树退化成了一条链：

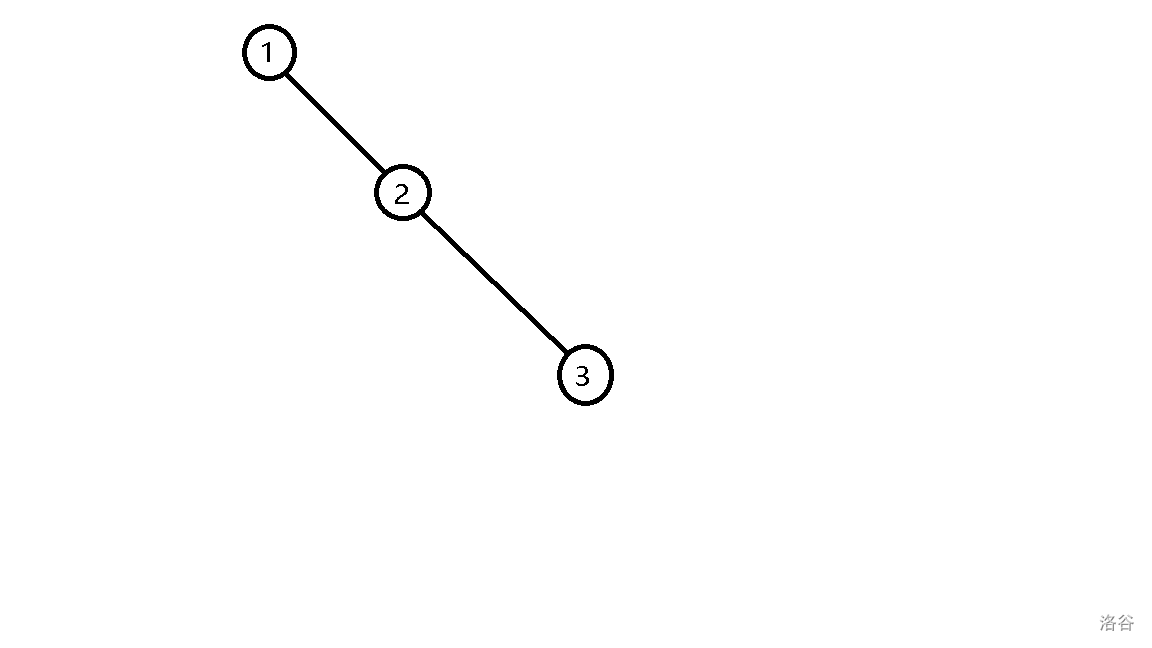
查询复杂度从 \(O(\log n)\) 变成了 \(O(n)\)，这也是它超时的原因，平衡树的作用就是让这个树的不退化成链。

AVL

替罪羊树

Treap

完整代码：

FHQ Treap

完整代码：

#include <bits/stdc++.h>
using namespace std;
const int M = 1e6 + 9;
int cnt = 0, root = 0;
struct Node{
	int ls, rs;
	int key, pri;
	int size;
} t[M];
void newNode(int x){
	cnt++;
	t[cnt].size = 1;
	t[cnt].ls = t[cnt].rs = 0;
	t[cnt].key = x;
	t[cnt].pri = rand();
}
void Update(int u){
	t[u].size = t[t[u].ls].size + t[t[u].rs].size + 1;
}
void Split(int u, int x, int &L, int &R){
	if(u == 0){
		L = R = 0;
		return;
	}
	if(t[u].key <= x){
		L = u;
		Split(t[u].rs, x, t[u].rs, R);
	} else {
		R = u;
		Split(t[u].ls, x, L, t[u].ls);
	}
	Update(u);
}
int Merge(int L, int R){
	if(L == 0 || R == 0)
		return L + R;
	if(t[L].pri > t[R].pri){
		t[L].rs = Merge(t[L].rs, R);
		Update(L);
		return L;
	} else {
		t[R].ls = Merge(L, t[R].ls);
		Update(R);
		return R;
	}
}
int Insert(int x){
	int L, R;
	Split(root, x, L, R);
	newNode(x);
	int aa = Merge(L, cnt);
	root = Merge(aa, R);
}
void Del(int x){
	int L, R, p;
	Split(root, x, L, R);
	Split(L, x - 1, L, p);
	p = Merge(t[p].ls, t[p].rs);
	root = Merge(Merge(L, p), R);
}
void Rank(int x){
	int L, R;
	Split(root, x - 1, L, R);
	printf("%d\n", t[L].size + 1);
	root = Merge(L, R);
}
int kth(int u, int k){
	if(k == t[t[u].ls].size + 1)
		return u;
	if(k <= t[t[u].ls].size)
		return kth(t[u].ls, k);
	if(k > t[t[u].ls].size)
		return kth(t[u].rs, k - t[t[u].ls].size - 1);
}
void Precursor(int x){
	int L, R;
	Split(root, x - 1, L, R);
	printf("%d\n", t[kth(L, t[L].size)].key);
	root = Merge(L, R);
}
void Successor(int x){
	int L, R;
	Split(root, x, L, R);
	printf("%d\n", t[kth(R, 1)].key);
	root = Merge(L, R);
}
int main(){
	srand(time(NULL));
	int n;
	scanf("%d", &n);
	while(n--){
		int opt, x;
		scanf("%d%d", &opt, &x);
		switch(opt){
			case 1: Insert(x); break;
			case 2: Del(x); break;
			case 3: Rank(x); break;
			case 4: printf("%d\n", t[kth(root, x)].key); break;
			case 5: Precursor(x); break;
			case 6: Successor(x); break;
		}
	}
	return 0;
}

splay

posted @ 2024-09-20 16:54 Orange_new 阅读(97) 评论(0) 收藏举报

刷新页面返回顶部

JPGOJCZX