组合数学学习笔记（一）：组合数基础知识

一、组合数

1.递推式

\(\displaystyle\binom nm = \binom{n - 1}{m - 1} + \binom{n - 1}{m}\)

证：左边相当于从 \(n\) 个数中选 \(m\) 个数，右边枚举第 \(n\) 个数选不选。如果选，就从剩下 \(n - 1\) 个数中选 \(m - 1\) 个；如果不选，就从剩下 \(n - 1\) 个数中选 \(m\) 个。

2.对称性

\(\displaystyle\binom nm = \binom{n}{n - m}\)

证：左边相当于从 \(n\) 个数中选 \(m\) 个数留下，右边相当于从 \(n\) 个数中选 \(n - m\) 个数丢弃。

3.吸收 / 相伴等式

\(\displaystyle\frac{\displaystyle\binom nm}{\displaystyle\binom{n - 1}{m - 1}} = \frac nm\)

证：原式 \(= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{(n - 1)!}{(n - 1 - m + 1)!(m - 1)!}} = \frac{\displaystyle\frac{n!}{m!}}{\displaystyle\frac{(n - 1)!}{(m - 1)!}} = \frac nm\)

\(\displaystyle\frac{\displaystyle\binom nm}{\displaystyle\binom{n - 1}{m}} = \frac{n}{n - m}\)

证：原式 \(= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{(n - 1)!}{(n - 1 - m)!m!}} = \frac{\displaystyle\frac{n!}{(n - m)!}}{\displaystyle\frac{(n - 1)!}{(n - m - 1)!}} = \frac{n}{n - m}\)

\(\displaystyle\frac{\displaystyle\binom nm}{\displaystyle\binom{n}{m - 1}} = \frac{n - m + 1}{m}\)

证：原式 \(= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{n!}{(n - m + 1)!(m - 1)!}} = \frac{(n - m + 1)!(m - 1)!}{(n - m)!m!} = \frac{n - m + 1}{m}\)

4.上指标反转

\(\displaystyle\binom nm = (-1)^m\displaystyle\binom{m - n - 1}{m}\)

证：原式 \(= \displaystyle\frac{n^{\displaystyle\underline m}}{m!} = (-1)^m \frac{(-n)^{\displaystyle\overline m}}{m!} = (-1)^m \frac{(m - n - 1)^{\displaystyle\underline m}}{m!} = (-1)^m \binom{m - n - 1}{m}\)

5.三项式系数恒等式

\(\displaystyle\binom nm \binom mk = \binom nk \binom{n - k}{m - k}\)

证：左边相当于从 \(n\) 个数中选 \(m\) 个数，再从这 \(m\) 个数中选 \(k\) 个数，右边相当于从 \(n\) 个数中选 \(k\) 个数，这些数一定包含在要选的 \(m\) 个数中，因此就只用在剩下 \(n - k\) 个数中选 \(m - k\) 个数。

6.上指标求和

\(\displaystyle\sum_{i = 0}^n\binom im = \binom{n + 1}{m + 1}\)

证：①原式 \(= \displaystyle\sum_{i = m}^n \frac{i^{\displaystyle\underline m}}{m!}\)（当 \(i \leq m\) 时，无法从 \(i\) 个数中选出 \(m\) 个数，因此省去）\(= \displaystyle\frac{1}{m!} \sum_{i = m}^n i^{\displaystyle\underline m}\)（\(\displaystyle\frac{1}{m!}\) 与 \(i\) 无关，可以提出）\(= \displaystyle\frac{1}{m!} [\frac{(n + 1)^{\displaystyle\underline{m + 1}}}{m + 1} - \frac{m^{\displaystyle\underline{m + 1}}}{m + 1}]\)（离散微积分，具体证明可见微积分学习笔记）\(= \displaystyle\frac{(n + 1)^{\underline{m + 1}}}{(m + 1)!} = \binom{n + 1}{m + 1}\)。

②右边相当于从 \(n + 1\) 个数中选出 \(m + 1\) 个数，左边相当于确定了第 \(m + 1\) 个数的位置 \(i + 1\)，要从前 \(i\) 个数中再选 \(m\) 个。

练习一

化简：\(\displaystyle\sum_{i = 0}^{m} \binom{n + i}{i}\)

解：原式 \(= \displaystyle\sum_{i = 0}^m \binom{n + i}{n}\)（对称性）\(= \displaystyle\binom{n + m + 1}{n + 1}\) （上指标求和）。

7.下指标求和

\(\displaystyle\sum_{i = 0}^n \binom ni = 2^n\)

证：①左边相当于从 \(n\) 个数中选任意个数，每个数都有选或不选两种方案，因此有 \(2^n\) 种方案；

②当二项式定理中 \(x\) 和 \(y\) 都为 \(1\)，就可以得出此等式。

HDU6333 Harvest of Apples

一句话题意：给 \(q\) 组询问，每次给出 \(n, m\)，求\(\displaystyle\sum_{i = 0}^{m} \binom ni\)。

\(q, n, m \leq 10^5\)，对 \(10^9 + 7\) 取模。

解：把 \(n, m\) 看成区间，使用莫队算法：

\(n \rightarrow n + 1\)：\(\displaystyle\sum_{i = 0}^m \binom{n + 1}{i} = \sum_{i = 0}^m \binom ni + \sum_{i = 0}^m \binom{n - 1}{i} = 2 \sum_{i = 0}^m \binom ni - \binom nm\)（两排错位相加，减掉最后一位）

\(m \rightarrow m + 1\)：\(\displaystyle\sum_{i = 0}^{m + 1} \binom ni = \sum_{i = 0}^m \binom ni + \binom{n}{m + 1}\)

8.下指标卷积 | 范德蒙德卷积

\(\displaystyle\sum_{i = 0}^{k} \binom ni\binom{m}{k - i} = \binom{n + m}{k}\)

证：左边相当于从 \(n\) 个数中选 \(i\) 个数，再从 \(m\) 个数中选 \(k - i\) 个数，右边相当于从 \(n + m\) 个数中选 \(k\) 个数，两者意义相同。

练习二|下指标点积

化简\(\displaystyle\sum_{i = 0}^m \binom ni \binom mi\)

解：原式 \(=\displaystyle\sum_{i = 0}^m \binom ni \binom{m}{m - i}\)（对称性）= \(\displaystyle\binom{n + m}{m}\)（下指标卷积） 。

9.上指标卷积

\(\displaystyle\sum_{i = 0}^n \binom ia \binom{n - i}{b} = \binom{n + 1}{a + b + 1}\)

证：左边相当于在 \(n\) 个数中插入一个挡板，在挡板左边的数中选 \(a\) 个，在挡板右边的数中选 \(b\) 个，如果将挡板也看作一个数，那么就等于从 \(n + 1\) 个数中选 \(a + b + 1\) 个数，即右边的表达式。

练习三

化简：\(\displaystyle\sum_{i = m}^n(-1)^i\binom ni \binom im\)

解：原式 \(= \displaystyle\sum_{i = m}^n (-1)^i \binom nm \binom{n - m}{i - m}\)（三项式系数恒等式）\(= \displaystyle\binom nm\sum_{i = m}^n (-1)^i \binom{n - m}{i - m}\)（\(\displaystyle\binom nm\) 与 \(i\) 无关，可以提出）\(= \displaystyle\binom nm\sum_{i = m}^n (-1)^i \frac{(n - m)^{\displaystyle\underline{i - m}}}{(i - m)!}\)（组合数展开）\(=\displaystyle\binom nm\sum_{i = m}^n (-1)^m \frac{(i - n - 1)^{\displaystyle\underline{i - m}}}{(i - m)!}\)（上指标反转）\(= (-1)^m \displaystyle \binom nm \sum_{i = m}^n \binom{i - n - 1}{m - n - 1}\)（组合数的定义）\(= (-1)^m \displaystyle\binom nm \binom{0}{m - n} = \left\{ \begin{array}{lr} (-1)^m & : m = n \\ 0 & : m \neq n \end{array} \right.\)。

例题二

有标号连通图计数，\(n \leq 10^3\)

分析：记 \(f_i\) 表示大小为 \(i\) 的有标号连通图的个数，\(g_i\) 表示大小为 \(i\) 的有标号图的个数，则 \(g_i = 2^{\binom{n}{2}}\)。

考虑简单容斥，求大小为 \(i\) 的有标号不连通图的个数：假设 \(1\) 号点所在连通块大小为\(j(j < i)\)，则有 \(f_i = g_i -\displaystyle\sum_{j = 1}^{i - 1}\binom{i - 1}{j - 1}f_j\)

\(O(n^2)\) DP 即可。

洛谷 P2791 幼儿园篮球题

一句话题意：给定 \(L\)，\(T\) 次询问，每次给定 \(n, m, k\)，求：\(\displaystyle\sum_{i=0}^k\binom{m}{i}\binom{n - m}{k - i}i^L\)

\(T \leq 200, n, m, k \leq 2 \times 10^7, L \leq 2 \times 10^5\)

分析：原式 \(= \displaystyle\sum_{i=0}^k\binom{m}{i}\binom{n - m}{k - i}\sum_{j=0}^L {L \brace j} i^{\underline{j}}\) (斯特林数的计算式) \(= \displaystyle\sum_{i=0}^k\binom{m}{i}\binom{n - m}{k - i}\sum_{j=0}^L{L \brace j}\normalsize\binom{i}{j}j!\) (组合数的计算式) \(= \displaystyle\sum_{j=0}^L\sum_{i=0}^kj!{L \brace j}\normalsize\binom{m}{i}\binom{i}{j}\binom{n - m}{k - i}\) (将求和移动到最外层) \(= \displaystyle\sum_{j=0}^L\sum_{i=0}^kj!{L \brace j}\normalsize\binom{m}{j}\binom{m - j}{i - j}\binom{n - m}{k - i}\) (三项式系数恒等式) \(= \displaystyle\sum_{j=0}^Lj!{L \brace j}\normalsize\binom{m}{j}\sum_{i=0}^k\binom{m - j}{i - j}\binom{n - m}{k - i}\) (将只与 \(j\) 有关的因式外移) \(= \displaystyle\sum_{j=0}^Lj!{L \brace j}\normalsize\binom{m}{j}\binom{n - j}{k - j}\)

预处理一下斯特林数和组合数就可以 \(O(L)\) 每次询问了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e7 + 9, L = 1e6 + 9, MOD = 998244353;
int rev[L];
int qpow(int x, int y){
	int res = 1;
	while(y){
		if(y & 1)
			res = res * x % MOD;
		x = x * x % MOD;
		y >>= 1;
	}
	return res;
}
void NTT(int *f, int n, int opt);
int vis[L], prime[L], mi[L], t, l, nn, mm;
void get_mi(){
	mi[0] = 0;
	mi[1] = 1;
	int cnt = 0;
	for(int i = 2; i < L; i++){
		if(!vis[i]){
			vis[i] = i;
			prime[cnt++] = i;
			mi[i] = qpow(i, l);
		}
		for(int j = 0; j < cnt && i * prime[j] < L; j++){
			vis[i * prime[j]] = prime[j];
			mi[i * prime[j]] = mi[i] * mi[prime[j]] % MOD;
			if(i % prime[j] == 0)
				break;
		}
	}
}
int f[L << 1], g[L << 1], fac[N], inv[N];
int binom(int n, int m){
	if(n < m || m < 0)
		return 0;
	return fac[n] * inv[n - m] % MOD * inv[m] % MOD;
} 
signed main(){
	scanf("%lld%lld%lld%lld", &nn, &mm, &t, &l);
	fac[0] = 1;
	for(int i = 1; i <= max(nn, l); i++)
		fac[i] = fac[i - 1] * i % MOD;
	inv[max(nn, l)] = qpow(fac[max(nn, l)], MOD - 2);
	for(int i = max(nn, l) - 1; i >= 0; i--)
		inv[i] = inv[i + 1] * (i + 1) % MOD; 
	get_mi();
	for(int i = 0; i <= l; i++){
		f[i] = mi[i] * inv[i] % MOD;
		if(i % 2 == 0)
			g[i] = inv[i];
		else
			g[i] = MOD - inv[i];
	}
	int lim = 1;
	while(lim <= 2 * l)
		lim <<= 1;
	NTT(f, lim, 1);
	NTT(g, lim, 1);
	for(int i = 0; i <= lim; i++)
		f[i] = f[i] * g[i] % MOD;
	NTT(f, lim, -1);
	while(t--){
		int n, m, k, ans = 0;
		scanf("%lld%lld%lld", &n, &m, &k);
		for(int i = 0; i <= l; i++)
			ans = (ans + fac[i] * f[i] % MOD * binom(m, i) % MOD * binom(n - i, k - i) % MOD) % MOD;
		printf("%lld\n", ans * qpow(binom(n, k), MOD - 2) % MOD);
	}
	return 0;
}

10.Lucas 定理

\(\displaystyle\binom nm \equiv \binom{\lfloor\displaystyle\frac np\rfloor}{\lfloor\displaystyle\frac mp\rfloor}\binom{n \bmod p}{m \bmod p} \pmod p\)

证：① \(\because\displaystyle\binom pm \bmod p = [m = 0 \vee m = p]\)

\(\therefore (a + b)^p \equiv a^p + b^p \pmod p\)(二项式定理展开);

\(\displaystyle\binom nm = [x^m](1 + x)^n\) (\([x^i]\) 表示多项式中 \(x^i\) 项的系数，由二次项定理可得)

\(\therefore (1 + x)^n = (1 + x^{p\lfloor\frac np \rfloor})(1 + x)^{n \bmod p}\)

\(\because (1 + x^{p\lfloor\frac np\rfloor}) \equiv (1 + x^p)^{{\lfloor\frac np\rfloor}} \pmod p\) 只有产生 \(p\) 倍数处的贡献，而
\((1 + x)^{n \bmod p}\) 只在 \(0 \longrightarrow p - 1\) 处产生贡献，所以每个位置刚好被贡献一次。

② 对于素数\(m, r \in (0, m)\)

\(\displaystyle\binom mr = \frac{m!}{r!(m - r)!} = \frac{(m - 1)!}{(r - 1)!(m - r)!} \times \frac mr = \binom{m - 1}{r - 1} \times \frac mr \equiv 0 \pmod m\)

带入二项式定理的展开式，得：

\((1 + x)^m = \displaystyle\sum_{r = 0}^m\binom{m}{r}x^r = 1 + \sum_{r = 1}^{m - 1}\binom mr x^r + x^m \equiv 1 + x^m \pmod m\)

令 \(n = sm + a\)，有：

\((1 + x)^n = (1 + x)^{sm + a} = (1 + x)^{sm}(1 + x)^a \equiv(1 + x^m)^s(1 + x)^a \equiv (\displaystyle\sum_{i = 0}^s \binom si x^{im})(\sum_{j = 0}^a \binom aj x^j) \pmod m\)

又根据二项式定理 \((1 + x)^n = \displaystyle\sum_{r = 0}^n\binom nr x^r\)，与上式对比得：

\(\displaystyle\sum_{r = 0}^n\binom nr x^r \equiv (\sum_{i = 0}^s\binom si x^{im})(\sum_{j = 0}^a\binom ajx^j) \pmod m\)

对比两边第 \(x^r\) 次项的系数，根据 \(r = im + j, i = r / m, j = r \bmod m, a = n \bmod m, s = n / m\)，得：

\(\displaystyle\binom nr \equiv \binom is\binom ja \pmod m \equiv \binom{\lfloor\displaystyle\frac rm \rfloor}{\lfloor\displaystyle\frac nm \rfloor}\binom{r \bmod m}{n \bmod m} \pmod m\)

二、二项式定理

11.二项式定理

\((x + y)^n = \displaystyle\sum_{i = 0}^n \binom ni x^{n - i }y^i\)

证：第 \(i\) 项的系数等于从 \(n\) 个 \(x + y\) 中选出 \(i\) 相乘后最高项系数和

练习四|牛顿级数

记 \(\triangle^na\) 表示数列 \(a\) 差分 \(n\) 次后的数列，证明：\(\triangle^n a_i = \displaystyle\sum_{j = 0}^n (-1)^j \binom nj a_{i - j}\)

证：①：当差分一次时，式子成立；假设对于前 \(n\) 次差分，都有 \(\displaystyle\triangle^n a_i = \sum_{j = 0}^n (-1)^j \binom nj a_{i - j}\)，则 \(\triangle^{n + 1} a_i = \displaystyle\sum_{j = 0}^n (-1)^j \binom nj a_{i - j} - \sum_{j = 0}^n (-1)^j \binom{n}{j - 1} a_{i - 1 - j} = \sum_{j = 0}^n (-1)^j \binom nj a_{i - j} + \sum_{j = 1}^{n + 1} (-1)^j \binom{n}{j - 1}a_{i - j} = \sum_{j = 1}^{n + 1}(-1)^j [\binom nj + \binom{n}{j - 1}] a_{i - j} = \sum_{j = 1}^{n + 1} (-1)^j \binom{n + 1}{j} a_{i - j}\)。

符合数学归纳法，等式成立

②设 \(I_{a_i} = a_i, E_{a_i} = a_{i - 1}\)

则 \(\triangle^n a_i = (I - E)^n = \displaystyle\sum_{j = 0}^n \binom nj I^{n - j}(-E^j) = \sum_{j = 0}^n \binom nj (-E^j)\)（\(I\) 变换多少次都不会影响序列）\(= \displaystyle\sum_{j = 0}^n (-1)^j \binom nj E^j\)（将 \(-1\) 提出）\(= \displaystyle\sum_{j = 0}^n (-1)^j \binom nj a_{i - j}\)（\(E^j\) 相当于将 \(a_i\) 左移 \(j\) 位，到 \(a_{i-j}\)）。

三、错排

12.错排

记 \(f_n\) 表示长度为 \(n\) 的，且不存在 \(p_i = i\) 的排列的个数

则 \(f_n = (n - 1)(f_{n - 1} + f_{n - 2})\)

证：考虑数字 \(1\) 有 \(n - 1\) 种放法，假如放到了位置 \(k\)，那位置 \(k\) 处的数字有两种类型的放法：要么放在位置 \(1\)，那么剩下物品的放法就有 \(f_{n - 2}\) 种

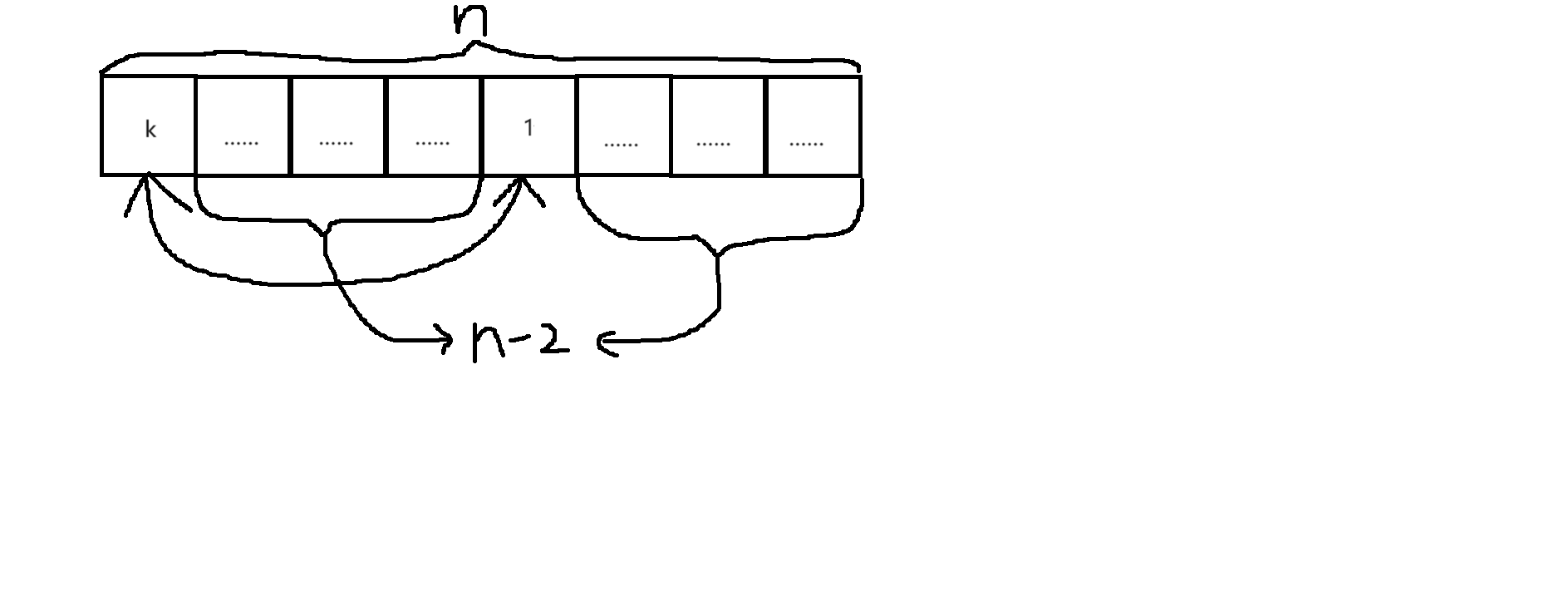
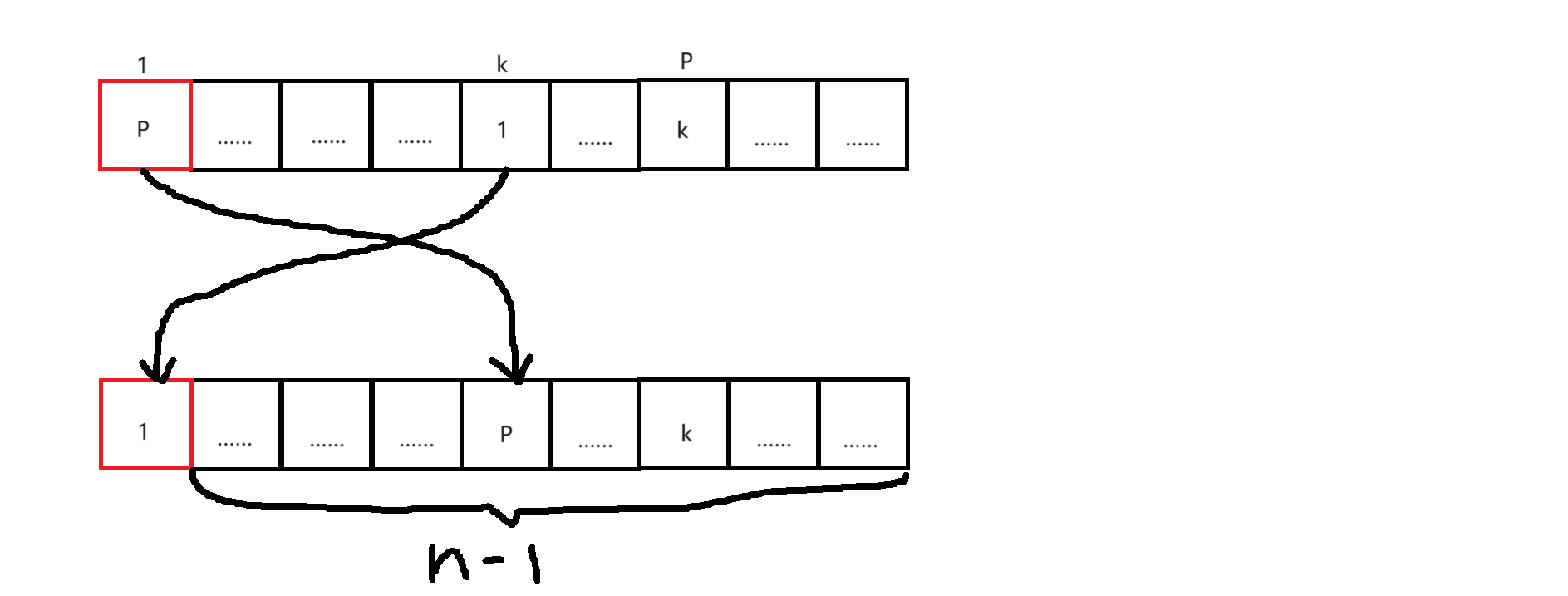
要么放在除 \(1\) 外的其他位置，那么让最后排完了时排在 \(1\) 位置的数字与排在 \(k\) 位置的数字 \(1\) 交换，不看 \(1\) 位置，就得到了一个大小为 \(n - 1\) 的错排，也就是这种情况下的每种方案可以与大小为 \(n - 1\) 的错排一一对应，故这种情况
有 \(f_{n - 1}\) 种方案。

洛谷 P7438 更简单的排列计数

一句话题意：记 \(cyc_{\pi}\) 表示将排列 \(\pi\) 看成置换，其中循环的个数。给定 \(n, k\) 和一个 \(k - 1\) 次多项式 \(F\)，对于所有 \(1 \leq n \leq m\) 求 \(\displaystyle\sum_{\pi}F(cyc_{\pi})\)

其中 \(\pi\) 表示长度为 \(m\) 的错排

\(n \leq 6 \times 10^5, k \leq 100\)，对 \(998244353\) 取模

分析：原式 \(= \displaystyle\sum_{\pi} \sum_{i = 0}^{k - 1} f_i cyc_{\pi}^i\)（将多项式展开）\(= \displaystyle\sum_{\pi} \sum_{i = 0}^{k - 1} f_i \sum_{j = 0}^i {i \brace j} \binom{cyc_{\pi}}{j} j!\)（斯特林数的计算式）\(= \displaystyle\sum_{\pi}\sum_{i = 0}^{k - 1} \sum_{j = 0}^i f_i {i \brace j} \binom{cyc_{\pi}}{j} j!\)（将求和移动到最外层）\(= \displaystyle\sum_{\pi} \sum_{j = 0}^{k - 1}\sum_{i = j}^{k - 1} f_i {i \brace j} \binom{cyc_{\pi}}{j} j!\)（交换求和顺序）\(= \displaystyle\sum_{\pi} \sum_{j = 0}^{k - 1} \binom{cyc_{\pi}}{j} j! \sum_{i = j}^{k - 1} f_i {i \brace j}\)（将只与 \(j\) 有关的因式外移）\(= \displaystyle\sum_{j = 0}^{k - 1} j! \sum_{\pi} \binom{cyc_{\pi}}{j} \sum_{i = j}^{k - 1} f_i {i \brace j}\)（将只与 \(\pi\) 有关的因式内移）

其中 \(\displaystyle\sum_{i = j}^{k - 1}f_i {i \brace j}\) 可以 \(\mathcal O(k^2)\) 预处理

记 \(C_{t, i}\) 表示有 \(i\) 个循环，长度为 \(t\) 的错排数

则 \(C_{t, i} = (t - 1)(C_{t - 2, i - 1} + C_{t - 1, i})\)（与错排递推式推导类似）

记 \(P_{t, i} = \displaystyle\sum_{|\pi| = t} \binom{cyc_{\pi}}{i}\)

考虑枚举循环个数，当循环个数为 \(j\) 时，有 \(C_{t, j}\) 种排法，每种排法对 \(P_{t, i}\) 的贡献为 \(\displaystyle\binom ji\)

则 \(P_{t, i} = \displaystyle\sum_{j = 1}^t \binom ji C_{t, j} = \sum_{j = 1}^t \binom ji [(t - 1)(C_{t - 2, j - 1} + C_{t - 1, j})] = (t - 1)\sum_{j = 1}^t \binom ji (C_{t - 2, j - 1} + C_{t - 1, j})\)（将常量外移）\(= (t - 1)\displaystyle\sum_{j = 1}^t \binom ji C_{t - 2, j - 1} + (t - 1) \sum_{j = 1}^t \binom ji C_{t - 1, j}\)（拆括号）\(= (t - 1) \displaystyle\sum_{j = 1}^t(\binom{j - 1}{i} + \binom{j - 1}{i - 1}) C_{t - 2, j - 1} + (t - 1) \sum_{j = 1}^t \binom ji C_{t - 1, j}\)（组合数递推式逆用）\(= (t - 1)\displaystyle\sum_{j = 1}^t \binom{j - 1}{i} C_{t - 2, j - 1} + \binom{j - 1}{i - 1} C_{t - 2, j - 1} + (t - 1) \sum_{j = 1}^t \binom ji C_{t - 1, j} = (t - 1)(P_{t - 2, i} + P_{t - 2, i - 1} + P_{t - 1, i})\)

于是 \(O(nk + k^2)\) 预处理一下之后，对于每个 \(m\)，\(O(k)\) 求答案即可。