数据挖掘算法与应用（python）之数据探索与预处理

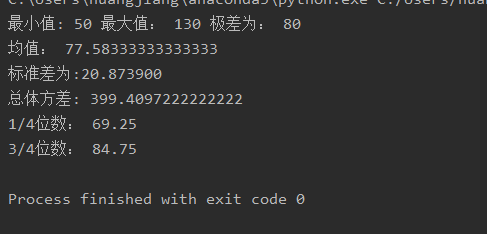
1.求中位数、平均数、众数、最大值、最小值、四分位数、标准差以及方差。(数据来源:例2.1)50,51,67,70,72,72,76,80,83,90,90,130

 

l=[50,51,67,70,72,72,76,80,83,90,90,130]

print("最小值:",min(l),"最大值：",max(l),"极差为：",max(l)-min(l))
print("均值：", (sum(l)/len(l)))    #带模块的均值的其他求法：1、statistics.mean(l)  2、np.meean(l)

#import statistics
#print("中位数：",statistics.median(l) ,"众数：",statistics.mode(l)) #带模块众数求法：np.argmax（l）

#-------------------------------------------不调用模块--------------------------------------------
#求中位数和众数
# l.sort()  #中位数在排序后进行查找
# mid = int(len(l) / 2)
# if len(l) % 2 == 0:
#     median = (l[mid-1] + l[mid]) / 2.0  #此处为mid-1，数组从l[0]开始
# else:
#     median = l[mid]
# print("中位数为:%f" % median)
#------------------------------------------------------------------------------------------------

import numpy as np

#求标准差
l_std = np.std(l,ddof=1)  #std()是计算标准差的函数，使用时要额外注意ddof这个参数：
# 在ddof = 1时，计算的是样本标准差，标准差公式根号内除以 （n-1）。在ddof = 0时，标准差公式根号内除以 n。
print("标准差为:%f" % l_std)


# 求整体方差（n）
var = np.var(l)
print("总体方差:",var)
#求样本方差（n-1）
# sample_var = np.var(l, ddof=1)
# print("样本方差:",sample_var)

#求四分位数
#求25%分位数：
print("1/4位数：",np.percentile(l,25))
#求75%分位数：
print("3/4位数：",np.percentile(l,75))

　　

 

 

 

 

 

2.已知某班50名学生的身高(单位为cm)数据如下;

158,162,169,165,151,160,161,158,172,149,168,158,165,166,158,163,159,168,170,168,155,162,171,153,153,159,163,165,162,164,156,170,166,159,164,171,168,168,164,166,168,160,154,157,155,164,163,156,159,164。

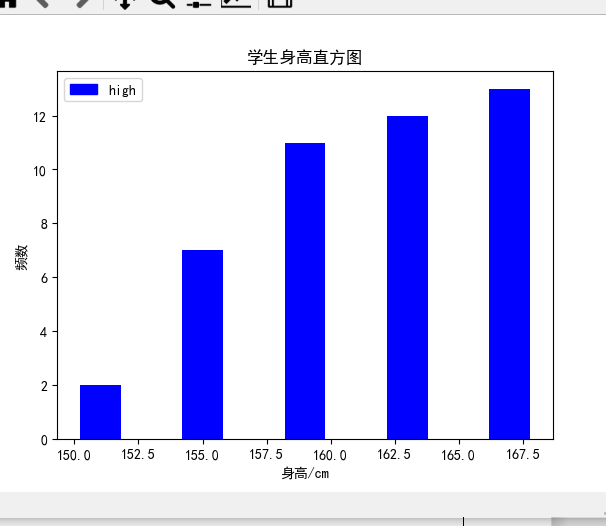
根据所给的数据画出直方图。

#直方图的绘制
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False# 防止字符无法显示
population_high=[158,162,169,165,151,160,161,158,172,149,168,158,165,166,
                 158,163,159,168,170,168,155,162,171,153,153,159,163,165,162,
                 164,156,170,166,159,164,171,168,168,164,166,168,160,154,157,155,164,163,156,159,164]
bins=[149,153,157,161,165,169]#包含下限值，不含上限值。
plt.hist(population_high,bins,histtype='bar',rwidth=0.4,color='b')
plt.xlabel('身高/cm')
plt.ylabel('频数')
plt.title('学生身高直方图')
blue_patch = mpatches.Patch(color='blue',label='high')
plt.legend(handles=[blue_patch])
plt.show()

　

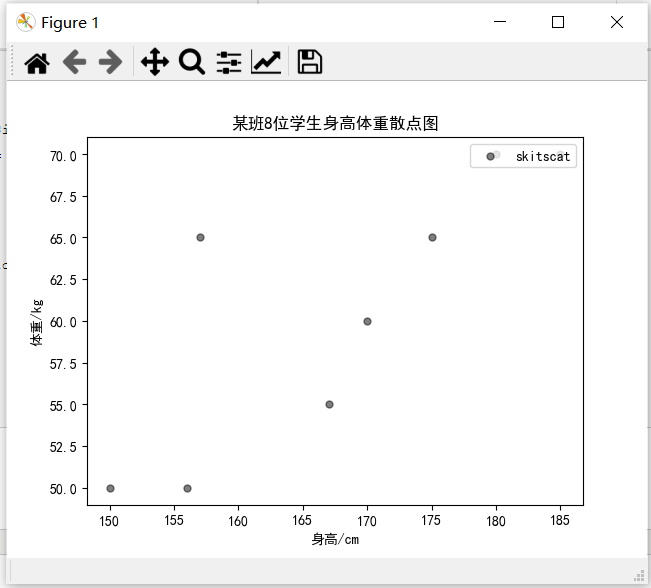
3.某班8位学生的身高和体重如下表所示,求散点图。

学生	身高/cm	体重/kg
A	167	55
B	156	50
C	185	70
D	175	65
E	180	70
F	150	50

#求散点图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False# 防止字符无法显示

x=[167,156,185,175,180,150,170,157]
y=[55,50,70,65,70,50,60,65]
plt.scatter(x,y,label='skitscat',color='k',s=25,marker='o',alpha=0.5)
plt.xlabel('身高/cm')
plt.ylabel('体重/kg')
plt.title('某班8位学生身高体重散点图')
plt.legend(loc=1)
plt.show()

　　

 

 

 

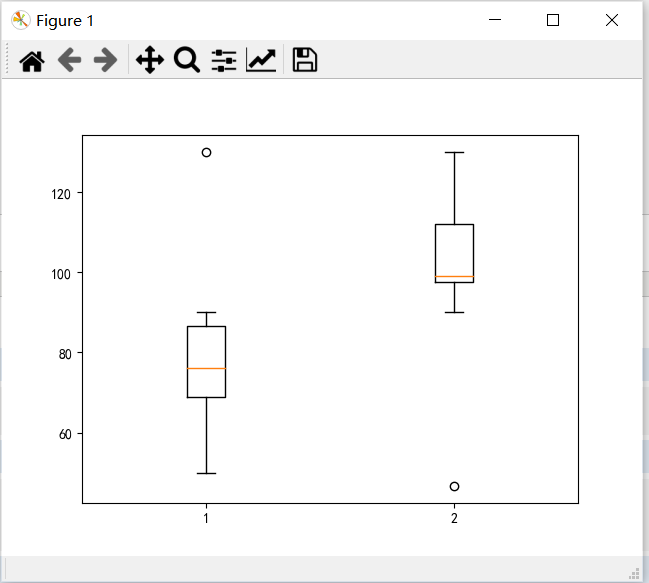
  4、假设西安市在岗工作人员年薪值如下(以千元为单位):

     {50,51,67,70.72,72,76,80,83,90,90,130}北京市在岗工作人员年薪值如下:(以千元为单位):{46.71 ,90,97,98,99,99,100,109,115,120,130}。求箱形图。

 

import matplotlib.pyplot  as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False# 防止字符无法显示
fig1,ax1=plt.subplots()
data1=[50,51,67,70.72,72,76,80,83,90,90,130]
data2=[46.71 ,90,97,98,99,99,100,109,115,120,130]
data=[data1,data2]
ax1.boxplot(data)
plt.show()