CF519E A and B and Lecture Rooms

 

 

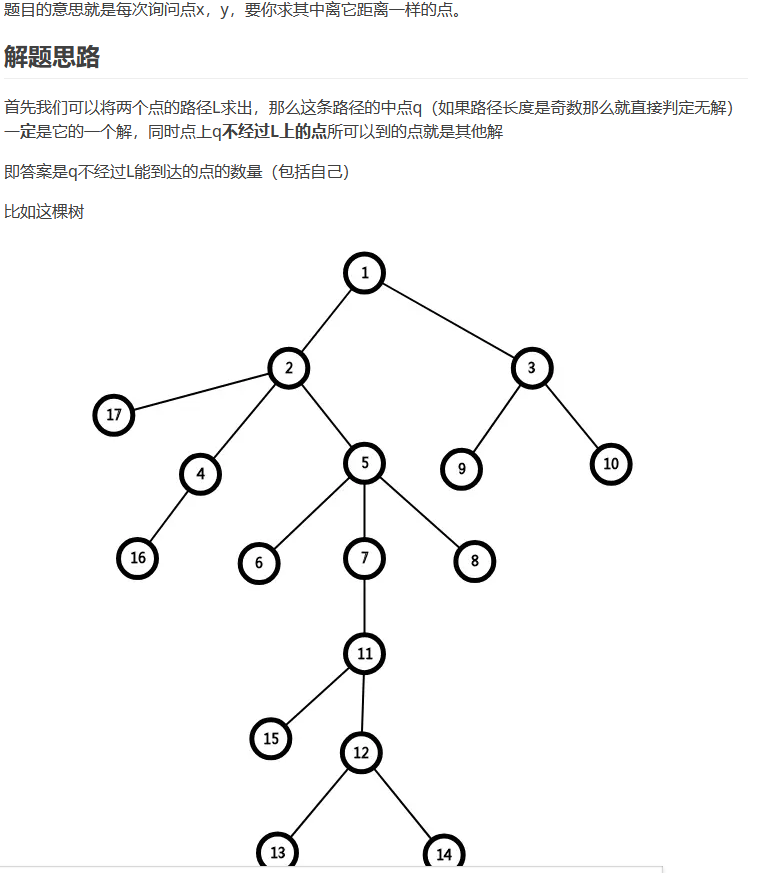
>>>不在x->y路径上的 mid point 的旁生点

>>>1. mid point == LCA -> siz[1]-siz[LCA->x]-siz[LCA->y] -> dep[x]==xep[y]

>>>2. mp!=LCA ->先到LCA再计算 siz[mp]-siz[mp->x] (mp dep 易求->dep[LCA]-()>>1  从x向上遍历 根据深度判断)

>>>因为 树  每一个点的 rd==1 所以其 f[][]即 父节点 唯一  向上遍历的路径唯一  否则形成环（rt -fa1-fa2）

:::二进制 无限分割 !=  >= > 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<bits/stdc++.h>
#define ll long long
#define ddd printf("-----------------debug\n");
using namespace std;
const int maxn=1e5+10;

int dep[maxn],f[maxn][20],siz[maxn];
int head[maxn],to[maxn<<1],nxt[maxn<<1],tot;
int n,m;

void add(int u,int v){
    to[++tot]=v; nxt[tot]=head[u]; head[u]=tot;
}

void dfs(int x,int fa)
{
    f[x][0]=fa;dep[x]=dep[fa]+1; siz[x]=1;
    for(int i=1;i<=18;i++) f[x][i]=f[f[x][i-1]][i-1];
    for(int i=head[x];i;i=nxt[i]){
        int v=to[i]; if(v==fa) continue;
        dfs(v,x);
        siz[x]+=siz[v];
    }
}
void get_ans(int x,int y)
{
    if(x==y){
        cout<<siz[1]<<'\n';
        return;
    }
    if(dep[x]==dep[y]){//mid point -> LCA
        for(int i=18;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
        cout<<siz[1]-siz[x]-siz[y]<<'\n';
        return;
    }
    if(dep[x]<dep[y]) swap(x,y);
    if((dep[x]-dep[y])%2==1) { cout<<"0"<<'\n'; return;}
    ///// mid point
    int d=(dep[x]-dep[y])>>1,x1=x;
    
    for(int i=18;i>=0;i--)
    {
        if(dep[f[x][i]]>=dep[y]) x=f[x][i];
        if(x==y){
            d=d+dep[x];
            for(int j=18;j>=0;j--) if(dep[f[x1][j]]>d) x1=f[x1][j];//tree each point rd==1
            cout<<siz[f[x1][0]]-siz[x1]<<'\n'; return;
        }
    }
    for(int i=18;i>=0;i--)
    {
        if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    }
    d=dep[x]-1+d;//dep==mid point
    for(int i=18;i>=0;i--) if(dep[f[x1][i]]>d) x1=f[x1][i];
        cout<<siz[f[x1][0]]-siz[x1]<<'\n'; 
    
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0);
    cin>>n;
    for(int i=1;i<=n-1;i++){
        int u,v; cin>>u>>v; add(u,v); add(v,u);
    }
    dfs(1,1);
    cin>>m;
    for(int i=1;i<=m;i++){
        int x,y; cin>>x>>y;
        get_ans(x,y);
    }
    return 0;
}