P1099 [NOIP2007 提高组] 树网的核

https://www.luogu.com.cn/problem/solution/P1099

无根树!!!!!

引理 1：对于一棵所有边权均为正的树，如果其存在多条直径，则树上必存在一点 pp，使得所有直径均经过该点（简单来说，所有直径必交于至少一点）。

证明：用反证法。

d1=max⁡{P(s,a),P(a,t)}d1​=max{P(s,a),P(a,t)}，d2=max⁡{P(s′,b),P(b,t′)}d2​=max{P(s′,b),P(b,t′)}，

即 d1,d2,P(a,b)d1​,d2​,P(a,b) 这三段拼接成了一条比 D(s,t),D(s′,t′)D(s,t),D(s′,t′) 这两条直径更长的简单路径，出现了矛盾。□□

定理 1：对于一棵所有边权均为正的树，如果其存在多条直径，则各直径的中点（不一定恰好是某个节点，可能在某条边的内部）是唯一的。

有三条直径两两相交，但不交于一点的情况？画图后马上就发现有环了。

引理 2.1：若两条直径有重叠的部分，则于重叠部分同一端点引出的两条直径的非重叠的部分的长度相等。

引理 2.2：若路径存在不位于直径上的部分，这条路径对应的偏心距一定不会比全部位于直径上的路径的偏心距的最小值更小。

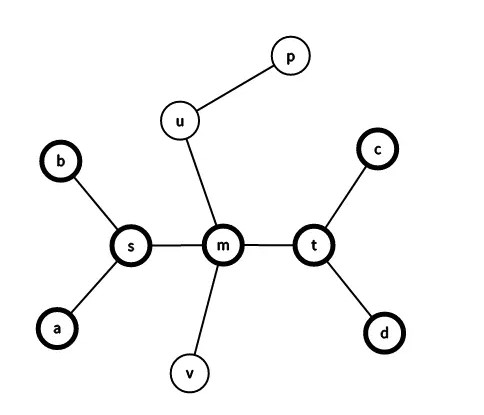
(只能是这样的形状 or 矛盾)

现在开始讨论。

1. 考虑 P(p,u)P(p,u) 这条路径。距离 P(p,u)P(p,u) 最远的点是哪个点，是 vv 吗？因为，P(b,m)+P(m,v)<P(b,m)+P(m,d)=D(b,d)P(b,m)+P(m,v)<P(b,m)+P(m,d)=D(b,d)，即 P(m,v)<P(m,d)P(m,v)<P(m,d)，因此距离 uu 最远的点，是直径的端点，不是 vv 这样一个不在直径上的点。
2. 现在考虑 P(u,v)P(u,v) 这条路径。距离 P(u,v)P(u,v) 最远的点是哪个点，是 pp 吗？如果 P(p,u)≥P(a,m)P(p,u)≥P(a,m)（其余情况同理），则 D(a,c)=P(a,m)+P(m,c)≤P(p,u)+P(m,c)<P(p,u)+P(u,m)+P(m,c)=P(p,c)D(a,c)=P(a,m)+P(m,c)≤P(p,u)+P(m,c)<P(p,u)+P(u,m)+P(m,c)=P(p,c)，与 D(a,c)D(a,c) 是直径矛盾。因此距离 P(u,v)P(u,v) 最远的点，仍然是直径的端点。
3. 最后考虑 P(m,m)P(m,m) 这条路径。距离 P(m,m)P(m,m) 最远的点是哪个点，是 pp 或者 vv 吗？注意到 p,vp,v 均不在直径上，于是 P(b,m)+P(m,p)<P(b,m)+P(m,d)=D(b,d)P(b,m)+P(m,p)<P(b,m)+P(m,d)=D(b,d)，即 P(m,p)<P(m,d)P(m,p)<P(m,d)（这里只举了 pp 的情况，vv 同理），因此距离 P(m,m)P(m,m) 最远的点，仍然是直径的端点

　>>一条链的偏心距    0-0-0-0//////-0-0--000 一定在 两侧 或链上的树  否则与直径矛盾

　　而两侧的ECC一定小于 只能够上 的最远距 -> 链上的树 预处理  max   但双指针是 max+min

/*
5 2
1 2 5
2 3 2
2 4 4
2 5 3

5

8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3

5
*/
//为什么要再求一边 每个知道 距离 

//无根树 的fa 唯一


#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<bits/stdc++.h>
#define ll long long
#define ddd printf("-----------------debug\n");
using namespace std;
const int maxn=310;


int n,s,head[maxn],cnt,dis[maxn<<1],k,mark[maxn<<1],fa[maxn<<1],ans=0x3f3f3f3f;
struct edge
{
    int to,w,nxt;
}e[maxn<<2];
void add(int u,int v,int w)
{
    e[++cnt]=(edge){v,w,head[u]};
    head[u]=cnt;
}
void dfs(int x,int faa)
{
    fa[x]=faa;
    if(dis[x]>dis[k]) k=x;
    for(int i=head[x]; i; i=e[i].nxt)
    {
        int v=e[i].to; 
        if(v==faa||mark[v]) continue;
        dis[v]=dis[x]+e[i].w;
        dfs(v,x);
    }
}

void dfs2(int x,int faa)
{
    fa[x]=faa;
   // if(dis[x]>dis[k]) k=x;
    for(int i=head[x]; i; i=e[i].nxt)
    {
        int v=e[i].to; 
        if(v==faa||mark[v]) continue;
        dis[v]=dis[x]+e[i].w;
        dfs(v,x);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>s;
    for(int i=1;i<=n;i++)
    {
        int x,y,v;
        cin>>x>>y>>v;
        add(x,y,v);add(y,x,v);
    }
    dis[1]=0; dfs(1,0);//!!!!!!!!!!!!!!!!!!!求的是差值
    dis[k]=0; dfs(k,0);//end -> start
    
    int top=k,tmp=0;
    for(int i=top,j=top; i; i=fa[i])
    {
        while(dis[j]-dis[i]>s) j=fa[j];//!!!!!!!!!!!!
        tmp=max( dis[top]-dis[j],dis[i] );//
        ans=min(ans,tmp);
    }
    for(int i=top; i; i=fa[i]) mark[i]=1;
    ////
    for(int i=top; i ;i=fa[i])
    {
       // k=i; 
        dis[i]=0; dfs2(i,fa[i]);//
    }
    for(int i=1;i<=n;i++)
        ans=max(ans,dis[i]);   
    
    cout<<ans<<endl;
    
    
    return 0;
}

 

 

 

 

-----------------------------------------