树状数组
如图所示,将一颗树向右倾斜就得到了一个树状数组,\(A[i]\)代表原数组\(C[i]\)代表树状数组。
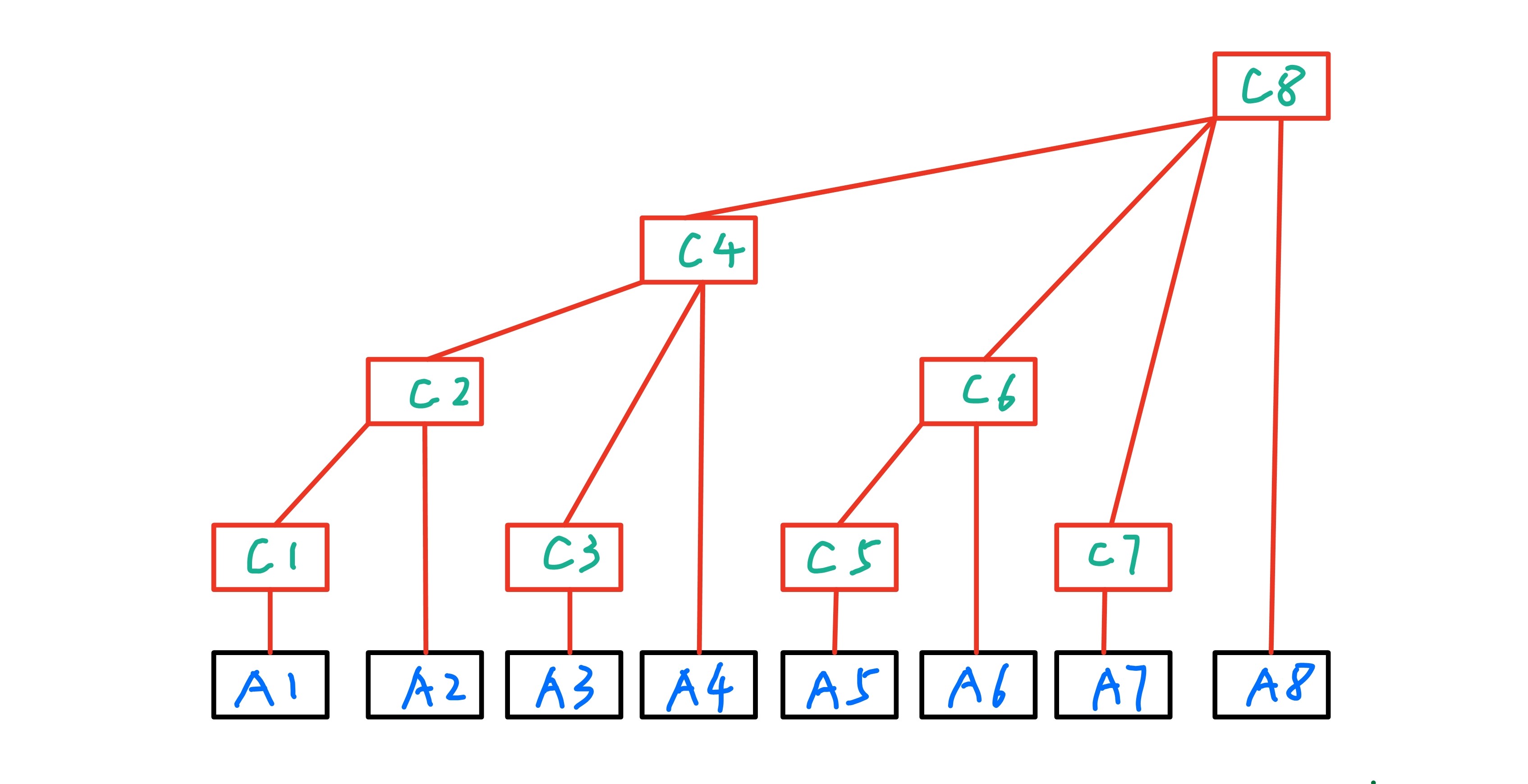
而每一个树状数组节点存的是子节点的和:
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
规律:
-
\(C[i] = A[i-2^k+1]+A[i-2^k+2]+...+A[i]\)(\(k\)为\(i\)二进制中从低位到高位连续0的长度)
-
\(SUM_i=C[i]+C[i-2^{k1}]+C[(i-2^{k1})-2^{k2}]+...\)(\(SUM_i\)为\(1-i\)的区间和;\(k1,k2...\)为上一项\([ ]\)内的二进制从低位到高位连续0的长度)
-
\(A[i]\)包含于\(C[i],C[i+2^{k1}],C[(i+2^{k1})+2^{k2}]...\)
\(2^k\)的求法
拿规律第一条来看:\(2^k=i\)&\((-i)\)
对于\(i\)&\((-i)\)可以自行举例当\(i=0\),奇数和偶数(可分为\(2^m\),不可分为\(2^m\))的情况理解。
最后可以得出得出结论:
1.\(i=0\)时\(i\)&\((-i)=0\)
2.\(i\)为奇数时\(i\)&\((-i)=1\)
3.\(i\)为偶数时\(i\)&\((-i)\)为\(i\)中2的最大次方因子
这里把\(2^k\)称为lowbit
单点修改,单点查询
下面是根据上面的性质写出的构造树状数组代码:
int n;//需要维护的区间总长度
int a[1000],c[1000];//原数组,树状数组
int lowbit(int i)//求lowbit
{
return i & (-i);
}
void update(int i, int x)//在i的位置加上x并更新树状数组,也可以用来初始化树状数组
{
while (i <= n)
{
c[i] += x;
i += lowbit(i);
}
}
int getsum(int i)//求1-i区间的和
{
int ans = 0;
while (i > 0)
{
ans += c[i];
i -= lowbit(i);
}
return ans;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)//初始化树状数组
{
cin >> a[i];
update(i, a[i]);
}
int t, x;//要修改的点和值
cin >> t >> x;
update(t, x);
int l, r;//求区间[l,r]的和
cin >> l >> r;
cout << getsum(r)-getsum(l-1) << endl;
return 0;
}
如果要求区间\([l,r]\)的和就通过前缀和相减:\(sum[r]-sum[l-1]\)即可求出。
区间修改,单点查询
这里就不能用上面的方法更新\([l.r]\)之间的所有值了,因为对时间的消耗太大了。
所以这就要引入差分数组,具体可以看前缀和和差分数组。
这里树状数组里面存的就都是差分数组了。
int n;//需要维护的区间总长度
int a[1000],c[1000];//原数组,差分树状数组
int lowbit(int i)//求lowbit
{
return i & (-i);
}
void update(int i, int x)//在i的位置加上x并更新差分树状数组,也可以用来初始化差分树状数组
{
while (i <= n)
{
c[i] += x;
i += lowbit(i);
}
}
int getsum(int i)//求A[i]的值
{
int ans = 0;
while (i > 0)
{
ans += c[i];
i -= lowbit(i);
}
return ans;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)//初始化差分树状数组
{
cin >> a[i];
update(i, a[i]-a[i-1]);//更新进树状数组的差分数组
}
int l,r, x;//要修改的区间和值
cin >> l>>r >> x;
update(l, x);//在差分数组l位置+k
update(r + 1, -x);//在差分数组r+1的位置-k
int t;
cin >> t;//输入查询的点的坐标
cout << getsum(t) << endl;
return 0;
}
区间修改,区间查询
还是利用差分法。
\(A[i]\)为原数组,\(D[i]\)为差分数组。
\(A[1]+A[2]+...+A[n]\)
\(=(D[1])+(D[1]+D[2])+...+(D[1]+D[2]+...+D[n])\)
\(=n*D[1]+(n-1)D[2]+...+D[n]\)
\(=n*(D[1]+D[2]+...+D[n])-(0*D[1]+1*D[2]+...+(n-1)*D[n])\)
所以可以得到下面公式:
所以接下来维护\(sum1[i]=D[i]\)和\(sum2[i]=(i-1)*D[i]\)两个树状数组就可以了。
int a[1000];//原数组
int sum1[1000], sum2[1000];//两个差分树状数组
int n;//需要维护的区间
int lowbit(int i)//求lowbit
{
return i & (-i);
}
void update(int i, int x)//更新树状数组
{
int k = i;//将i的值存储下来
while (i <= n)
{
sum1[i] += x;
sum2[i] += (k - 1)*x;
i += lowbit(i);
}
}
int getsum(int i)//求1-i区间的和
{
int ans = 0, k = i;
while (i > 0)
{
ans += k * sum1[i] - sum2[i];//按照上面的公式
i -= lowbit(i);
}
return ans;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)//初始化差分树状数组
{
cin >> a[i];
update(i, a[i]-a[i-1]);//更新进树状数组的差分数组
}
int l,r, x;//要修改的区间和值
cin >> l>>r >> x;
update(l, x);//在差分数组l位置+k
update(r + 1, -x);//在差分数组r+1的位置-k
cin >> l >> r;//输入查询的区间
cout << getsum(r)-getsum(l-1) << endl;//前缀和查区间
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号