CSP复赛训练7(2023.10.11)

T1

实际上可以做到 \(n\leq 10^7\)...

先打个暴力找规律

考虑构造：对于 \(n\leq 4\) 的，很显然自己手玩一下就发现答案不会超过 \(2\)。然后再大一点，然后你发现至少要 \(3\) 的答案，这是由于同时有了更多可以被限制的质数。\(n\ge 8\)，这时答案至少为 \(4\)。这时候就会有 \(2,3,5,7\) 这 \(4\) 个质数需要被筛选，于是你发现可以将每 \(4\) 个数构造成 \(1\) 个周期，因为没有任何一个质数 \(\equiv 0 \pmod 4\)。于是愉快做完。

T2

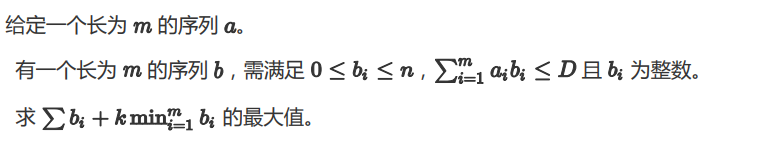
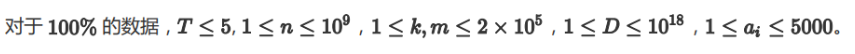
假如我们现在钦定了最小值，很明显，我们一定贪心的往 \(a_i\) 最小的那里加 \(b_i\) 能加则加，再考虑次小...容易证明，这一定会使得贡献最大化。

但是你真的枚举肯定不行，于是思考一下上面的玩意的性质。发现貌似是个峰值函数？二分一下做完了？

T3

\(n,m,k\leq 3\times 10^5\)。

sb 题。直接主席树维护从当前节点到根 \(dep_i-i\) 信息正反两遍，询问还可以做到在线，时间复杂度 \(O(n\log n)\)。好像还有树上差分的做法，可以做到 \(O(n)\) 离线。

T4

\(n,m\leq 2\times 10^5\)。

先来考虑无修改：
先预处理出每一个位置的数下一次出现位置 \(nxt_i\)，然后假如区间左端点为 \(i\)，那么其最大无重区间的右端点 \(r_i\) 则为 \(\min\limits_{j\ge i}nxt_j\)。

那么对于每个询问 \([L,R]\) 的答案就是 \(\sum\limits_{i=L}^R \min(r_i,R+1)-i\)，把常数项提出，变成求 \(\sum\limits_{i=L}^R \min(r_i,R+1)\)。思考如何快速维护这玩意。

由于后缀取 \(\min\) 的缘故，那么 \(r_i\) 满足单调不降。

考虑把整个 \(nxt\) 序列放到线段树上去维护，我们要的 \(r\) 就是要维护一个后缀形式取 \(\min\) 的玩意。我们现在看对于每个 \(nxt_i\) 可以贡献给哪些位置的 \(r_i\)，显然是他前面一段以 \(i\) 为结尾后缀取 \(\min\) 大于他的数（\(\Delta\)）。由于单调性，这可以线段树二分。

那我们现在考虑一个限制 \(lim\)，这个限制可以贡献给那些位置。我们再维护一个区间 \(\min\) 值 \(mi\)，然后考虑如何计算区间答案？如果右区间 \(mi>lim\) 那么整个右区间都得取 \(lim\)，递归求解左区间。如果右区间 \(mi\leq lim\)，则整个左区间都可以取自己的值，那么递归右区间。

我们这样做完后，算出的区间贡献相当于从当前区间右端点开始的后缀 \(\min\) 贡献，那区间之间则有右区间的 \(mi\) 可以更新 \(lim\) 从而对左区间贡献（\(\Delta\)）。带修也很简单，直接在树上改就行了。

最后的时间复杂度 \(O(n\log^2 n)\)。

Code

#include<bits/stdc++.h>
#define il inline 
#define rint register int
#define int long long
using namespace std;
const int N=2e5+10,INF=2147483647;
char *p1,*p2,buf[N];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
#define gc() getchar()
il int rd(){
	int x=0,f=1;
	char ch=gc();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=gc();}
	while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^48),ch=gc();
	return x*f;
}
int n,m;
int a[N];
struct Seg_tree{
	int mi,w;
}tr[N<<2];
int merge(int k,int l,int r,int lim){
	if(l==r)return min(tr[k].w,lim);
	int mid=(l+r)>>1;
	if(tr[k<<1|1].mi<=lim)return tr[k].w-tr[k<<1|1].w+merge(k<<1|1,mid+1,r,lim);
	else return merge(k<<1,l,mid,lim)+(r-mid)*lim;
}
void push_up(int k,int l,int r){
	tr[k].mi=min(tr[k<<1].mi,tr[k<<1|1].mi);
	int mid=(l+r)>>1;
	tr[k].w=merge(k<<1,l,mid,tr[k<<1|1].mi)+tr[k<<1|1].w;
}
int nxt[N];
set<int>pos[N];
void build(int k,int l,int r){
	if(l==r){
		tr[k].mi=tr[k].w=nxt[l];
		return;
	}
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	push_up(k,l,r);
}
void modify(int k,int l,int r,int L,int val){
	if(l==r){
		tr[k].mi=tr[k].w=val;
		return;
	}
	int mid=(l+r)>>1;
	if(L<=mid)modify(k<<1,l,mid,L,val);
	else modify(k<<1|1,mid+1,r,L,val);
	push_up(k,l,r);
}
int ans,lim;
void query(int k,int l,int r,int L,int R){
	if(l>=L&&r<=R){
		ans+=merge(k,l,r,lim);
		lim=min(lim,tr[k].mi);
		return;
	}
	int mid=(l+r)>>1;
	if(R>mid)query(k<<1|1,mid+1,r,L,R);
	if(L<=mid)query(k<<1,l,mid,L,R);
}
void Main(){
	n=rd(),m=rd();
	for(int i=1; i<=n; ++i)a[i]=rd(),pos[i].insert(n+1);
	for(int i=n; i>=1; --i){
		nxt[i]=*(pos[a[i]].begin());
		pos[a[i]].insert(i);
	}
	build(1,1,n);
	int op,x,y;
	set<int>::iterator it;
	while(m--){
		op=rd(),x=rd(),y=rd();
		if(op==1){
			it=pos[a[x]].find(x);
			int ne=*(++it);
			--it;
			if(it!=pos[a[x]].begin()){--it;modify(1,1,n,*it,ne);}
			pos[a[x]].erase(x);
			it=pos[y].lower_bound(x),a[x]=y;
			modify(1,1,n,x,*it);
			if(it!=pos[y].begin())--it,modify(1,1,n,*it,x);
			pos[y].insert(x);
		}else{
			ans=0;lim=y+1;
			query(1,1,n,x,y);
			ans-=(x+y)*(y-x+1)/2;
			printf("%lld\n",ans);
		}
	}
}
signed main(){
	freopen("team.in","r",stdin);
	freopen("team.out","w",stdout);
	int T=1;
	while(T--)Main();
	return 0;
}
/*
  4 3
  1 1 2 1
  2 1 3
  1 2 3
  2 1 4
 */