三、微分中值定理与导数的应用

3.1 微分中值定理

• 对于证明同一函数在不同点值的不等式可用拉格朗日中值定理

• 费马引理

  设函数 \(f(x)\) 在点 \(x_0\) 的某邻域 \(U(x_0)\) 内有定义，并且在 \(x_0\) 处可导，如果对任意的 \(x\in U(x_0)\) 有 \(f(x)\leq f(x_0)\) （或 \(f(x)\geq f(x_0)\)），那么 \(f'(x_0)=0\)

  （通常称导数为零的点为“驻点”）

  • 本定理本质上就是可导条件下极值点的必要条件

• 罗尔定理
  若函数 \(f(x)\) 满足：
  (1) 在闭区间 [a,b] 上连续
  (2) 在开区间 (a,b) 内可导
  (3) 在区间断点处的函数值相等，即 \(f(a)=f(b)\)
  则在 (a,b) 内至少有一点 \(\xi\) 使得 \(f'(\xi)=0\)

  • 罗尔定理中的 \(\xi\) 实际上就是 \(f(x)\) 的极值点
  • 罗尔定理也被用于证明“导函数的零点存在性问题”
  • 零点数量问题（至多有几个零点）证明，可用红书 P98 结论

• 拉格朗日中值定理
  若函数 \(f(x)\) 满足：
  (1) 在闭区间 [a,b] 上连续
  (2) 在开区间 (a,b) 内可导
  则在 (a,b) 内至少有一点 \(\xi\) 使等式 \(f(b)-f(a)=f'(\xi)(b-a)\) 成立，即 \(f'(\xi)=\dfrac{f(b)-f(a)}{b-a}\)
  设 \(x_0,x\) 是 \([a,b]\) 上任意两点，则至少存在一点 \(\xi\) ，使 \(f(x)=f(x_0)+f'(\xi)(x-x_0)\) 成立

• 有限增量定理

  在拉格朗日中值定理条件的区间 \([a,b]\) 内取 \(x\) 和 \(x+\Delta x\) 两点，则有：\(f(x+\Delta x)-f(x)=f'(x+\theta\Delta x)\cdot \Delta x\) 其中 \(0<\theta<1\)

  即 \(\Delta y = f'(x+\theta\Delta x)\cdot\Delta x \;,\; 0<\theta<1\) 该式称为有限增量公式（对比 \(\Delta y \approx dy\) ）

• 柯西中值定理
  若函数 \(f(x)\) 以及 \(F(x)\) 满足：
  (1) 在闭区间 [a,b] 上连续
  (2) 在开区间 (a,b) 内可导
  (3) 对任一 \(x \in (a,b),F'(x)\neq0\)
  则在 (a,b) 内至少有一点 \(\xi\) 使等式 \(\dfrac{f(b)-f(a)}{F(b)-F(a)}=\dfrac{f'(\xi)}{F'(\xi)}\) 成立

  • 注意：式中的两个 \(\xi\) 是同一个，因此柯西中值定理不能由两个函数的拉格朗日中值定理的合并所得，因为这样得到的两个函数的 \(\xi\) 不一定是同一个

3.2 洛必达法则

• 定理1

  (1) \(\lim_{x \to a}f(x)=\lim_{x \to a}g(x)=0\)（或 \(\infty\)）

  (2) 在点 a 的去心邻域内 \(f'(x),g'(x)\) 都存在且 \(g'(x)\neq 0\)

  (3) \(\lim_{x \to a}\dfrac{f'(x)}{g'(x)}\) 存在（或为无穷大）

  则 \(\lim_{x\to a}\dfrac{f(x)}{g(x)}=\lim_{x\to a}\dfrac{f'(x)}{g'(x)}\)

• 定理2

  (1) \(\lim_{x \to \infty}f(x)=\lim_{x \to \infty}g(x)=0\)（或 \(\infty\)）

  (2) 当 \(|x|>N\) 时 \(f'(x),g'(x)\) 都存在且 \(g'(x)\neq 0\)

  (3) \(\lim_{x \to \infty}\dfrac{f'(x)}{g'(x)}\) 存在（或为无穷大）

  则 \(\lim_{x\to \infty}\dfrac{f(x)}{g(x)}=\lim_{x\to \infty}\dfrac{f'(x)}{g'(x)}\)

• \(\lim_{x \to \infty}\dfrac{\log_ax}{x^\alpha}=0\) 、\(\lim_{x \to \infty}\dfrac{x^\alpha}{a^x}=0\) （\(\log_ax \ll x^\alpha \ll a^x\)）

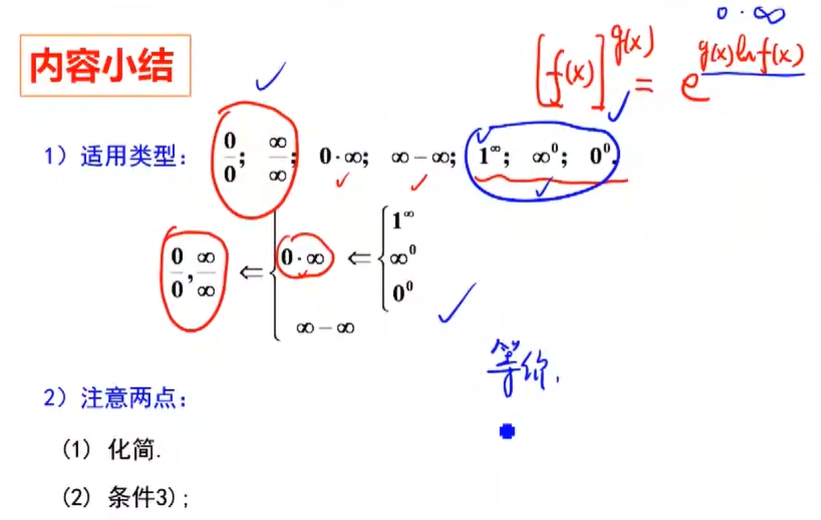
• 可以使用洛必达求解极限的特殊情况

  利用极限的非零因子的极限可先求取的性质，将复杂式的一部分通过洛必达先行求取

  形如 \(\lim \dfrac{f(x)}{g(x)}h(x)\) 的极限，其中 \(\dfrac{f(x)}{g(x)}\) 满足使用洛必达的条件，若洛必达后 \(\lim \dfrac{f(x)}{g(x)}=c\neq0\)（存在且不为 0），那么可作为极限非零因子提出，然后继续求解极限 \(c\lim h(x)\)

3.3 泰勒公式

• 注意： 近年真题经常出现利用带 Lagrange 余项的泰勒公式求解证明题

• 泰勒定理的本质是用多项式来逼近 \(f(x)\)，用已知点的信息表示未知点

  设多项式：\(P(x)=c_0+c_1(x-x_0)+c_2(x-x_0)^2+\cdots+c_n(x-x_0)^n\)

  令：\(P(x_0)=f(x_0)\)、\(P'(x_0)=f'(x_0)\)、\(P''(x_0)=f''(x_0)\)、······、\(P^{(n)}(x_0)=f^{(n)}(x_0)\)

  最终得到的 \(P_n(x)\) 可以以 \(o((x-x_0)^n)\) 的误差逼近 \(f(x)\)，即 \(f(x)=P_n(x)+o((x-x_0)^n)\)

• 带 Peano 余项的泰勒公式用于定性分析，适用于研究局部的问题，如极限、极值

• 带 Lagrange 余项的泰勒公式用于定理分析，适用于研究整体的问题，如最值，不等式等

• 带 Peano 余项的泰勒公式无法具体估算出误差大小，带 Lagrange 余项的泰勒公式可以

• 泰勒中值定理1（带 Peano 余项）

  若函数 \(f(x_0)\) 处 n 阶可导，则存在 \(x_0\) 的一邻域，对其中任一 \(x\) 有：

  \(f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n)\)

  其中 Peano 余项为 \(o((x-x_0)^n)\)

• 泰勒中值定理2（带拉格朗日余项）

  若函数 \(f(x_0)\) 处 n+1 阶可导，则存在 \(x_0\) 的一邻域，对其中任一 \(x\) 有：

  \(f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}\)

  其中拉格朗日余项为 \(\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}\)，式中 \(\xi\) 是 \(x_0\) 与 \(x\) 之间的某个值

  （当 \(n=0\) 时，上述公式变为拉格朗日中值公式，表明定理2为拉格朗日中值定理的推广）

• 泰勒中值定理中的余项是用泰勒多项式近似表达函数 \(f(x)\) 的误差

• 泰勒多项式：

  \(p_n(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n\) 称为函数在 \(x_0\) 处的 n 次泰勒多项式

• 麦克劳林公式（Maclaurin）：泰勒公式中取 \(x_0 = 0\) 所得式

  • 带 Peano 余项的麦克劳林公式：\(f(x)=f(0)+f'(0)x+\cdots+\dfrac{f^{(n)}(0)}{n!}x^n+o(x^n)\)

  • 带拉格朗日余项的麦克劳林公式：\(f(x)=f(0)+f'(0)x+\cdots+\dfrac{f^{(n)}(0)}{n!}x^n+\dfrac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1}\)

    其中 \(0<\theta<1\)

• 几个初等函数的 Maclaurin 公式（带拉格朗日余项的、带 Peano 余项的）

  • \(e^x=1+x+\dfrac{1}{2!}x^2+\cdots+\dfrac{1}{n!}x^n+\dfrac{x^{n+1}}{(n+1)!}e^{\theta x}\)
    • \(e^x=1+x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3+\dfrac{1}{4!}x^4+\dfrac{1}{5!}x^5+\dfrac{1}{6!}x^6+o(x^6)\)
  • \(\sin x=x-\dfrac{1}{3!}x^3+\cdots+(-1)^{n-1}\dfrac{x^{2n-1}}{(2n-1)!}+(-1)^n\dfrac{\cos \theta x}{(2n+1)!}x^{2n+1}\)
    • \(\sin x=x-\dfrac{1}{3!}x^3+\dfrac{1}{5!}x^5-\dfrac{1}{7!}x^7+o(x^7)\)
  • \(\cos x=1-\dfrac{1}{2!}x^2+\cdots+(-1)^n\dfrac{x^{2n}}{(2n)!}+ o(x^{2n})\)
    • \(\cos x=1-\dfrac{1}{2!}x^2+\dfrac{1}{4!}x^4-\dfrac{1}{6!}x^6+o(x^6)\)
    • 易记：\(\cos x=x^0-\dfrac{1}{2!}x^2+\dfrac{1}{4!}x^4-\dfrac{1}{6!}x^6+o(x^6)\)
  • \(\tan x=x+\dfrac{1}{3}x^3+\dfrac{2}{15}x^5+o(x^5)\)
  • \(\ln(1+x)=x-\dfrac{1}{2}x^2+\dfrac{1}{3}x^3-\dfrac{1}{4}x^4+\dfrac{1}{5}x^5-\dfrac{1}{6}x^6+o(x^6)\)

• 利用泰勒公式求极限的要点

  • 通常用于分式形式的极限
  • \(\lim_{x\to0}\dfrac{f(x)}{g(x)}\) 型可采用麦克劳林公式（带 Peano 余项）
  • \(\lim_{x\to0}\dfrac{f(x)}{g(x)}\) 型若对分子进行泰勒公式展开时，展开的阶数通常需要达到分母部分的 \(x\) 最高阶，即若 \(g(x)\) 中最高阶项为 \(x^k\)，应展开至 \(f(x)=f(0)+f'(0)x+\cdots+\dfrac{f^{(k)}(0)}{k!}x^k+o(x^k)\)

3.4 函数单调性与曲线凹凸性

• 对于需要通过导数的正负情况来判断函数单调性的证明，可尝试使用拉格朗日中值定理

• 复合函数的单调性（假设复合有意义）

  假设函数 \(f(x)\) 单增，\(g(x)\) 单减，则：

  • \(f[f(x)]\) 和 \(g[g(x)]\) 都单调增
  • \(f[g(x)]\) 和 \(g[f(x)]\) 都单调减

• 函数的凹凸性：

  • 凹：\(f(\dfrac{x_1+x_2}{2})<\dfrac{f(x_1)+f(x_2)}{2}\)
  • 凸：\(f(\dfrac{x_1+x_2}{2})>\dfrac{f(x_1)+f(x_2)}{2}\)

• 函数凹凸性与导数关系：

  • 若在 \((a,b)\) 内 \(f''(x)>0\)，则 \(f(x)\) 在 \([a,b]\) 上的图像是凹的
  • 若在 \((a,b)\) 内 \(f''(x)<0\)，则 \(f(x)\) 在 \([a,b]\) 上的图像是凸的

• 拐点： 函数的凹凸性发生变化的点，即函数二阶导数发生正负变化的点

  • 拐点的必要条件：若 \((x_0,y_0)\) 为拐点，则 有 \(f''(x_0)=0\)，反之不一定
  • 可能为拐点的情况：① \(f''(x_0)=0\) ；② \(f''(x_0)\) 不存在

• 拐点的第一充分条件（二阶导数左右异号的点）

  • 先求二阶导数所以零点 \(f''(x_i)=0\)
  • 观察判断 \(f''(x_i)\) 左右负号是否异号，异号则 \(x_i\) 为拐点
  • 再检查\(f''(x)\) 不存在的点（观察一阶导数上的不可导点）

• 拐点的第二充分条件（三阶可导，且二阶导数为零、三阶导数不为零）

3.5 函数的极值与最值

• 注意区分极值点和驻点：

  ① 导数为零的点称为驻点；② 极值点不一定是驻点（驻点要求该点可导）

• 可能为极值点的情况：① \(f'(x_0)=0\)；② \(f'(x_0)\) 不存在

• 极值的必要条件： 若 \(f(x)\) 在 \(x_0\) 处取得极值，则有 \(f'(x_0)=0\)

• 极值的第一充分条件：（可以判断导数不存在的点的情况）

  \(f(x)\) 在 \(x_0\) 连续且在该点某去心领域可导

  (1) 若 \(x_0\) 左邻域 \(f'(x)>0\)，右邻域 \(f'(x)<0\)，则 \(x_0\) 处取得极大值

  (2) 若 \(x_0\) 左邻域 \(f'(x)<0\)，右邻域 \(f'(x)>0\)，则 \(x_0\) 处取得极小值

  (3) 若 \(x_0\) 邻域内 \(f'(x)\) 符号不变，则 \(x_0\) 处取没有极值

• 极值的第二充分条件：

  \(f(x)\) 在 \(x_0\) 处具有二阶导数且 \(f'(x_0)=0\;,\;f''(x_0)\neq0\)

  (1) 当 \(f''(x_0)<0\)，在 \(x_0\) 处取得极大值

  (2) 当 \(f''(x_0)>0\)，在 \(x_0\) 处取得极小值

• 求函数最值的一般方法：（设要求闭区间 \([a,b]\) 内的最值）

  • 第一步：取得函数再开区间 \((a,b)\) 内的驻点（导数为0的点）、导数不存在的点
  • 第二步：求出函数在第一步中取得的点的函数值，和函数在区间端点 \(a,b\) 处的函数值
  • 第三步：比较第二步各点的函数值，然后取最值

• 极值与最值的关系

  • 当连续函数 \(f(x)\) 在 \([a,b]\) 内仅有唯一极值点，若为极大值点（或极小值点），则该点是 \(f(x)\) 在 \([a,b]\) 上个的最大值（或最小值）
  • 若 \(f(x)\) 在开区间 \((a,b)\) 上取得最值，则该最值点就是一个极值点

3.6 函数图形的描绘

• 利用导数描绘函数图形的一般步骤：

  (1) 确定函数 \(y=f(x)\) 定义域，并考察器奇偶性和周期性

  (2) 求导函数 \(f'(x),f''(x)\)，并求出 \(f'(x)\) 及 \(f''(x)\) 为 0 和不存在的点

  (3) 列表判别增减及凹凸区间，求初极值点和拐点

  (4) 求渐近线

  (5) 确定某些特殊点，描绘函数图形

• 曲线的渐近线

  (1) 若 \(\lim_{x\to\infty}f(x)=A\) （\(\lim_{x\to-\infty}f(x)=A\) 或 \(\lim_{x\to+\infty}f(x)=A\)）则 \(y=A\) 是曲线 \(y=f(x)\) 的水平渐近线

  (2) 若 \(\lim_{x\to x_0}f(x)=\infty\)，则 \(x=x_0\) 是 \(y=f(x)\) 的垂直渐近线

  (3) 若 \(\lim_{x\to\infty}\dfrac{f(x)}{x}=a\;,\; b=\lim_{x\to\infty}(f(x)-ax)\)，则 \(y=ax+b\) 是 \(y=f(x)\) 的斜渐近线

  • 若 \(\lim_{x\to\infty}[f(x)-(kx+b)]=0\)，则通常可得出 \(y=kx+b\) 为 \(f(x)\) 的斜渐近线
  • 注意斜渐近线可能不止一条（因为 \(\lim_{x\to-\infty}\dfrac{f(x)}{x}\) 和 \(\lim_{x\to+\infty}\dfrac{f(x)}{x}\) 结果可能不同）

3.7 曲率

• 弧微分公式：\(ds=\sqrt{1+y'^2}dx\)，即直角坐标系下的弧微分公式

• 曲率描述曲线的弯曲程度

• 曲率计算公式：\(K = \dfrac{|y''|}{(1+y'^2)^{\frac{3}{2}}}\) （注意，分子分母应统一求导对象，如分子是对 x 求导，分母的弧微分部分也得是对 x 求导，有时题目会给参数方程，此时要借助参数方程进行求导了）

• 圆上各点处的曲率相同，为半径 \(a\) 的倒数 \(\dfrac{1}{a}\)

• 曲率圆：以曲线某点切线作为圆的切线，在曲线凹侧以该点曲率倒数（\(\dfrac{1}{K}\)）作为半径作的圆