感知机到支持向量机1

1. 感知机

1.1 感知机是模拟神经元功能的一种数学模型

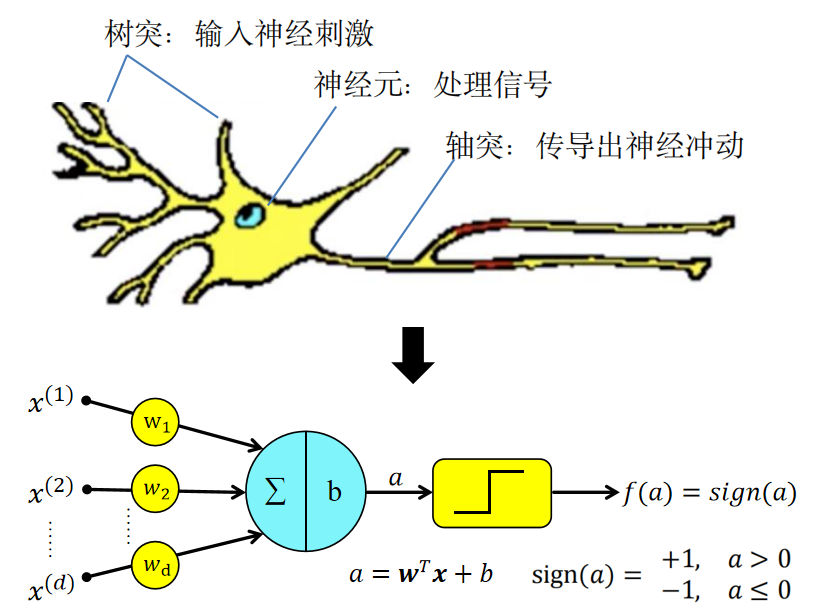
神经元细胞的工作机理：

多个树突所搜集到的输入信号经过神经元的集中处理，如果达到一定的激发阈值，就会激活轴突的输出。

感知机的模拟：

• 来自树突的输入信号向量：\(x=[x^{(1)},x^{(2)},\dots,x^{(d)}]\)

• 神经元集中处理

  • 权重向量 \(w = (w_1,w_2,\dots,w_d)\)
  • 调节信号向量各维度的贡献 \(w^Tx = \sum_i^d{w_ix^{(i)}}=w_1x^{(1)}+w_2x^{(2)}+\dots+w_dx^{(d)}\)

• 激活并输出

  • 激活输出可以表示为：\(out=\begin{cases}1,&w^Tx>\theta\\0,&w^Tx\leq\theta\end{cases}\) ，其中 \(\theta\) 为阈值
    • 为了简化计算和框架统一，引入偏置 \(b\) 代替传统的阈值，在此基础上使用不同的激活函数 \(f\) 进行激活
    • 于是 \(out=f(w^Tx+b)\)
  • 感知机使用阶跃函数激活：\(out=sign(w^Tx+b)=sign(a)=\begin{cases}+1,&a>0\\-1,&a\leq0\end{cases}\)

1.2 感知机是二分类的线性分类模型

感知机是用于二分类任务的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取 \(\pm1\) 二值。感知机对应于特征空间中，将实例线性划分为正负两类的分离超平面（决策超平面），感知机模型学习的目标就是求出这个决策超平面。

• 感知机对应的决策超平面：\(w^Tx+b=0\)
• 感知机的判别函数：\(G(x)=w^Tx+b\)
• 感知机模型：\(f(x)=sign(w^Tx+b)=\begin{cases}+1,&(w^Tx+b)>0\\-1,&(w^Tx+b)\leq0\end{cases}\)

几何解释：

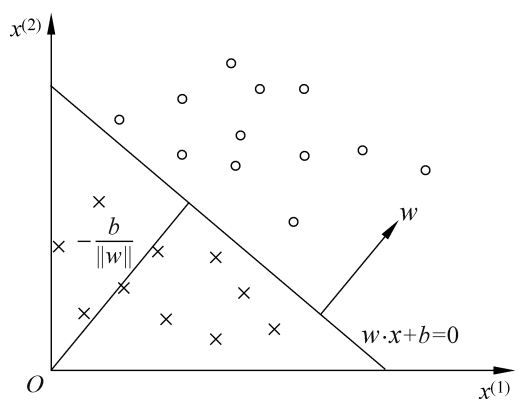
• 线性方程 \(w^Tx+b=0\) 对应于上图所示特征空间中，将两类样本分为两类的决策直线（高维特征空间称为决策超平面）
• 权重向量 \(w\) 为该决策超平面的法向量
• 特征空间中不同位置的样本在判别函数 \(G(x)=w^Tx+b\) 上的表现
  • 当样本在决策超平面法向量指向的一侧，\(w^Tx+b>0\)
  • 当样本在决策超平面法向量指向的另一侧，\(w^Tx+b<0\)
  • 当样本在决策超平面上，\(w^Tx+b=0\)

1.4 感知机的学习算法

1.4.1 数据集的线性可分性

定义：给定一个数据集
\(T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\},\;\;x_i\in\mathbb{R}^d,\;y\in\{+1,-1\},\;i=1,2,\dots,N\) ，如果存在一个超平面 \(S:w^Tx+b=0\) 能将数据集中的正负样本完全正确地划分到超平面两侧，即对所有 \(y_i=+1\) 的样本 \(x_i\) 有 \(w^Tx+b>0\)，对所有 \(y_i=-1\) 的样本 \(x_i\) 有 \(w^Tx+b<0\)，则称数据集 \(T\) 线性可分数据集。否则，称数据集 \(T\) 线性不可分。

1.4.2 感知机的学习目标

根据上述线性可分数据集的定义，可以将感知机的学习目标描述为：

利用给定的训练数据集，求得权向量 \(w\) 和偏置 \(b\)，使对应的决策超平面能将所有样本正确分类，即：

• 对所有 \(y_i=+1\) 的样本 \(x_i\) 有 \(w^Tx_i+b>0\)
• 对所有 \(y_i=-1\) 的样本 \(x_i\) 有 \(w^Tx_i+b<0\)

表明当 \(y_i\) 正负符号与 \(w^Tx_i+b>0\) 一致时样本被正确分类，于是上述描述等价于：

利用给定的训练数据集，求得权向量 \(w\) 和偏置 \(b\)，使所有样本满足 \(y_i(w^Tx_i+b)>0\)

1.4.3 感知机的学习策略

为了获取决策超平面的权向量 \(w\) 和偏置 \(b\)，需要制定学习策略：定义损失函数并将损失函数最小化

感知机算法最初没有明确定义一个损失函数，但其优化的目标是最小化误分类点的数量，可以利用如0-1损失作为损失函数，后来随支持向量机明确引入了间隔的概念，“样本到决策边界的距离”相关概念在机器学习中得到广泛应用和推广。

点到超平面的距离可以使用 \(w^Tx+b\) 进行测量，其符号是否与样本点符号一致可以表示分类是否正确，于是引出可以表示分类正确性和确信程度的函数间隔表式：\(\hat\gamma_i=y_i(w^Tx_i+b)\)，注意这里的函数间隔是针对各样本自身而言的。

（现代）感知机的损失函数选用误分类点到决策超平面的距离表示：\(L(w,b)=\sum_{x_i \in M}{-y_i(w^Tx_i + b)}\)，其中 \(M\) 为误分类样本集。

感知机使用梯度下降算法（SGD）对目标函数进行优化，每次（随机）选取一个误分类样本对应的损失计算梯度，利用梯度更新 \(w,b\) ：

• \(\nabla_wL(w,b) = \sum_{x_i \in M}{-y_ix_i}\)，第 \(i\) 个样本对应 \(w\) 的梯度为 \(-y_ix_i\)
• \(\nabla_bL(w,b) = \sum_{x_i \in M}{-y_i}\)，第 \(i\) 个样本对应 \(b\) 的梯度为 \(-y_i\)
• 随机选取一个误分类点 \((x_i,y_i)\) 更新 \(w,b\)：
  • \(w^+ \longleftarrow w - \eta(-y_ix_i) = w + \eta y_ix_i\)
  • \(b^+ \longleftarrow b - (-y_i) = b + \eta y_i\)
• 这次更新的总体效果是使决策边界更接近错误分类的样本 \((x_i,y_i)\)，并希望 \(w^+,b^+\) 现在更接近所有样本的决策边界

1.4.4 感知机学习算法

输入：训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\},\;\;x_i\in\mathbb{R}^d,\;y\in\{+1,-1\},\;i=1,2,\dots,N\) ；学习率 \(0<\eta\leq1\)

输出：\(w,b\) ；感知机模型 \(f(x) = sign(w^Tx+b)\)

(1) 初始化 \(w_0,b_0\)

(2) 训练集随机选取数据 \((x_i,y_i)\)

(3) 若 \(y_i(w^Tx_i+b) \leq 0\) ：

​ \(\qquad w^+ \longleftarrow w + \eta y_ix_i\)

​ \(\qquad b^+ \longleftarrow b + \eta y_i\)

(4) 重复(2)和(3)直到没有误分类点

注意：

在代码实现过程中，常常是通过循环遍历乱序后的数据集实现SGD的，直到一次遍历结束都没有误分类点出现，则终止迭代。

在笔算过程中，是直接循环遍历数据集，直到一次遍历结束后都没有误分类，终止迭代。

1.5 感知机收敛性证明

Novikoff 定理表明，对于线性可分数据集，感知机经过有限次迭代可以得到一个将数据集样本完全正确划分的决策超平面，即前文所述的感知机的学习算法是收敛的。下面将对Novikoff 定理展开证明。

• 为了便于叙述与推导：

  • 令偏置并入权向量：\(\hat w = (w^T,b)^T\) ；相应的对样本进行维度拓展，为偏置引入系数计算：\(\hat x_i = (x_i^T, 1)^T\)

  • 损失函数变为 \(L(w,b)=\sum_{x_i \in M}{-y_i\hat{w}^T\hat{x_i}}\)

  • SGD更新参数：\(\hat{w}^+ \longleftarrow \hat{w} + \eta y_i\hat{x}_i\)

Novikoff 定理：

对于线性可分数据集 \(T=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\},\;\;x_i\in\mathbb{R}^{d+1},\;y\in\{+1,-1\},\;i=1,2,\dots,N\)

① 存在满足 \(||\hat{w}_{opt}||=1\) 的超平面 \(\hat{w}_{opt}^T\hat{x}=w_{opt}^Tx+b=0\) 能将数据集完全正确划分；且存在 \(\gamma > 0\)，满足：

\[y_i(\hat{w}_{opt}^T\hat{x}_i)=y_i(w_{opt}^Tx_i+b) \geq 0 \]

② 令 \(R=\max_{i=1\dots N}||\hat{x}_i||\)，则基于随机梯度下降更新的感知机算法在训练数据集 \(T\) 上的误分类次数 \(k\) 满足不等式：

\[k \leq (\dfrac{R}{\gamma})^2 \]

证 ①：

由于数据集线性可分，所以一定存在决策超平面 \(\hat{w}_{opt}^T\hat{x}=0\) 能将数据集样本完全正确划分；

由于缩放 \(||\hat{w}_{opt}||\) 相当于同时缩放权向量和偏置，所以不改变决策超平面位置，令 \(||\hat{w}_{opt}||=1\) ；

由于 \(y_i(\hat{w}_{opt}^T\hat{x}_i)>0,\;\;i=1\dots N\)，所以存在 \(\gamma = \min_i\{y_i(\hat{w}_{opt}^T\hat{x}_i)\}\) 使满足： \(y_i(\hat{w}_{opt}^T\hat{x}_i)\geq\gamma,\;\;i=1\dots N\)；

证毕。

证 ②：

设\(\hat{w}_0\) 是初始参数向量（为零向量），\(\hat{w}_k\) 是感知机训练过程第 \(k\) 次误分类更新得到的参数向量

所以有 \(\begin{cases}y_i(\hat{w}_{opt}\cdot\hat{x}_i)\leq0 &(a)\\ \hat{w}_k=\hat{w}_{k-1}+\eta y_i\hat{x}_i &(b)\end{cases}\)

由 ① 的 \(||\hat{w}_{opt}||=1\)：

\(\begin{aligned} \hat{w}_{opt} \cdot \hat{w}_k &= \hat{w}_{opt} \cdot \hat{w}_{k-1} + \eta y_i\hat{w}_{opt}\cdot\hat{x}_i \\ &\geq \hat{w}_{opt} \cdot \hat{w}_{k-1} + \eta\gamma \\ &\geq \hat{w}_{opt} \cdot \hat{w}_{k-2} + 2\eta\gamma \\ &\geq \cdots \\ &\geq\hat{w}_{opt} \cdot \hat{w}_0 + k\eta\gamma \\\end{aligned}\)

因为 \(\hat{w}_0\) 是零向量，所以 \(\hat{w}_{opt} \cdot \hat{w}_k \geq k\eta\gamma\)

根据柯西-施瓦茨不等式：\(\hat{w}_{opt} \cdot \hat{w}_k \leq ||\hat{w}_{opt}|| \cdot ||\hat{w}_k||=||\hat{w}_k||\)

对于 \(||\hat{w}_k||^2\)：

\(\begin{aligned} ||\hat{w}_k||^2 &= ||\hat{w}_{k-1}+\eta y_i\hat{x}_i||^2 \\ &= ||\hat{w}_{k-1}||^2 + 2\eta y_i(\hat{w}_{k-1}\cdot\hat{x}_i) + \eta^2y_i^2||\hat{x}_i||^2 \\ &\leq ||\hat{w}_{k-1}||^2 + \eta^2||\hat{x}_i||^2 \qquad \because y_i(\hat{w}_{k-1}\cdot\hat{x}_i)\leq0 \\ &\leq ||\hat{w}_{k-1}||^2 + \eta^2R^2 \qquad \because R=\max_i||\hat{x}_i|| \\ &\leq ||\hat{w}_{k-2}||^2 + 2\eta^2R^2 \\ &\leq \cdots \\ &\leq ||\hat{w}_0||^2 + k\eta^2R^2 \end{aligned}\)

因为 \(\hat{w}_0\) 是零向量，所以 \(||\hat{w}_k||^2 \leq k\eta^2R^2\)

于是有：\(k\eta\gamma \leq \hat{w}_{opt} \cdot \hat{w}_k \leq ||\hat{w}_k|| \leq \sqrt{k\eta^2R^2}\)

所以证得：\(k \leq (\dfrac{R}{\gamma})^2\)

1.6 补充

1.6.1 关于参数更新

为了更好理解感知机是如何随机梯度下降算法获取决策超平面的，下面通过可视化一次SGD参数更新的过程进行说明。

参数的更新包括对权向量 \(w\) 和偏置 \(b\) 的更新，权向量 \(w\) 实际为决策超平面的法向量，影响决策超平面的方向；偏置则影响决策超平面到原点的距离。

使用三个例子分别讨论 \(w\) 和 \(b\) 的更新对决策超平面产生的影响：

示例 ①（超平面方向不变）：

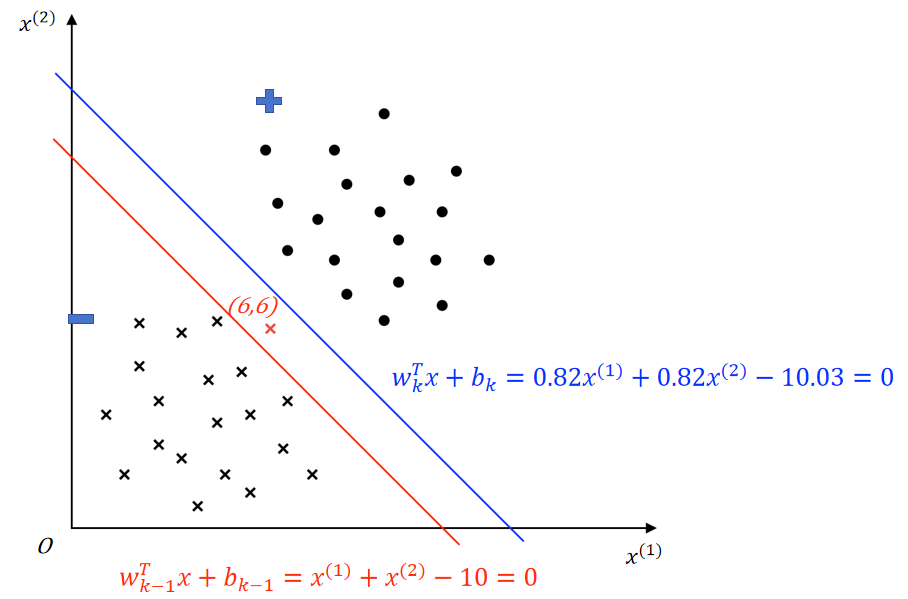
假设上图所示红色决策边界 \(w_{k-1}^Tx+b_{k-1}=x^{(1)}+x^{(2)}-10=0\) 由第 \(k-1\) 次误分类更新所得，随机梯度下降过程中，选取了上图被红色决策边界误分类的红色负样本进行参数更新。（红色负样本 \(x_e=(6,6),y_e=-1\)，\(y_e(w_{k-1}^Tx_e+b_{k-1})=-(6+6-10)<0\)，即误分类）

参数更新（\(\eta=0.03\)）：

• 更新权向量 \(w\)
  • \(w_k = w_{k-1} + \eta y_ex_e=(1,1)^T + 0.03*(-(6,6)^T)=(0.82,0.82)^T\)
• 更新偏置 \(b\)
  • \(b_k = b_{k-1} + \eta y_e=-10 + 0.03*(-1)=-10.03\)

得到蓝色决策边界 \(w_k^Tx+b_k=0.82x^{(1)}+0.82x^{(2)}-10.03=0\)

可以发现：

决策边界更新后，权向量由 \(w_{k-1} = (1,1)^T\) 调整为 \(w_k=(0.82,0.82)^T\)，表明更新后决策边界法向量方向没变，参考如下左图；

决策边界更新后，偏置由 \(b_{k-1}=-10\) 调整为 \(b_k=-10.03\)；以 \((0,0)\) 为原点，分别代入红、蓝决策边界方程求决策边界到原点的距离： \(d_{red}=\dfrac{|b_{k-1}|}{||w_{k-1}||} \approx 7.07\;,\;d_{blue}=\dfrac{|b_k|}{||w_k||} \approx 8.65\)，表明更新后决策边界远离了原点，参考如下右图。

---

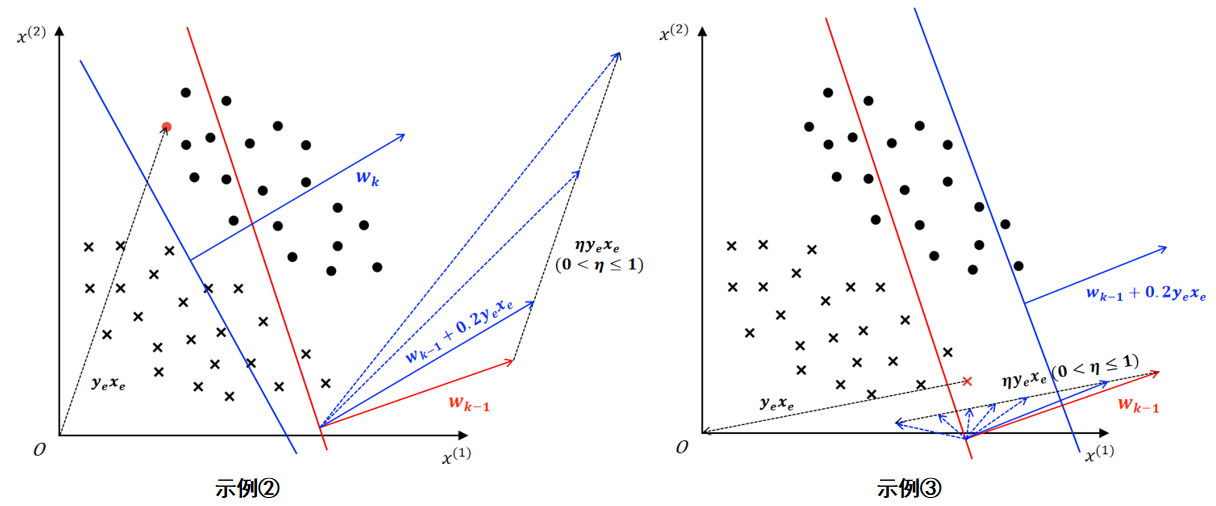
示例 ②：

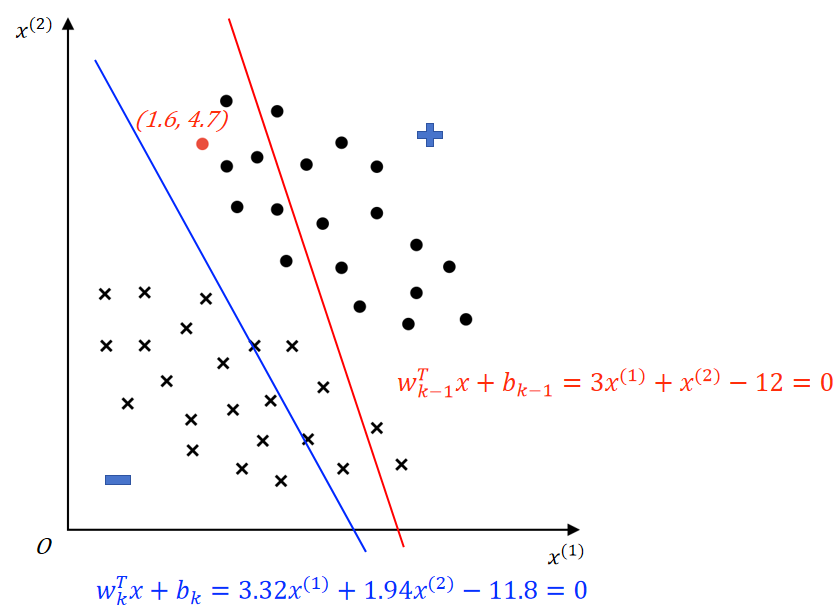
假设上图所示红色决策边界 \(w_{k-1}^Tx+b_{k-1}=3x^{(1)}+x^{(2)}-12=0\) 由第 \(k-1\) 次误分类更新所得，随机梯度下降过程中，选取了上图被红色决策边界误分类的红色正样本进行参数更新。（红色负样本 \(x_e=(1.6,4.7),y_e=+1\)，\(y_e(w_{k-1}^Tx_e+b_{k-1})=1*(3*1.6+4.7-12)<0\)，即误分类）

参数更新（\(\eta=0.2\)）：

• 更新权向量 \(w\)
  • \(w_k = w_{k-1} + \eta y_ex_e=(3,1)^T + 0.2*(1*(1.6,4.7)^T)=(3.32,1.94)^T\)
• 更新偏置 \(b\)
  • \(b_k = b_{k-1} + \eta y_e=-12 + 0.2*(1)=-11.8\)

得到蓝色决策边界 \(w_k^Tx+b_k=3.32x^{(1)}+1.94x^{(2)}-11.8=0\)

可以发现：

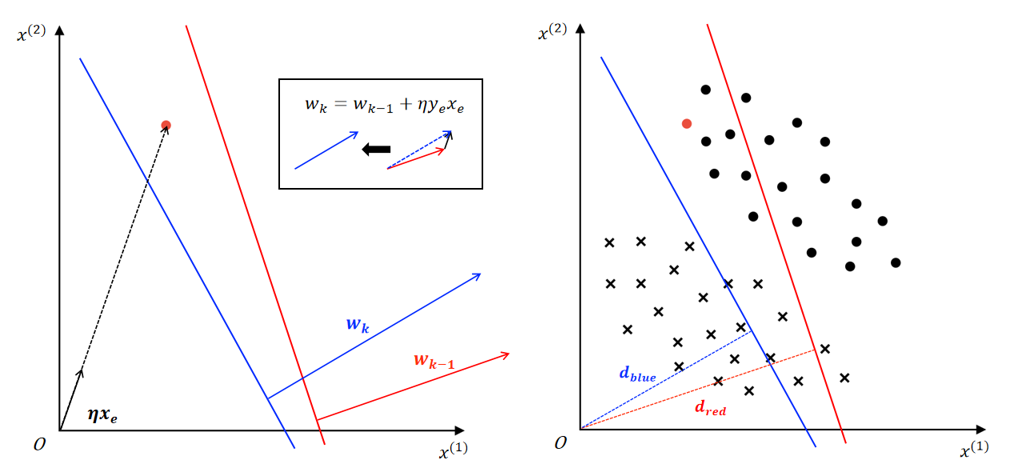
决策边界更新后，权向量由 \(w_{k-1} = (3,1)^T\) 调整为 \(w_k=(3.32,1.94)^T\)，表明更新后决策边界法向量方向朝 \(y_ex_e\) 向量的方向进行了一定程度的调整，参考如下左图；

决策边界更新后，偏置由 \(b_{k-1}=-12\) 调整为 \(b_k=-11.8\)；以 \((0,0)\) 为原点，分别代入红、蓝决策边界方程求决策边界到原点的距离： \(d_{red}=\dfrac{|b_{k-1}|}{||w_{k-1}||} \approx 3.79\;,\;d_{blue}=\dfrac{|b_k|}{||w_k||} \approx 3.07\)，表明更新后决策边界靠近了原点，参考如下右图。

---

示例 ③：

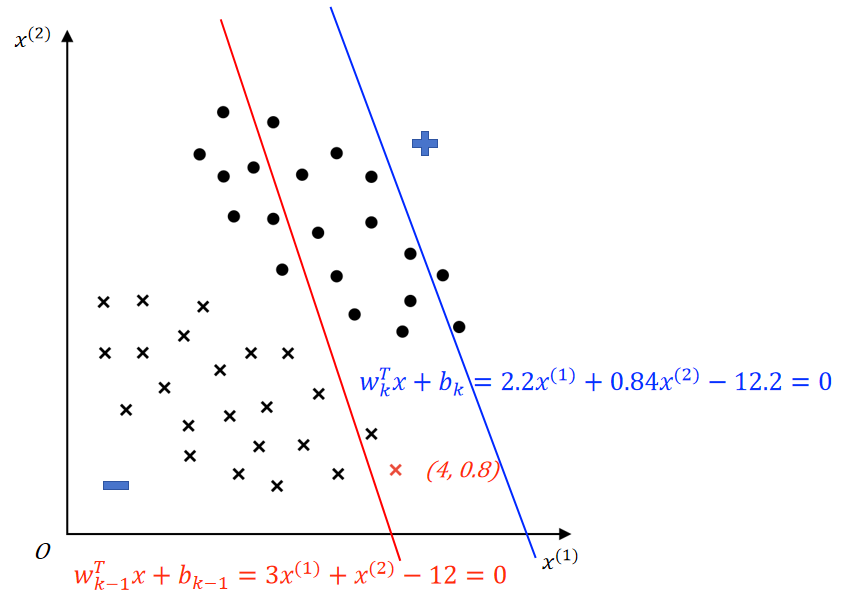
这里使用同示例 ②同特征空间分布，上图所示红色决策边界 \(w_{k-1}^Tx+b_{k-1}=3x^{(1)}+x^{(2)}-12=0\) 由第 \(k-1\) 次误分类更新所得，随机梯度下降过程中，选取了上图被红色决策边界误分类的红色负样本进行参数更新。（红色负样本 \(x_e=(4,0.8),y_e=-1\)，\(y_e(w_{k-1}^Tx_e+b_{k-1})=-1*(3*4+0.8-12)<0\)，即误分类）

参数更新（\(\eta=0.2\)）：

• 更新权向量 \(w\)
  • \(w_k = w_{k-1} + \eta y_ex_e=(3,1)^T + 0.2*(-1*(4,0.8)^T)=(2.2,0.84)^T\)
• 更新偏置 \(b\)
  • \(b_k = b_{k-1} + \eta y_e=-12 + 0.2*(-1)=-12.2\)

得到蓝色决策边界 \(w_k^Tx+b_k=2.2^{(1)}+0.84^{(2)}-12.2=0\)

可以发现：

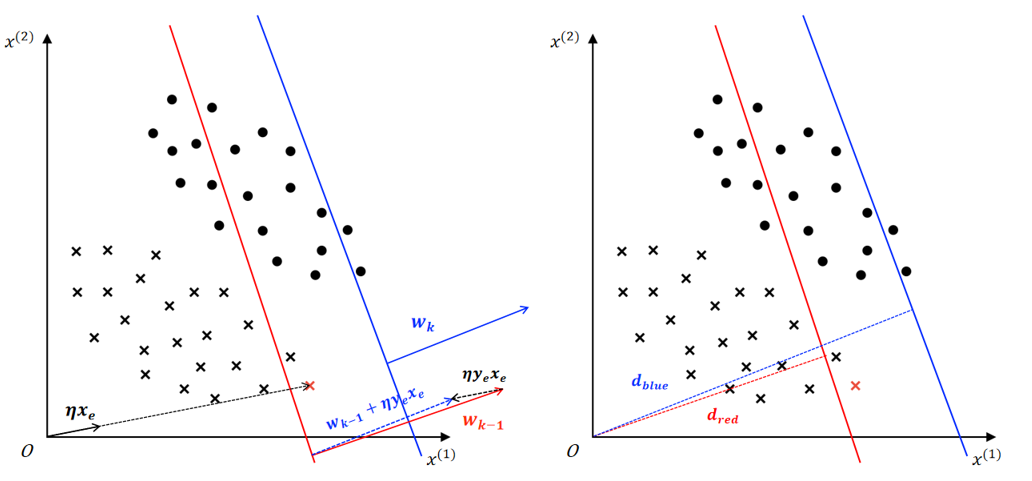
决策边界更新后，权向量由 \(w_{k-1} = (3,1)^T\) 调整为 \(w_k=(2.2,0.84)^T\)，表明更新后决策边界法向量方向朝 \(y_ex_e\) 向量的方向进行了一定程度的调整，参考如下左图；

决策边界更新后，偏置由 \(b_{k-1}=-12\) 调整为 \(b_k=-12.2\)；以 \((0,0)\) 为原点，分别代入红、蓝决策边界方程求决策边界到原点的距离： \(d_{red}=\dfrac{|b_{k-1}|}{||w_{k-1}||} \approx 3.79\;,\;d_{blue}=\dfrac{|b_k|}{||w_k||} \approx 5.18\)，表明更新后决策边界远离了原点，参考如下右图。

---

总结

① 感知机基于SGD更新参数时，利用选择的误分类样本向量及其类别，通过”向量相加“调整决策边界的方向，即法向量 \(w\) 的方向；利用选择的误分类样本的类别调整决策边界的位置

② 更新权向量（法向量）\(w\) 主要是在调整决策边界的方向，调整的幅度由步长（学习率）\(\eta\;\;(0<\eta\leq1)\) 决定。步长在SGD更新中起到调节梯度大小的作用，我们知道梯度是函数值变化最快的方向，在感知机的SGD更新中梯度表现为向量 \(y_ix_i\)，若直接使用原梯度调整 \(w\) 可能出现调整幅度过大导致跳过最优解的现象，所以需要利用步长 \(\eta\) 调整梯度大小，限制调整的幅度。如下图右图所示，对示例 ①的红色决策边界使用不同 \(\eta\) 进行参数更新得到不同的结果，可见较大的 \(\eta\) （对应较大的梯度）得到的决策边界不利于模型的收敛，而较小的 \(\eta\) 虽然降低了调整幅度，但整体上是有利于模型收敛的。

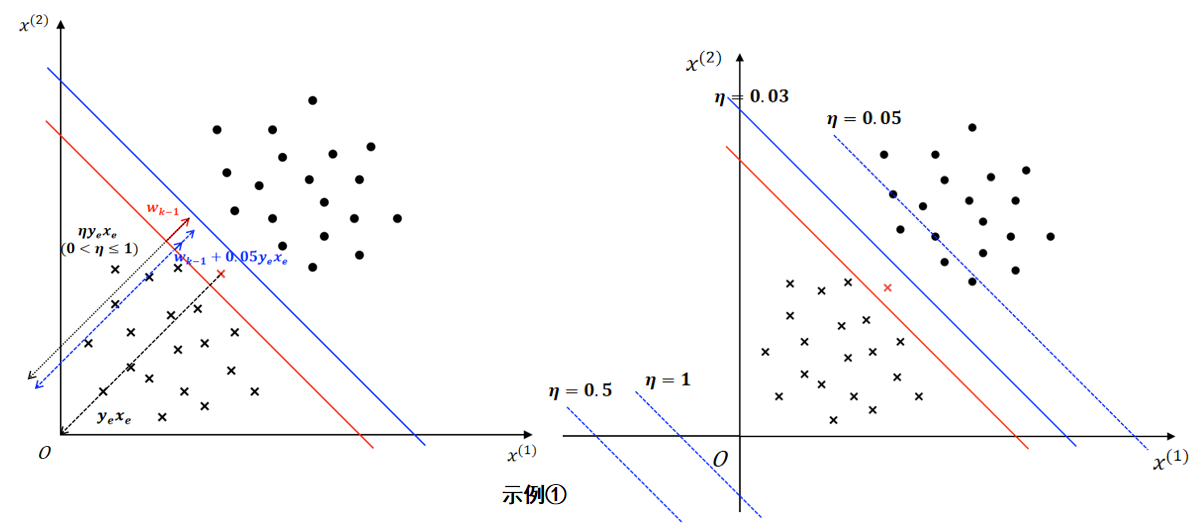
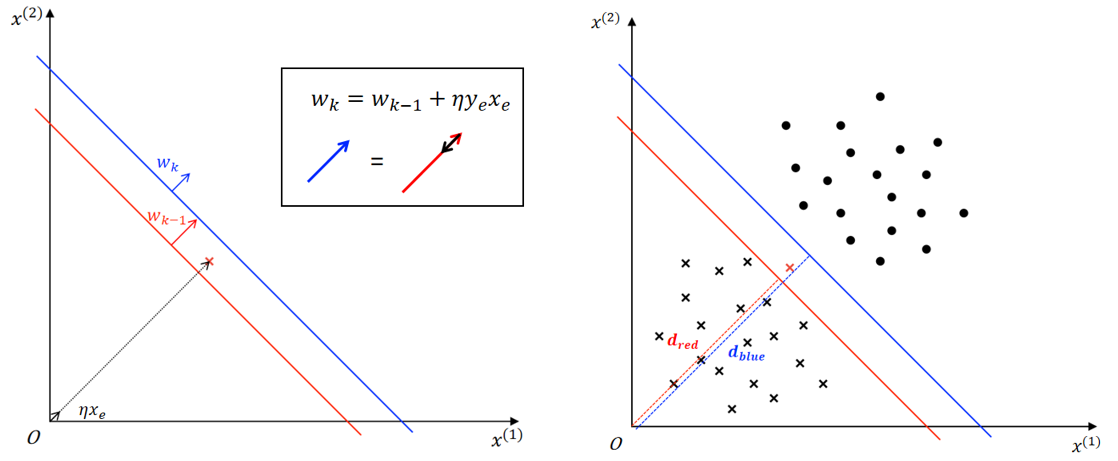
③ 当感知机SGD更新过程中，若选取的样本向量和当前决策边界法向量方向在同一直线上（同向或反向），那么更新得到决策边界”角度“方向不变（意思是得到的 \(w_k\) 和 \(w_{k-1}\) 在同一直线上），决策边界的更新实际上在平移，如上图所示的示例 ①。否则 \(w_k = w_{k-1} + \eta y_ex_e\) 将改变法向量的方向，且不同的 \(\eta\) 得到的法向量方向不同。下图给出示例②③中 \(w\) 和 \(\eta y_ex_e\) 的关系。

④ 感知机SGD对偏置 \(b\) 的更新是基于选取的误分类样本类别的，\(b_k = b_{k-1} + \eta y_e\) 可以理解为通过改变偏置的大小进而改变函数间隔 \(y_e(w^Tx_e+b)\) 的大小。函数间隔的正负和大小具有分类准确性和置信度的意义，对于误分类的样本，若正样本 \((x_e,y_e)\) 被误分类，那么 \(y_e(w^Tx_e+b)\leq0\) 且 \(w^Tx_e+b\leq0\)，于是 \(b_k = b_{k-1} + \eta y_e > b_{k-1}\)，旨在增大 \(w^Tx_e+b(\leq0)\) 的值，相当于削弱了将正样本 \((x_e,y_e)\) 划分为负类的置信度。反之对于负样本同理，\(b_k = b_{k-1} + \eta y_e < b_{k-1}\)，旨在增大 \(w^Tx_e+b(\geq0)\) 的值，相当于削弱了将负样本划分为正类的置信度。

⑤ 感知机SGD过程中每次更新的决策边界的位置（距离原点的距离）实际上是由 \(w\) 和 \(b\) 共同决定的（\(d=\dfrac{|b|}{||w||}\))，因为 \(w\) 和 \(b\) 改变的程度通常是不对等的。

1.6.2 损失函数为什么不用几何间隔

测量误分类样本到决策边界的几何距离（欧式距离）可以通过 \(\dfrac{|w^Tx_i + b|}{||w||}\) 实现，而要进一步表现分类效果，可以使用几何间隔的表式：\(\dfrac{-y_i(w^Tx_i + b)}{||w||}\)

对于误分类样本集 \(M\) 某个被误分类的样本 \((x_i,y_i)\)：

• 判别函数满足：\(y_i(w^Tx_i+b)\leq0\)
• 点到超平面距离：\(\dfrac{|w^Tx_i + b|}{||w||}\)，误分类点到超平面距离可表示为：\(\dfrac{-y_i(w^Tx_i + b)}{||w||}\)
  • \(||w||\) 是 \(w\) 的 \(L2\) 范数，即 \(w\) 的模：\(||w|| = \sqrt{w_1^2+w_2^2+\dots+w_d^2} = \sqrt{w^Tw}\)

误分类点到超平面总距离：\(L(w,b) = \sum_{x_i \in M}{\dfrac{-y_i(w^Tx_i + b)}{||w||}}\)

损失函数同样是基于误分类点所表示的，当存在误分类样本时，\(L(w,b)\) 是 \(w,b,(w\neq0)\) 的连续可导函数；当不存在误分类样本时（\(M=\emptyset\)），损失函数应为 0

根据感知机的学习策略，有优化目标：\(\min_{w,b}{L(w,b)} = \min_{w,b}{\sum_{x_i \in M}{\dfrac{-y_i(w^Tx_i + b)}{||w||}}}\)

感知机可采用梯度下降算法（SGD）对目标函数进行优化，每次（随机）选取一个误分类样本对应的损失计算梯度，利用梯度更新 \(w,b\)

损失函数引入范数约束后进行SGD：

• \(\nabla_wL(w,b) = \dfrac{(-y_ix_i)||w|| - (-y_i(w^Tx_i+b))\frac{w}{||w||}}{||w||^2} = \dfrac{-y_ix_i}{||w||}+\dfrac{y_i(w^Tx_i+b)w}{||w||^3}\)

• \(\nabla_bL(w,b) = \dfrac{-y_i}{||w||}\)

• 随机选取一个误分类点 \((x_i,y_i)\) 更新 \(w,b\)：

  • \(w^+ \longleftarrow w - \eta\nabla_wL(w,b) = w + \eta\dfrac{1}{||w||}y_ix_i-\dfrac{y_i(w^Tx_i+b)}{||w||^3}w\)
  • \(b^+ \longleftarrow b - \eta\nabla_bL(w,b) = b + \eta\dfrac{y_i}{||w||}\)

• 对比使用函数间隔的SGD参数更新：

  • \(w^+ \longleftarrow w - \eta\nabla_wL(w,b) = w + \eta y_ix_i\)

  • \(b^+ \longleftarrow b - \eta\nabla_bL(w,b) = b + \eta y_i\)

  • 简化前后 \(w\) 更新的梯度方向都是是由误分类点 \(y_ix_i\) 决定，原更新中使用 \(\dfrac{1}{||w||}\) 对 \(w,b\) 更新的学习率进行了调整

  • 原损失函数 \(w\) 的更新额外包含了对 \(w\) 的大小调整

  • 所以简化前后 \(w,b\) 的更新方向是一样的，因此两者的优化

可以发现，原损失函数引入范数后，计算梯度和参数更新涉及的计算变得复杂，感知机学习的最终目标是希望没有误分类的样本，此时损失函数值应为 0，即 \(M = \emptyset\)。注意这里的最小值 0 是因为误分类集合 \(M\) 为空集而获取的，这表明感知机的学习策略关注的是 \(M\) 中样本的数量。当每次SGD更新参数时，决策超平面都会改善在一个误分类样本点上的表现，这是一种局部的改善，可能导致误分类样本临时的增加或减少，但总体上决策超平面在不断地接近某个能正确划分所有样本的情况。

函数间隔和几何间隔都可以表示分类的正确性和置信度。函数间隔存在“参数等比例变化，超平面不变，函数间隔改变”的问题，几何间隔对函数间隔加以范数约束，避免了这个问题，这使得测量得到的距离之间更具有可比性。但感知机不在意这个距离到底是多少，只关心误分类样本的数量，且算法只有在满足条件后才会终止，所以参数等比例变化的情况最终会被淘汰。

综上，感知机使用更简洁的函数间隔作为损失函数，且已被证明收敛性。

参考

[1] 李航. 机器学习方法. 北京: 清华大学出版社, 2012.

[2] Wang, Q., Ma, Y., Zhao, K. et al. A Comprehensive Survey of Loss Functions in Machine Learning. Ann. Data. Sci. 9, 187–212 (2022). https://doi.org/10.1007/s40745-020-00253-5

[3] Block, H.D. (1962). The perceptron: a model for brain functioning. I.

[4] CS440 Lectures (illinois.edu)

SVM支持向量机