单变量微积分学习笔记：三角函数常用公式（8）

和差角公式

公式

\(\sin(a \pm b) = \sin(a)\cos(b) \pm \cos(a)\sin(b)\)
\(\cos(a \pm b) = \cos(a)\cos(b) \mp \sin(a)\sin(b)\)
\(\tan(a \pm b) = \sin(a)\cos(b) \pm \cos(a)\sin(b)\)

证明（补）

\(\tan(a \pm b) = \frac{\sin(a \pm b)}{\cos(a \pm b)} = \frac{\sin(a)\cos(b) \pm \cos(a)\sin(b)}{\cos(a)\cos(b) \mp \sin(a)\sin(b)} = \frac{\tan(a) \pm \tan(b)}{1 \mp \tan(a)\tan(b)}\)

---

诱导公式（奇变偶不变，符号看象限）

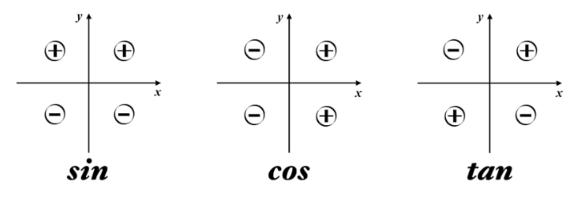
\[\begin{matrix} sin \\ cos \\ tan \end{matrix}\ (n\frac{\pi}{2}\pm\beta) = \ \ (象限) \ \ \left\{\begin{matrix} +\\ - \end{matrix}\right. \ \ (奇偶) \ \ \begin{matrix} \left\{\begin{matrix} \begin{matrix} sin \\ cos \\ tan \end{matrix} ,n\mod2=0\\\\ \begin{matrix} cos \\ sin \\ cot \end{matrix},n\mod2=1 \end{matrix}\right.\\ \end{matrix}\ \ \ \ \ \ \ \ (\beta) \]