POJ 2507 Crossed ladders

题目链接：POJ 2507 Crossed ladders

题目大意：

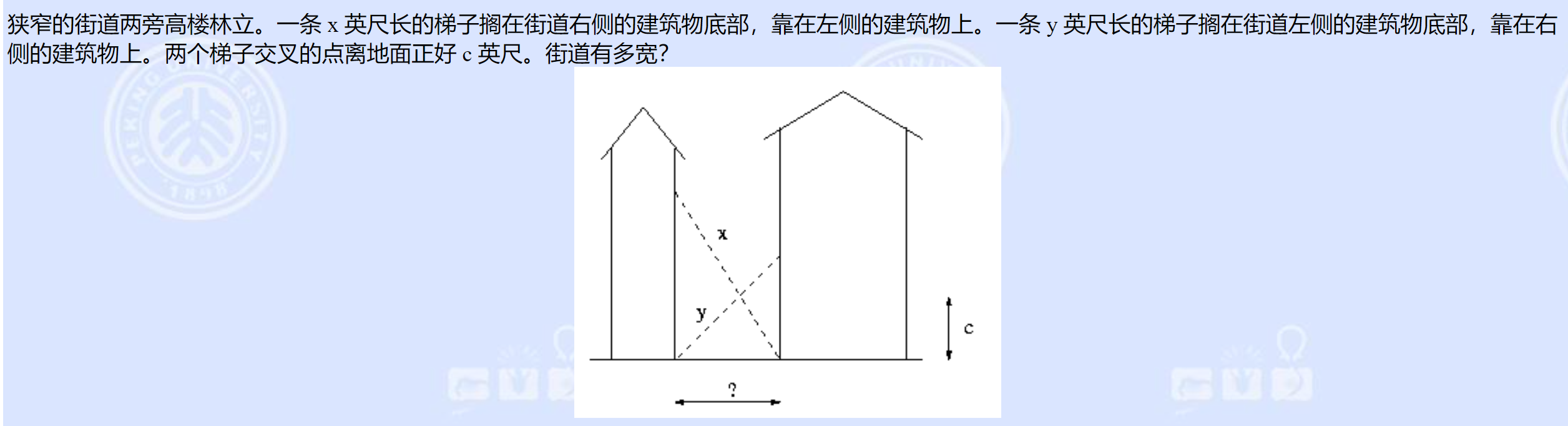
题解：

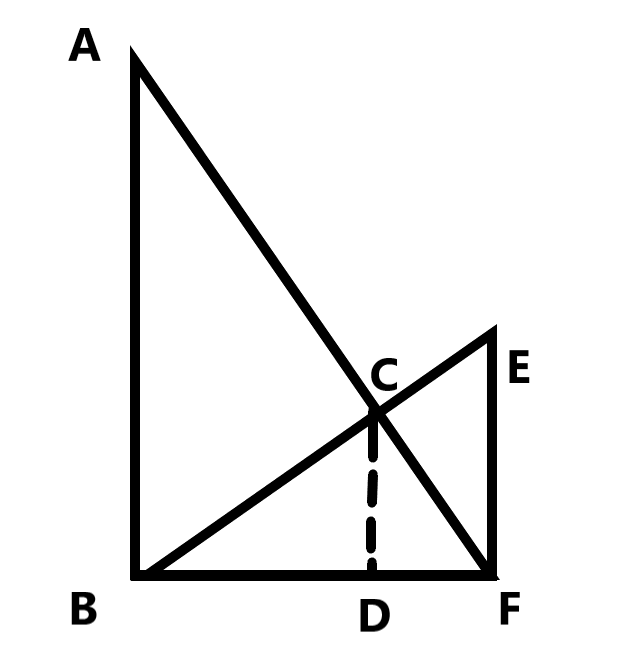
如图所示，已知\(\left\{\begin{aligned}\frac{CD}{AB}=\frac{DF}{BF}\\\frac{CD}{EF}=\frac{BD}{BF}\end{aligned}\right.\)，
两式相加得\(\frac{CD}{AB}+\frac{CD}{EF} = 1\)，
等式两边同时乘以\(AB\times EF\)得\(CD\times (AB + EF) = AB\times EF\)，
代入题目中，设两楼之间距离为\(d\)，则可得\(c \times (\sqrt{x^2 - d^2} + \sqrt{y^2 - d^2}) = \sqrt{x^2 - d^2} \times \sqrt{y^2 - d^2}\)。
对\(d\)进行二分答案，由于是浮点数所以需要设置二分的次数限制。

#include <cmath>
#include <iomanip>
#include <iostream>
using namespace std;

double x, y, c;

bool judge(double d) {
    double t1 = sqrt(x * x - d * d);
    double t2 = sqrt(y * y - d * d);
    if (t1 * t2 >= c * (t1 + t2)) {
        return true;
    } else {
        return false;
    }
}

int main() {
    while (cin >> x >> y >> c) {
        double l = 0, r = min(x, y), mid;
        int cnt = 99;
        while (cnt--) {
            mid = (l + r) / 2.0;
            if (judge(mid)) {
                l = mid;
            } else {
                r = mid;
            }
        }
        cout << fixed << setprecision(3) << mid << endl;
    }
    return 0;
}