CF1715F题解

CF1715F

这里更容易进入且有翻译

题意

给定一个 $n\times m$ 的矩形区域，区域内有一个边长为 $1$ 的正方形。交互最多五次进行询问，每次询问可以给出一个不自交的多边形（不要求为凸多边形），评测姬返回该多边形与正方形的交的面积。要求猜测正方形的靠原点方向的顶点坐标 $(x,y)$。

解析

这题在CF上有计算几何标签，但没涉及什么计算几何相关，更像是一道思维题。

官方题解为使用横纵两个方向的锯齿形多边形进行两次询问。这里使用另一种思路，仅从横向（或纵向）单个方向构造多边形，使用 2 到 3 次询问。

这里使用下面样例进行解释：

6 5
2.2 3

由于要查找的正方形边长固定为 $1$，我们以上面样例构造如下图的矩形波：

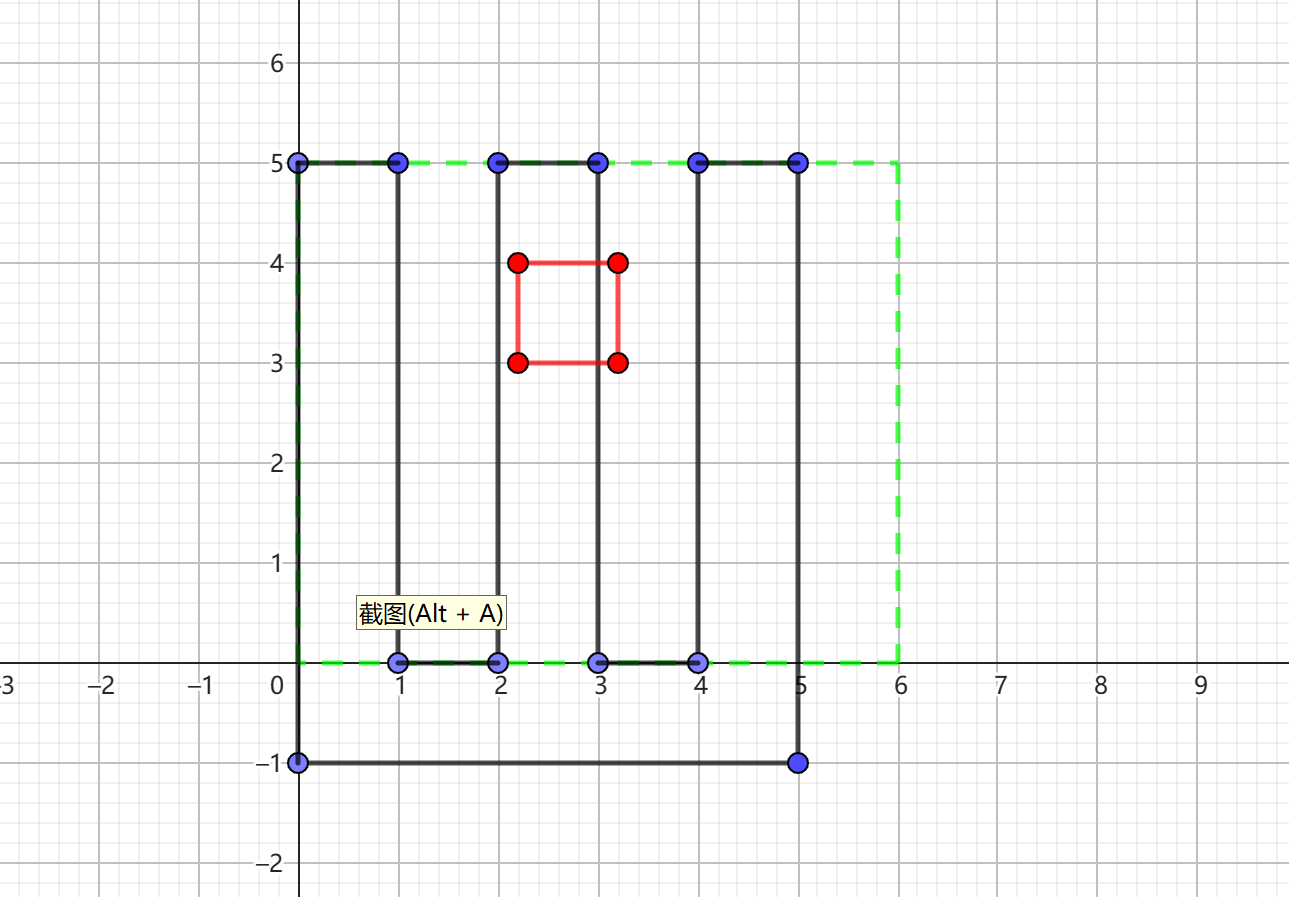
作为第一次询问，我们得到 $re{s}_1$，得到的结果用于后面对齐询问的横坐标，此时的询问能计算出 $x$ 为 $C+re{s}_1$ 或 $C-re{s}_1$，其中 $C$ 为整数。

第二次询问将第一次询问的多边形向右移动 $1-re{s}_1$，确认 $x$ 为 $C+re{s}_1$ 还是 $C-re{s}_1$。如下图：

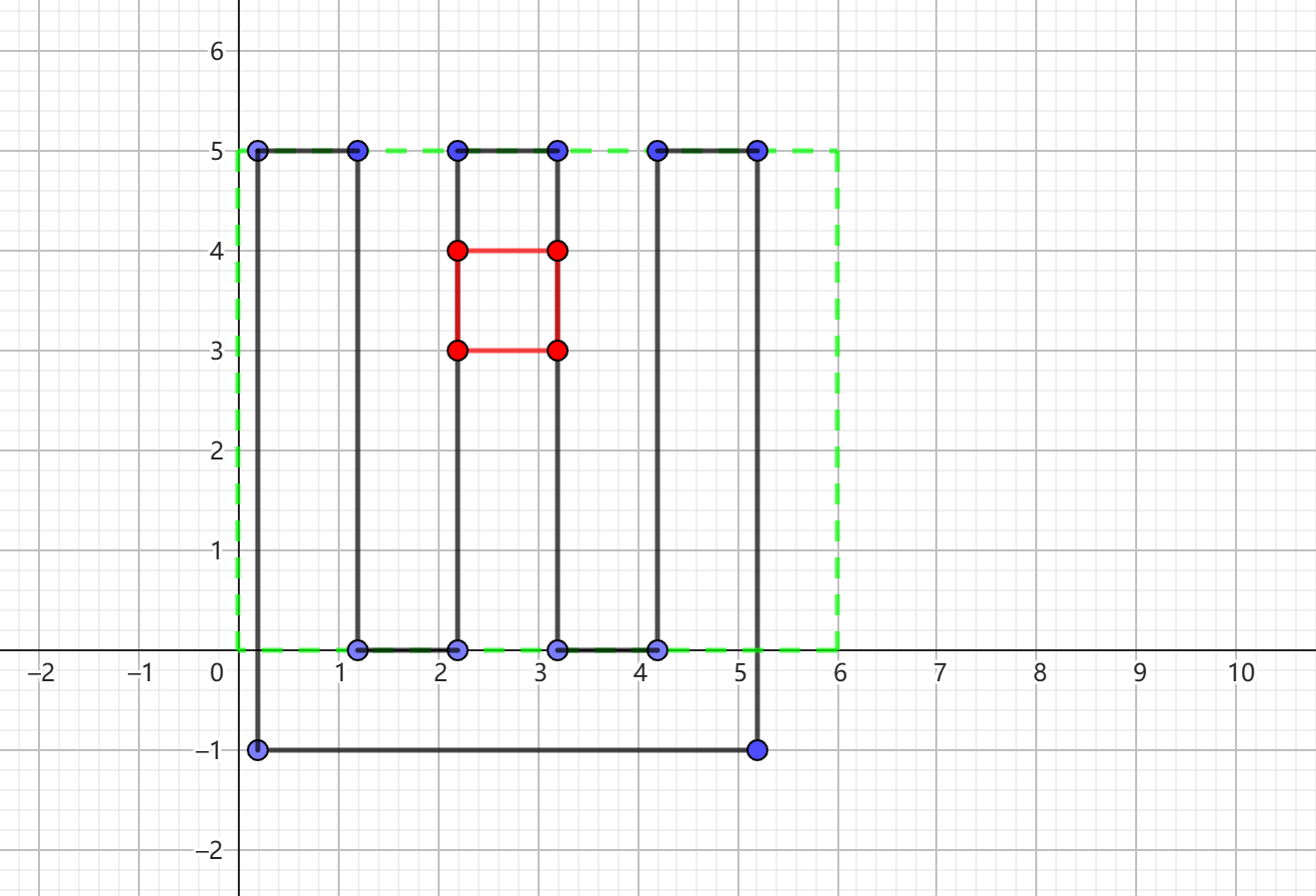
如果询问得到的 $re{s}_2$ 为 $1$ 则 $x$ 为 $C-re{s}_1$。

第三次询问。先设偏移距离 $l$，若 $x=C-re{s}_1$ 则 $l=1-re{s}_1$；否则 $l=re{s}_1$。

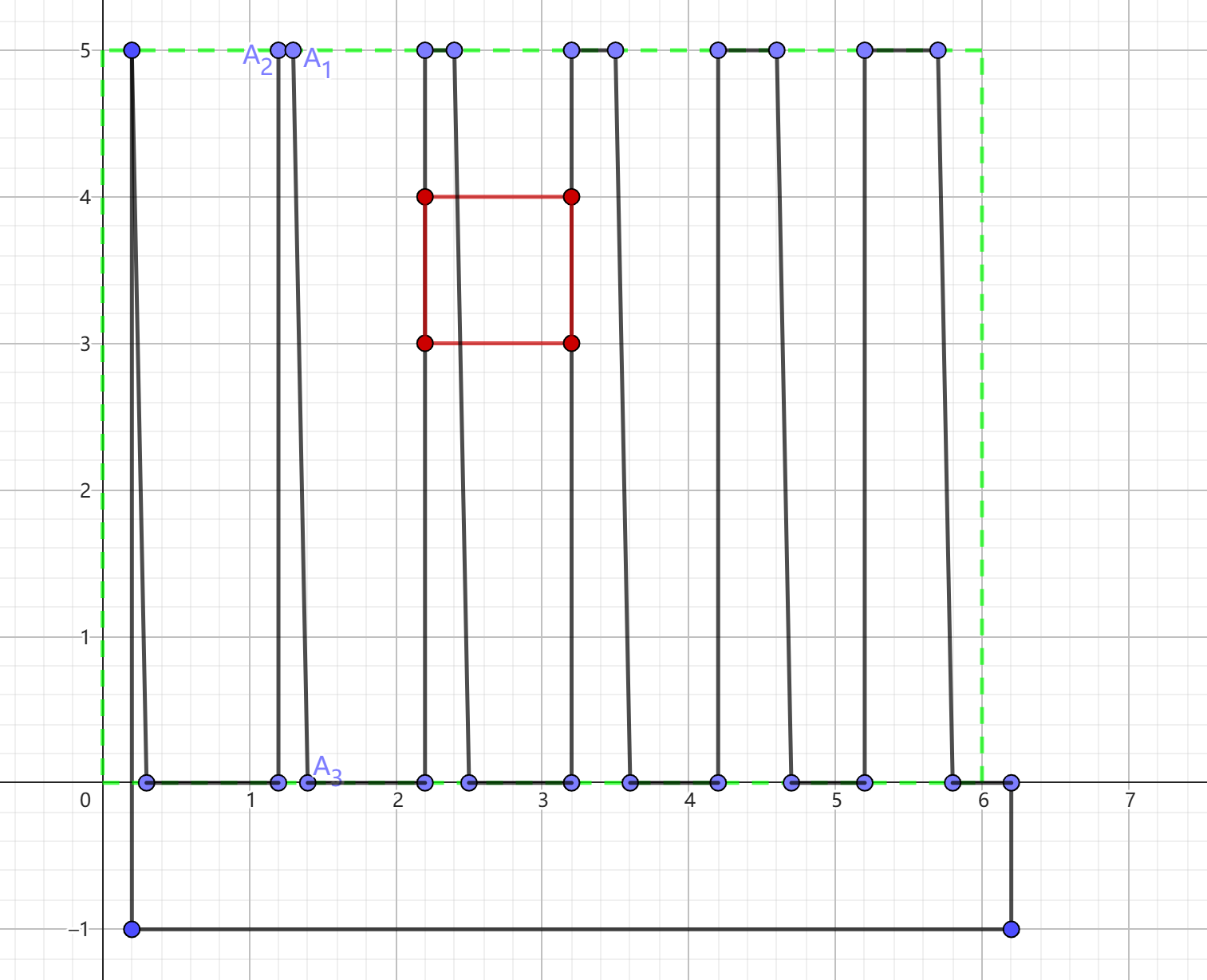
构造如图多边形，如图中所示，$A_1{A}_2$ 及其它与 $A_1{A}_2$ 位于同一直线上的线段的长度成等差数列，设 $step$，这些线段的长度从左到右依次为 $step,step\times 2,step\times 3,\dots ,step\times (n-1)$；$A_1{A}_3$ 及其它斜线斜率 $k$ 均为 $-\frac{m}{step}$。

第三次询问得到的面积 $re{s}_3$，则有答案：

$$x=l+\lfloor \frac{re{s}_3}{step}\rfloor$$

$$y=k\times (re{s}_3-\lfloor \frac{re{s}_3}{step}\rfloor \times step)+m-0.5$$

（利用直线方程 $y_0=k\times x_0+m$ 计算得到的结果为正方形中心的纵坐标，因而需要减去 $0.5$）。

代码

#include <bits/stdc++.h>
#include <unordered_map>
#define LL long long
#define pii pair<int, int>
#define pll pair<LL, LL>
#define double long double
#define pdd pair<double, double>
#define eps 1e-15

using namespace std;

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    int n, m;
    double res1, res2, l, res3;
    cin >> n >> m;
    
    //第一次询问
    printf("? %d\n", max(n + 1 >> 1 << 2, 8)); //这里取至少8是因为循环前后直接进行了两次坐标输出
    printf("0 -1\n0 %d\n1 %d\n1 0\n", m, m);
    int idx = 3;
    for (; idx <= n - 2; idx += 2)
        printf("%d 0\n%d %d\n%d %d\n%d 0\n", idx - 1, idx - 1, m, idx, m, idx);
    printf("%d 0\n%d %d\n%d %d\n%d -1\n", idx - 1, idx - 1, m, idx, m, idx);
    fflush(stdout);
    cin >> res1;

    if (fabs(res1 - (double)1.0) <= eps || fabs(res1 - (double)0.0) <= eps) //对横坐标在允许误差内是否为整数进行判断
        l = 0.0;
    else
    {
        //第二次询问
        printf("? %d\n",max(n + 1 >> 1 << 2, 8));
        printf("%.15LF -1\n%.15LF %d\n%.15LF %d\n%.15LF 0\n", (double)1.0 - res1, (double)1.0 - res1, m, (double)2.0 - res1, m, (double)2.0 - res1);
        int idx = 3;
        for (; idx <= n - 2; idx += 2)
            printf("%.15LF 0\n%.15LF %d\n%.15LF %d\n%.15LF 0\n", (double)idx - res1, (double)idx - res1, m, (double)(idx + 1) - res1, m, (double)(idx + 1) - res1);
        printf("%.15LF 0\n%.15LF %d\n%.15LF %d\n%.15LF -1\n", (double)idx - res1, (double)idx - res1, m, (double)(idx + 1) - res1, m, (double)(idx + 1) - res1);
        fflush(stdout);
        cin >> res2;

        if (fabs(res2 - (double)1.0) <= eps)
            l = (double)1.0 - res1;
        else
            l = res1;
    }

    //第三次询问
    printf("? %d\n", (n << 2) + 1);
    double step = 0.00390625; //步长设为2的幂次防止丢精度
    printf("%.15LF -1\n%.15LF -1\n%.15LF %d\n%.15LF 0\n%.15LF 0\n", l + (double)n, l, l, m, l + step, l + (double)1.0);
    for (int i = 1; i < n; i++)
        printf("%.15LF %d\n%.15LF %d\n%.15LF 0\n%.15LF 0\n", l + (double)i, m, l + (double)i + (double)i * step, m, l + (double)i + (double)(i + 1) * step, l + (double)(i + 1));
    fflush(stdout);
    cin >> res3;

    int xi = res3 / step;
    double x = (double)xi + l, y = (double)m - (res3 - (double)xi * step) * ((double)m / step) - (double)0.5;

    printf("! %.15LF %.15LF\n", x, y);
    fflush(stdout);
}

最后祝各位顺利AC。>w<