电磁辐射相关物理量

辐射能量 \(Q\)

平平无奇的能量，就是能量，纯能量，辐射出来的能量……

先引入时间——辐射通量 \(\Phi\)

\[\Phi = \frac{dQ}{dt} \]

因为辐射通量是能量对时间求导，所以我更愿意结合其他物理量理解，故称其为辐射功率（也确实可以这么叫）

高中时候学的磁通量是\(\Phi = BS\cos\theta\)，在这里容易搞混，有亿点SB

再引入面积——辐照度 & 辐射出射度 \(E\ \And \ M\) (辐射通量密度)

\[E\ \And \ M = \frac{d\Phi}{dS} \]

或引入立体角(方位) \(\Omega\) ——辐射强度 \(I\)

等等，立体角是什么？

平面角是单位圆上的一段弧长，所以立体角是单位球面上的一块面积

在球坐标系中，半径为 \(r\) 的球面的极小面积为：

\[dA = (r\sin\theta\ d\varphi)(r\ d\theta)=r^2(\sin\theta\ d\theta\ d\varphi) \]

因此极小立体角，即单位球面上的极小面积为：

\[d\Omega = \frac{dA}{r^2} = \sin\theta\ d\theta\ d\varphi \]

所以最终

\[d\Omega = \sin\theta\ d\theta\ d\varphi \]

单位为球面度(sr)

所以，给辐射通量 \(\Phi\) 引入立体角 \(\Omega\) ——辐射强度 \(I\)

\[I = \frac{d\Phi}{d\Omega} \]

PS：我在试图理解这个概念的过程中，在立体角这里付出了尤其多的时间，因为我的数学能力十分薄弱，导致把立体角当做了一小块球面的面积来理解，以至于和S发生了混淆（我以为区别在于一个是球面，一个是平面，我是傻逼）。然而实际上，立体角本质上代表的是方向，方向，方向！与其说是引入了立体角，其实就是引入了观测方向，最简单的例子就是你在不同的方向观察一个物体，物体的成像形状是不同的。我是傻逼。

最终，我们同时引入面积 \(S\) 和立体角 \(\Omega\) ——辐射亮度 \(L\)

\[L = \frac{d^2\Phi}{dA\ d\Omega} \]

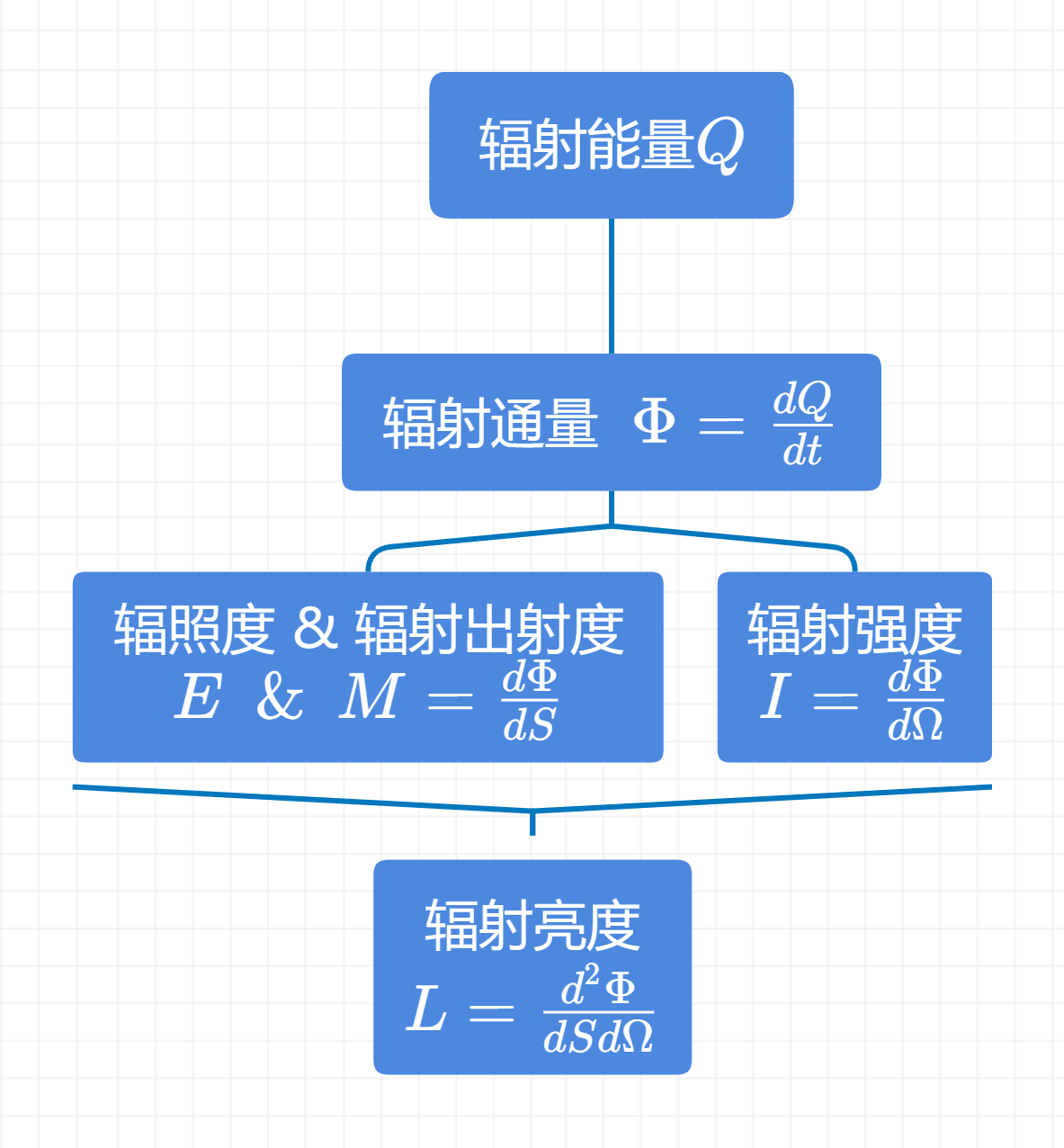
总结

就是：