P5016 [NOIP2018 普及组] 龙虎斗

P5016 [NOIP2018 普及组] 龙虎斗

题目

轩轩和凯凯正在玩一款叫《龙虎斗》的游戏，游戏的棋盘是一条线段，线段上有 \(n\) 个兵营（自左至右编号 \(1 \sim n\)），相邻编号的兵营之间相隔 \(1\) 厘米，即棋盘为长度为 \(n-1\) 厘米的线段。\(i\) 号兵营里有 \(c_i\)位工兵。 下面图 1 为 \(n=6\) 的示例：

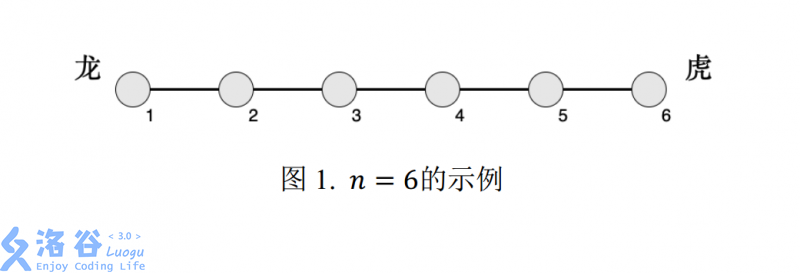
轩轩在左侧，代表“龙”；凯凯在右侧，代表“虎”。 他们以 \(m\) 号兵营作为分界， 靠左的工兵属于龙势力，靠右的工兵属于虎势力，而第 \(m\) 号兵营中的工兵很纠结，他们不属于任何一方。

一个兵营的气势为：该兵营中的工兵数$ \times $ 该兵营到 \(m\) 号兵营的距离；参与游戏 一方的势力定义为：属于这一方所有兵营的气势之和。
下面图 2 为 \(n = 6,m = 4\) 的示例，其中红色为龙方，黄色为虎方：

游戏过程中，某一刻天降神兵，共有 \(s_1\) 位工兵突然出现在了 \(p_1\) 号兵营。作为轩轩和凯凯的朋友，你知道如果龙虎双方气势差距太悬殊，轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续，你需要选择一个兵营 \(p_2\)，并将你手里的 \(s_2\) 位工兵全部派往 兵营 \(p_2\)，使得双方气势差距尽可能小。

注意：你手中的工兵落在哪个兵营，就和该兵营中其他工兵有相同的势力归属（如果落在 \(m\) 号兵营，则不属于任何势力）。

输入

输入文件的第一行包含一个正整数\(n\)，代表兵营的数量。

接下来的一行包含 \(n\) 个正整数，相邻两数之间以一个空格分隔，第 \(i\) 个正整数代 表编号为 \(i\) 的兵营中起始时的工兵数量 \(c_i\)。

接下来的一行包含四个正整数，相邻两数间以一个空格分隔，分别代表 \(m,p_1,s_1,s_2\)。

输出

输出文件有一行，包含一个正整数，即 \(p_2\)，表示你选择的兵营编号。如果存在多个编号同时满足最优，取最小的编号。

样例 1

输入

6 
2 3 2 3 2 3 
4 6 5 2

输出

2

样例 2

输入

6 
1 1 1 1 1 16 
5 4 1 1

输出

1

提示

样例 1 说明
见问题描述中的图 2。
双方以 \(m=4\) 号兵营分界，有 \(s_1=5\) 位工兵突然出现在 \(p_1=6\) 号兵营。
龙方的气势为：

\[2 \times (4-1)+3 \times (4-2)+2 \times (4-3) = 14 \]

虎方的气势为：

\[2 \times (5 - 4) + (3 + 5) \times (6 - 4) = 18 \]

当你将手中的 \(s_2 = 2\) 位工兵派往 \(p_2 = 2\) 号兵营时，龙方的气势变为：

\[14 + 2 \times (4 - 2) = 18 \]

此时双方气势相等。

样例 2 说明
双方以 \(m = 5\) 号兵营分界，有 \(s_1 = 1\) 位工兵突然出现在 \(p_1 = 4\) 号兵营。
龙方的气势为：

\[1 \times (5 - 1) + 1 \times (5 - 2) + 1 \times (5 - 3) + (1 + 1) \times (5 - 4) = 11 \]

虎方的气势为：

\[16 \times (6 - 5) = 16 \]

当你将手中的 \(s_2 = 1\) 位工兵派往 \(p_2 = 1\) 号兵营时，龙方的气势变为：

\[11 + 1 \times (5 - 1) = 15 \]

此时可以使双方气势的差距最小。

数据规模与约定
\(1 < m < n,1 ≤ p_1 ≤ n\)。
对于 \(20\%\) 的数据，\(n = 3,m = 2, c_i = 1, s_1,s_2 ≤ 100\)。
另有 \(20\%\) 的数据，\(n ≤ 10, p_1 = m, c_i = 1, s_1,s_2 ≤ 100\)。
对于 \(60\%\) 的数据，\(n ≤ 100, c_i = 1, s_1,s_2 ≤ 100\)。
对于 \(80\%\) 的数据，\(n ≤ 100, c_i,s_1,s_2 ≤ 100\)。
对于 \(100\%\) 的数据，\(n≤10^5\),\(c_i,s_1,s_2≤10^9\)。

---

思路

以 \(m\) 为界限，龙的势力和虎的势力也可以计算出来，顺便将天降神兵的势力也累加到龙或虎的势力中。选择一个兵营 \(p_2\)，并将手里的 \(s_2\) 位工兵全部派往兵营 \(p_2\)，一旦我们知道 \(p_2\) 具体是哪个兵营的，就可以累加到对应的龙或者虎的势力中（判断 \(p_2\) 和 \(m\) 的关系）。容易得到，\(p_2\) 的范围是 \(1\) 到 \(n\)。因此通过分析题目，提取恰当状态进行枚举，即枚举 \(p_2\)，可以得到两方势力之差。神兵可以降到 \(m\) 的位置，那么此时两方的势力已经求出，可以将该势力差作为擂主，通过打擂台的方式，得知使得两方势力差距最小的位置。

值得注意的一点是，\(100 \%\) 数据中势力的大小不超过 \(10^9\)，累加后超过 \(\operatorname{int}\) 范围，因此代码中需要使用 \(\operatorname{long long}\) 类型保存势力大小的数值。

---

代码

#include <bits/stdc++.h>

using namespace std;

long long n, c[100005], m, p1, s1, s2, p, sum1, sum2, mn, ans1, ans2;

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++ )
		cin >> c[i];
	cin >> m >> p1 >> s1 >> s2;
	c[p1] += s1; // 有 s1 位工兵降落到 p1 位置
	for (int i = 1; i < m; i ++ )
		sum1 = sum1 + c[i] * (m - i);
	for (int i = m + 1; i <= n; i ++ )
		sum2 = sum2 + c[i] * (i - m);
	// 后面要枚举 s2 个士兵放置位置，可将 s2 个工兵放在 m 位置，则两方之差为
	mn = abs(sum1 - sum2);
	p = m; // mn 作为数值的擂主，不要忘了 p
	for (int j = 1; j <= n; j ++ )
	{
		ans1 = sum1;
		ans2 = sum2;
		// 注意要拷贝到新的变量，不要改变原来的势力值
		if (j < m)
			ans1 += (m - j) * s2;
		else if (j > m)
			ans2 += (j - m) * s2;
		if (abs(ans1 - ans2) < mn)
		{
			mn = abs(ans1 - ans2);
			p = j;
		}
	}
	cout << p << '\n';
	return 0;
}