ACM/ICPC 之 数论-斐波拉契●卢卡斯数列(HNNUOJ 11589)
看到这个标题,貌似很高大上的样子= =,其实这个也是大家熟悉的东西,先给大家科普一下斐波拉契数列。
- 斐波拉契数列
又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……
在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)
在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
- 斐波拉契数列与黄金分割-----(涉及今天的例题)
有趣的是:这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618.(或者说后一项与前一项的比值小数部分越来越逼近黄金分割0.618、前一项与后一项的比值越来越逼近黄金分割0.618)
1÷1=1,1÷2=0.5,2÷3=0.666...,3÷5=0.6,5÷8=0.625,…………,55÷89=0.617977…,…………144÷233=0.618025…46368÷75025=0.6180339886…...
越到后面,这些比值越接近黄金比.
- 斐波拉契数列-部分数学规律
偶数项求和![]()
平方求和![]()
以下正式入题啦~
- 斐波拉契-卢卡斯数列
卢卡斯数列1、3、4、7、11、18…,也具有斐波那契数列同样的性质。(我们可称之为斐波那契—卢卡斯递推:从第三项开始,每一项都等于前两项之和f(n) = f(n-1)+ f(n-2)。
这两个数列还有一种特殊的联系(如下表所示),F(n)*L(n)=F(2n),及L(n)=F(n-1)+F(n+1)
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
…
|
|
斐波那契数列F(n)
|
1
|
1
|
2
|
3
|
5
|
8
|
13
|
21
|
34
|
55
|
…
|
|
卢卡斯数列L(n)
|
1
|
3
|
4
|
7
|
11
|
18
|
29
|
47
|
76
|
123
|
…
|
|
F(n)*L(n)
|
1
|
3
|
8
|
21
|
55
|
144
|
377
|
987
|
2584
|
6765
|
…
|
类似的数列还有无限多个,我们称之为斐波那契—卢卡斯数列。
如1,4,5,9,14,23…,因为1,4开头,可记作F[1,4],斐波那契数列就是F[1,1],卢卡斯数列就是F[1,3],斐波那契—卢卡斯数列就是F[a,b]。
- 与斐波拉契数列的另一个共同性质:
- 中间项的平方数与前后两项之积的差的绝对值是一个恒值
斐波那契数列:|1*1-1*2|=|2*2-1*3|=|3*3-2*5|=|5*5-3*8|=|8*8-5*13|=…=1
卢卡斯数列:|3*3-1*4|=|4*4-3*7|=…=5
F[1,4]数列:|4*4-1*5|=11
F[2,5]数列:|5*5-2*7|=11
F[2,7]数列:|7*7-2*9|=31
- 黄金特征-----(与例题有关)
斐波那契数列这个值是1最小,也就是前后项之比接近黄金比例最快,我们称为黄金特征
黄金特征1的数列只有斐波那契数列,是独生数列。卢卡斯数列的黄金特征是5,也是独生数列。
前两项互质的独生数列只有斐波那契数列和卢卡斯数列这两个数列。
应用例题:

题意:大致就是给定一个斐波拉契-卢卡斯数列中的某一项an(题目没有说明,但是这其实就是斐波拉契卢卡斯数列),然后让你求出初始的斐波拉契-卢卡斯数列a1和a2的值,并使得a2尽可能小。
我用的是数学规律的思路
- 在一个斐波拉契-卢卡斯数列的无穷大项(记为第m项),则第m-1项除以m项一定无限接近黄金分割0.618---可以计算倒数第二项的模糊值(设为a)
- 且m足够大时,(m-1)/m>=0.618
- 需要注意:在m值较大时,(m-1)/m即便很接近0.618,但m值太大,因此0.618*m得到的模糊值也会有较大误差,所以需要a++直到找到最适合的前两项
- 上一点注意的详细公式是:小于两倍的sqrt(n)。
1 //斐波拉契-卢卡斯数列 2 //Memory 1100 K,Time: 234 Ms 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 using namespace std; 8 9 #define INF 0x3f3f3f3f 10 11 int m1,m2; //让第二项最小的初始两项 12 13 //计算初始两项并刷新最适合的m1,m2 14 void compute(int a,int b,int t) 15 { 16 while(t <= a && t >= 1) 17 { 18 b = a; 19 a = t; 20 t = b - a; 21 } 22 if(m2 > b) 23 { 24 m1 = a; 25 m2 = b; 26 } 27 } 28 29 int main() 30 { 31 int T,n; 32 scanf("%d",&T); 33 34 while(T--) 35 { 36 int a,t; 37 scanf("%d",&n); 38 a = (int)(0.618*n)-1; //倒数第二项模糊值 39 40 m1 = m2 = INF; 41 int i = -1; 42 while(a+(++i) <= n && i <= (int)2*sqrt(n)) //倒数第二项小于最后一项,且次数小于2*sqrt(n) 43 { 44 compute(a+i,n,n-a-i); 45 } 46 47 printf("%d %d\n",m1,m2); 48 } 49 50 return 0; 51 }
上述Code的 i <= (int)2*sqrt(n)的不等式是小编试出来的,测试数据在这些次数内可以过,如果不加的话,肯定是TLE的。
大家如果有更加合适的Code可以写在评论里面(⊙o⊙)哦~,小编太渣了,没有更加清楚明白的思路= =
Fighting~
他坐在湖边,望向天空,她坐在对岸,盯着湖面


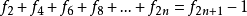
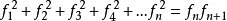

 浙公网安备 33010602011771号
浙公网安备 33010602011771号