算法第三章作业2

Chapter3 动态规划

动态规划的基本思想

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划法求解的问题，经分解得到的子问题往往不是互相独立的。

$ 多阶段图最短路问题$

下图表示城市之间的交通路网，线段上的数字表示费用，单向通行由 $ 。求的最省费用。$

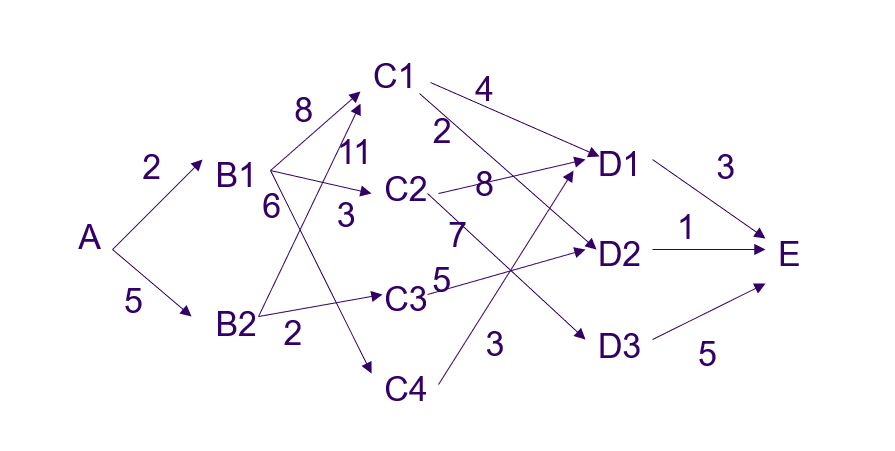
此图有明显的次序，可以划分为5阶段。故此问题的要求是：在各个阶段选取一个恰当的决策，使由这些决策组成的一个决策序列所决定的一条路线，其总路程最短。

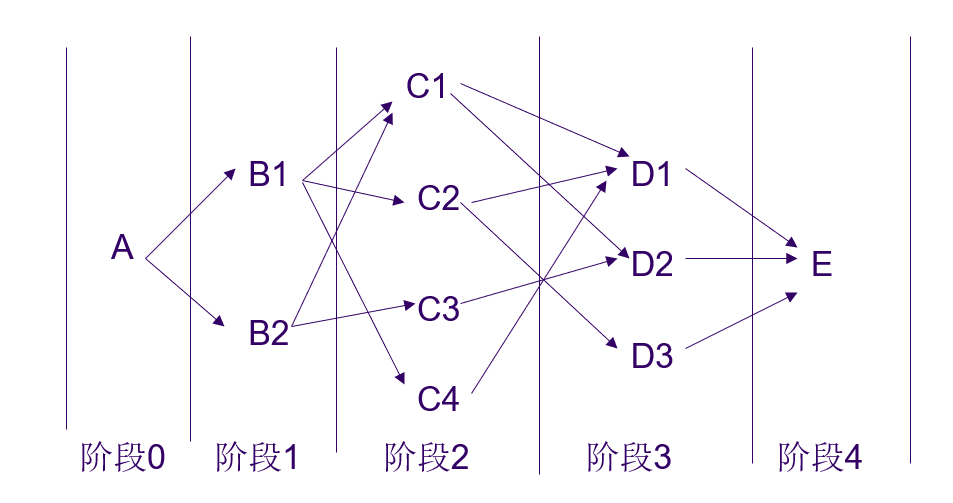
分析：如果 $ 的最短路已知，的最短路已知知道了最短路$

所以，动态规划有以下两个特点

原问题的最优解包含了子问题的最优解 $ 最优子结构$
求解 $ 问题时$
- $ 问题依赖的最优解$
- $ 问题依赖的最优解$

可以看出， $ 的解被重复使用，子问题的解被多次使用子问题重叠重复计算$

设计问题的步骤

找出最优解的性质，刻画其结构特征
递归的定义最优值
以自底向上的方式计算它
根据计算最优值时得到的信息，构造最优解

定义递归函数注意要点

传的参数，以及它的范围条件
递归的边界条件，通常在记忆化搜索中，以记录的元素存在为边界条件

 if(Memorized[i][j]) return Memorized[i][j];

剪枝的条件

矩阵连乘问题

$ 给定个矩阵：，其中与是可乘的。确定一种连乘的顺序，使得矩阵连乘的计算量为最小。$

如果直接顺序相乘，矩阵连乘的基本乘法数是

可以发现，在矩阵很多时，乘法的数目是很庞大的，因此，我们需要最小化乘法的次数来减少计算的时间。

不同计算顺序的差别

可以发现：求多个矩阵的连乘积时，计算的结合顺序是十分重要的。

考虑一种四个矩阵相乘的特殊情况

设矩阵为 $ ，的行列为的行列为以此类推.$

这样，四个矩阵的行列值，可以通过一个一维数组存放.

 int p[5] = {p0,p1,p2,p3,p4};

根据上表的计算顺序对于乘法次数的影响我们可以发现，乘法次数的大小取决于加的括号的位置，于是，我们可以对 $ 这四个矩阵的乘法顺序进行划分，有以下三种情况$

现在要做的工作就是，如果求出了 $ ，，，这四个子问题的乘法次数的最小值，再把它们三种情况进行比较，就求得了整个问题的最小值.$

如果设 $ 是矩阵的值，那么，上述三个的乘法次数如下$

通过观察，我们可以归纳出从 $ 到的通用方程$

从 $ 到的通用方程$

设矩阵 $, 是划分的位置$
- $$
- $$

备忘录

使用 $ 记录已经求过的子问题，避免了相同子问题的重复计算$

递归求解

 #include <bits/stdc++.h>
 
 using namespace std;
 #define ll long long
 #define mod 1000000007
 const ll maxn = 2e6 + 7;
 ll p[maxn];
 ll m[1000][1000];
 
 ll recursiveMatrixChain(ll i, ll j) {
     if (i == j) return  m[i][j]=0;
     if (m[i][j] > 0) return m[i][j];
     ll minVal = recursiveMatrixChain(i, i) + recursiveMatrixChain(i + 1, j) + p[i - 1] * p[i] * p[j];
     m[i][j] = minVal;
     for (long long k = i ; k < j; ++k) {
         ll tmp = recursiveMatrixChain(i, k) + recursiveMatrixChain(k + 1, j) + p[i - 1] * p[k] * p[j];
         if (tmp < minVal) {
             minVal = tmp;
        }
    }
     m[i][j] = minVal;
     return minVal;
 }
 
 
 int main() {
     ll n;
     cin >> n;
     for (long long i = 0; i <= n; ++i) {
         cin >> p[i];
    }
     int ans=recursiveMatrixChain(1, n);//注意范围，因为题目给定的n是矩阵数目-1所以是n
     //如果题目了n个矩阵，那么递归的范围是[1,n-1]
 //   RecurMatrixChain(1,n);
 //   for (long long i = 0; i <= n; ++i) {
 //       for (long long j = 0; j <= n; ++j) {
 //           cout << m[i][j] << setw(5) << " ";
 //       }
 //       cout << '\n';
 //   }
     cout<<ans;
 
     return 0;
 }

循环求解

如何避免递归？

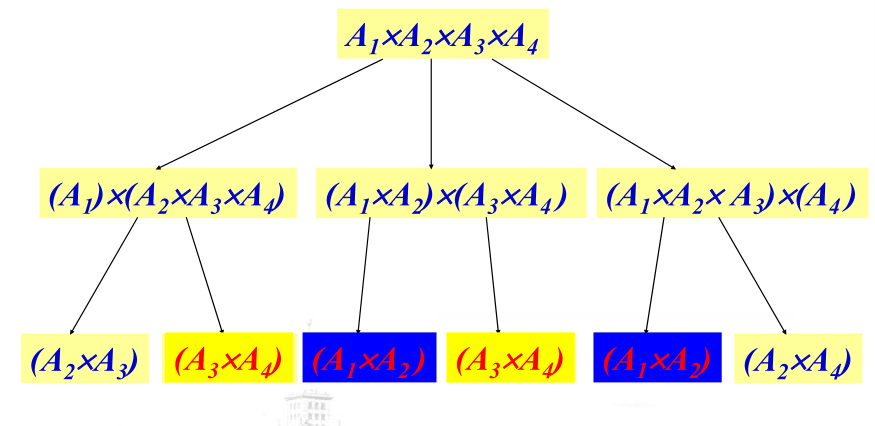
可以发现，递归是自顶向下的求解过程，如果我们换一种思路，从树底求解最小子问题（两个矩阵连乘的问题），再用求解好的子问题求解更上层的问题，最终达到求解1-n整个问题答案的目的

时间复杂度为： $$

空间复杂度为： $$

Code

 #include <bits/stdc++.h>
 
 using namespace std;
 #define ll long long
 #define mod 1000000007
 const ll maxn = 2e6 + 7;
 int m[2000][2000];
 int p[2000];
 int s[2000][2000];
 int n;
 
 int matrixChain() {
     for (long long i = 0; i <= n; ++i) {
         //对角线上的元素置0
         m[i][i] = 0;
    }
     for (long long i = n; i >= 1; --i) {
         for (long long j = i + 1; j <= n; ++j) {
             //找出每一个的初值
             m[i][j] = m[i][j] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
             s[i][j] = i;
             for (long long k = i + 2; k < j; ++k) {//i+1已经比过
                 //找到最小值
                 int tmp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                 if (tmp < m[i][j]) {
                     m[i][j] = tmp;
                     s[i][j] = k;
                }
            }
        }
    }
     return m[1][n];
 }
 
 void trace(int i, int j) {
     if (i == j) {
         cout << 'A' << i;
         return;
    }
     cout << "(";
     int k = s[i][j];
     trace(i, k);
     trace(k + 1, j);
     cout << ")";
     return;
 }
 
 
 int main() {
 
     cin >> n;
     for (long long i = 0; i <= n; ++i) {
         cin >> p[i];
    }
     cout << matrixChain() << endl;
     trace(1, n);
     cout << endl;
     for (long long i = 0; i <= n; ++i) {
         for (long long j = 0; j <= n; ++j) {
             cout << m[i][j] << ' ';
        }
         cout << '\n';
    }
     return 0;
 }

路径问题

问题集

数字三角形

https://www.luogu.com.cn/problem/P1216

 #include <bits/stdc++.h>
 
 using namespace std;
 #define ll long long
 #define mod 1000000007
 const ll maxn = 2e6 + 7;
 int dp[1001][1001];
 
 int main() {
     ll n;
     cin >> n;
     for (long long i = 0; i <= n; ++i) {
         for (long long j = 0; j <= n; ++j) {
             dp[i][j] = -1000000;
        }
    }
     for (long long i = 1; i <= n; ++i) {
         for (long long j = 1; j <= i; ++j) {
             cin >> dp[i][j];
        }
    }
     for (long long i = n - 1; i >= 1; --i) {
         for (long long j = 1; j <= i; ++j) {
             dp[i][j] += max(dp[i + 1][j], dp[i + 1][j + 1]);
        }
    }
 //   for (long long i = 0; i <= n; ++i) {
 //       for (long long j = 0; j <= n; ++j) {
 //           cout << dp[i][j] << ' ';
 //       }
 //       cout << endl;
 //   }
     cout << dp[1][1];
 
 
     return 0;
 }

滑雪

https://www.luogu.com.cn/problem/P1434

记忆化DFS

 #include <bits/stdc++.h>
 
 using namespace std;
 #define ll long long
 #define mod 1000000007
 const ll maxn = 2e6 + 7;
 ll dx[4] = {1, -1, 0, 0};
 ll dy[4] = {0, 0, 1, -1};
 ll a[1001][1001];
 ll s[1001][1001];
 ll r, c;
 
 ll dfs(ll x, ll y) {
     if (s[x][y]) return s[x][y];
     s[x][y] = 1;
     for (long long i = 0; i < 4; ++i) {
         ll xi = x + dx[i];
         ll yi = y + dy[i];
         if (xi > 0 && yi > 0 && xi <= r && yi <= c && a[x][y] > a[xi][yi]) {
             //这里的边界有效条件除了考虑xi,yi的不能超范围，还要保证已经搜过的不能再搜的边界条件，也就是a[x][y] > a[xi][yi]
             dfs(xi, yi);
             s[x][y] = max(s[x][y], s[xi][yi] + 1);
        }
    }
     return s[x][y];
 }
 
 int main() {
     ios::sync_with_stdio(false);
     cin.tie(0);
     cin >> r >> c;
     for (long long i = 1; i <= r; ++i) {
         for (long long j = 1; j <= c; ++j) {
             cin >> a[i][j];
        }
    }
     ll ans = -1;
     for (long long i = 1; i <= r; ++i) {
         for (long long j = 1; j <= c; ++j) {
             ans = max(ans, dfs(i, j));
        }
    }
     cout << ans << endl;
 //   for (long long i = 0; i <= r; ++i) {
 //       for (long long j = 0; j <= c; ++j) {
 //           cout << s[i][j] << ' ';
 //       }
 //       cout << endl;
 //   }
     return 0;
 }

最长公共子序列（LCS）

若给定序列 $ ，则另一序列，是的子序列是指存在一个严格递增下标序列使得对于所有有：。$

例如，序列 $，，，是序列，，，，，，的子序列，相应的递增下标序列为，，，。$

给定 $ 个序列和，当另一序列既是的子序列又是的子序列时，称是序列和的公共子序列。$

给定 $ 个序列和，找出和的最长公共子序列。$

LCS的结构分析

设序列 $ 和的最长公共子序列为，则 (1)若，则，且是和的最长公共子序列。 (2)若且 $

由此可见，2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此，最长公共子序列具有最优子结构性质（2，3条件下总有一个最优解）。

由LCS 的最优子结构性质建立子问题最优值的递归关系。用 $ 记录序列和的最长公共子序列的长度。其中，；。当或时，空序列是和的最长公共子序列。故此时。其它情况下，由最优子结构性质可建立递归关系如下：$

可以发现

这是一个二维表
填表顺序从左上角到右下角
时间复杂度和空间复杂度都为 $$

同时LCS还具有子问题的重叠性

算法思路

自左而右自上而下建立表格 $ 。 (1)如果＝则将左上角元素值加1赋值给，如果本身是最左上角元素就为1。 (2)如果不等于则该点元素值取－和－中较大的一个。如果＝且＝（最左上角）则取$

Code

 #include <bits/stdc++.h>
 
 using namespace std;
 #define ll long long
 #define mod 1000000007
 const ll maxn = 2e6 + 7;
 int c[2000][2000];
 
 void LCSLength(char x[], char y[]) {  //调用该函数前，先将c数组置初值为0
     int i, j;
     for (i = 1; i <= strlen(x); i++) //自上而下
         for (j = 1; j <= strlen(y); j++) { //每行自左向右
             if (x[i - 1] == y[j - 1])//下标从0开始
                 c[i][j] = c[i - 1][j - 1] + 1;
             else if (c[i - 1][j] >= c[i][j - 1]) {
                 c[i][j] = c[i - 1][j];
            } else c[i][j] = c[i][j - 1];
        }
 }
 
 void LCS(int i, int j, char x[], char y[]) {
     if (i == 0 || j == 0) {
         return;
    }
     if (x[i - 1] == y[j - 1]) {//下标从0开始
         LCS(i - 1, j - 1, x, y);
         cout << x[i - 1];//下标从0开始
    } else if (c[i - 1][j] >= c[i][j - 1]) {
         LCS(i - 1, j, x, y);
    } else LCS(i, j - 1, x, y);
 }
 
 
 char x[12000];
 char y[12000];
 
 int main() {
     cin >> x >> y;
     LCSLength(x, y);
     int lenx = strlen(x);
     int leny = strlen(y);
 
     cout << c[lenx][leny] << endl;
 
     for (long long i = 0; i <= max(lenx, leny); ++i) {
         for (long long j = 0; j <= max(lenx, leny); ++j) {
             cout << c[i][j] << ' ';
        }
         cout << endl;
    }
 
     LCS(lenx, leny, x, y);
 
     return 0;
 }
 /*
 dabcfbc eabfcab
  */

posted @ 2020-11-03 15:35 幼儿算数阅读(96) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

幼儿算数