NOIP 2025 题解

我草彻底怒了，NOIP 怎么是四道棒棒糖题，我必须立刻接受自己只有普二水平的事实，并且立刻加训。

---

candy

考虑对于每种糖果，拆成若干权重为 \(2\) 价格为 \(a + b\) 的糖果，与 \(0/1\) 个权重为 \(1\) 价格为 \(a\) 的糖果，然后考虑先全选权重为 \(2\) 的再从小往大贪心删。

sale

考虑刻画不合法条件，发现：

• 贪心策略一定是，选一个性价比最高的前缀，然后可能加上一个单点，并且那个单点如果脱离了前缀那么现价一定是 \(1\)。
  那么可能可能出现贪心不优当且仅当：
  • 新加的与前缀脱离的一个糖果，与现价为 \(1\) 且原价最小的糖果一起，换成原价最大且未选的现价为 \(2\) 的糖果更优。
  • 或是没有与前缀脱离的一个糖果，但是钱没用完，且现价为 \(1\) 且原价最小的糖果换成原价最大且未选的现价为 \(2\) 的糖果更优，后面我们会说明这一情况几乎无需特殊处理。

考虑按原价排序，枚举最后一个现价为 \(1\) 的糖果和被替换的糖果，发现有几段：

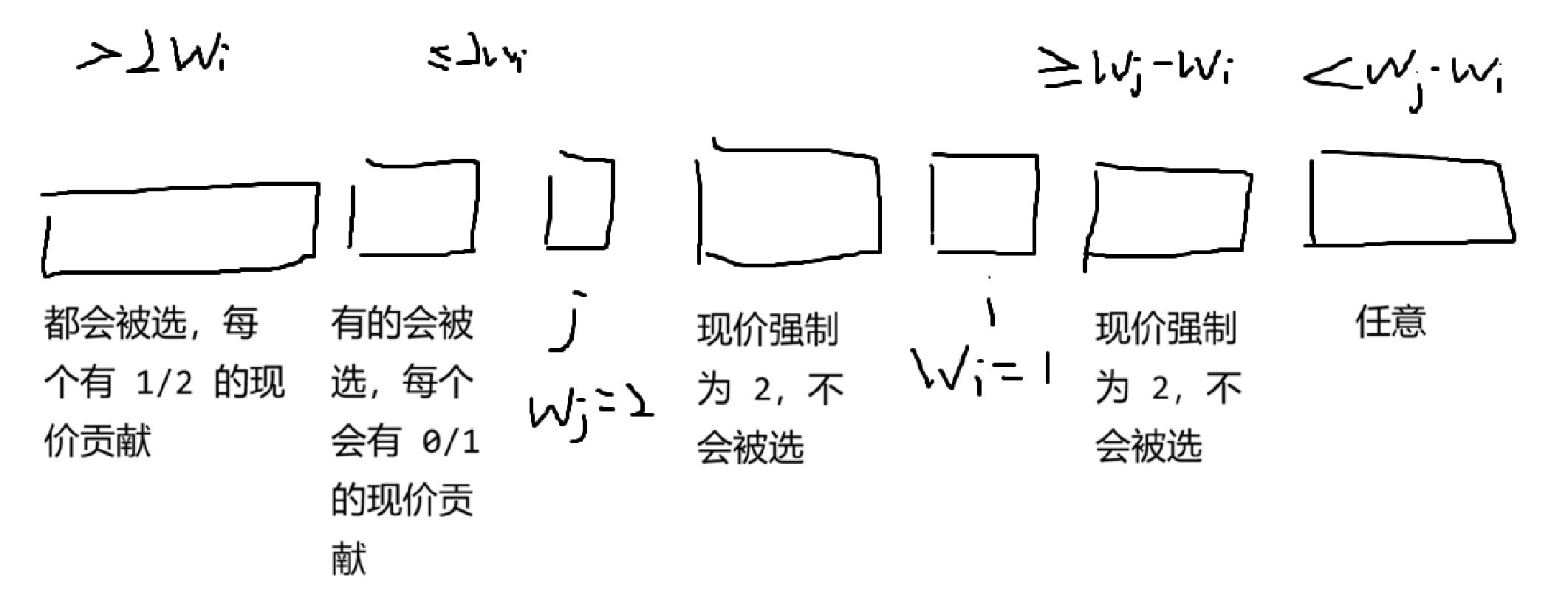
按这个随便算一下组合数就是 \(O(n^2)\) 的。

tree

考虑朴素 dp，设计状态需要子树 \(\operatorname{mex}\) 和贡献到祖先的点的个数，可以 \(O(n^3)\)。
转移相当于先取所有子树 \(\operatorname{mex}\) 的 \(\max\) 再分配有多少个点会对当前结点 \(\operatorname{mex}\) 有贡献，于是我们可以把取 \(\max\) 改为任选一个儿子继承 \(\operatorname{mex}\)。
一个点的贡献为祖先链上最长且连续的“继承关系”，据此可以以当前连续继承关系个数与最长连续继承关系个数为状态设计 \(O(nm^2)\) dp。
考虑 \(O(m)\) 的两维，确定一维之后另一维有用的只有子树深度种，具体的当“当前连续继承关系个数”加上“子树最大深度”仍不大于“最长连续继承关系个数”时考虑“当前连续继承关系个数”就没有用了。
于是可以长链优化 dp，从长链转移可以简单打全局加 tag，不再赘述。

query

考虑部分分，\(L_i > \dfrac{n}{2}\) 是干啥的？发现此时两个端点之一一定距离询问点不超过 \(\dfrac{n}{2}\)（废话），但是以这个端点向一端伸出的所有长度在 \([L_i, R_i]\) 范围内的区间都合法。
这个可以推广到 \(R_i \le 2L_i\) 的情况，直接就可以 \(O(nm \log n)\) 了，进一步的，考虑预处理二的整数次幂之间的答案，两边就可以 \(O(n)\) 算了，复杂度 \(O(nm + n \log^2 n)\)。