AGC008 题解

A - Simple Calculator
B - Continguous Repainting
C - Tetromino Tiling
D - K-th K
E - Next or Nextnext
F - Black Radius

A - Simple Calculator

发现：

每次 \(x \gets x + 1\) 只会让 \(|x|\) 变化至多 \(1\)；
我们可以调整操作次序，使得 \(x \gets x + 1\) 的操作是被连续执行的（考虑 \(x \gets x + 1\)，\(x \gets -x\)，\(x \gets x + 1\) 与 \(x \gets -x\) 等价）；
不会连续执行两次 \(x \gets -x\)。

因此最优操作序列一定形如，先选择是否执行 \(x \gets -x\)，再执行若干次 \(x \gets x + 1\)，最后选择是否执行 \(x \gets -x\)，可以枚举四种情况避免分讨。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
ll Calc(int x, int y) { return x <= y ? y - x : 1e18; }
int main() {
	int x = Read(), y = Read();
	Write(min(min(Calc(x, y), Calc(x, -y) + 1), min(Calc(-x, y) + 1, Calc(-x, -y) + 2)));
}

B - Continguous Repainting

显然最终序列中至少有一个长度至少为 \(K\) 的颜色段，可以枚举这个颜色段，设为 \([i, i + K - 1]\)，而对于 \([1, i - 1]\) 的位置，考虑依次覆盖 \([1, K], [2, K + 1], \dots, [i - 1, i + K - 2]\)，\([i + K, N]\) 的位置同理，容易发现第 \(j\) 个位置的颜色仅由 \([j, j + K - 1]\) 这次覆盖的颜色决定，所以等价于 \([i, i + K - 1]\) 之外的位置的数可以任选。所以记录前缀和就可以轻松计算。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, k;
ll a[N], sum[2][N];
int main() {
	int i; n = Read(), k = Read();
	for(i = 1; i <= n; i++) a[i] = Read(), sum[0][i] = sum[0][i - 1] + a[i], sum[1][i] = sum[1][i - 1] + max(a[i], 0ll);
	ll ans = 0;
	for(i = 0; i + k <= n; i++) ans = max(ans, max(sum[0][i + k] - sum[0][i], 0ll) + sum[1][i] + sum[1][n] - sum[1][i + k]);
	Write(ans);
	return 0;
}

C - Tetromino Tiling

考虑放置 T、S、Z 字形时，总是会把剩下的某块区域（例如最左边的区域）的方格数变成奇数，从而不能放置剩下的图形（都是由四个方格组成）。
O 字形显然全部放置最优，考虑 L、J、I 字形都能两个两个的放置，同时 L、J、I 字形各取一个还能组成一个长为 \(6\)，宽为 \(2\) 的长方形，形象的，我们称之为“沙发形”。
而如果使用了两个“沙发形”，我们可以将 L、J、I 字形两两配对，一定不劣，所以我们只需考虑“沙发形”为 \(0\) 或 \(1\) 个的情况即可。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
int main() {
	int i; ll a[7], ans = 0;
	for(i = 0; i < 7; i++) a[i] = Read();
	ll r1 = a[3] / 2ll * 2ll + a[4] / 2ll * 2ll + a[0] / 2ll * 2ll, r2 = ((a[3] && a[4] && a[0]) ? ((a[3] - 1) / 2ll * 2ll + (a[4] - 1) / 2ll * 2ll + 3ll + (a[0] - 1) / 2ll * 2ll) : 0ll);
	ans = a[1] + max(r1, r2), Write(ans);
	return 0;
}

D - K-th K

我们将 \(\{x_i\}\) 排序，然后从左到右贪心插入 \(x_i\) 最小的 \(i\)，使得插入前数 \(i\) 的个数小于 \(i\) 个。剩下的数就可以任意插了，贪心正确性还是比较显然的。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const int N = 505;
int n, a[N * N], rk[N];
queue<int> need, res;
pair<int, int> x[N];
int main() {
	int i, j, k;
	n = Read();
	for(i = 1; i <= n; i++) x[i].first = Read(), x[i].second = i;
	sort(x + 1, x + n + 1);
	for(i = 1; i <= n; i++) {
		for(j = 1; j < x[i].second; j++) need.emplace(x[i].second);
		rk[x[i].second] = i;
	}
	for(i = j = 1; i <= n; i++) {
		while(j < x[i].first) {
			if(!need.empty()) a[j++] = need.front(), need.pop();
			else if(!res.empty()) a[j++] = res.front(), res.pop();
			else printf("No"), exit(0);
		}
		if(need.empty() || rk[need.front()] > i) {
			a[j++] = x[i].second;
			for(k = x[i].second + 1; k <= n; k++) res.emplace(x[i].second);
		}
		else printf("No"); exit(0);
	}
	while(j <= n * n) a[j++] = res.front(), res.pop();
	printf("Yes\n");
	for(i = 1; i <= n * n; i++) Write(a[i]), putchar(' ');
	return 0;
}

E - Next or Nextnext

对于 \(\{p_i\}\)，我们连接 \(N\) 条 \((i, p_i)\) 的有向边，构成图 \(G\)，由经典结论可知，\(G\) 中一定形成若干个环，在本题中，每个环的答案是独立的。而对于题目中的 \(\{a_i\}\)，我们同样连接 \(N\) 条 \((i, a_i)\) 的有向边，构成图 \(G'\)，由经典结论可知，\(G'\) 一定是一个内向基环树森林。
现在我们对于每个点，需要钦定 \(a_i\) 的值是 \(p_i\) 还是 \(p_{p_i}\)。也就相当于在图上是走一步还是走两步。
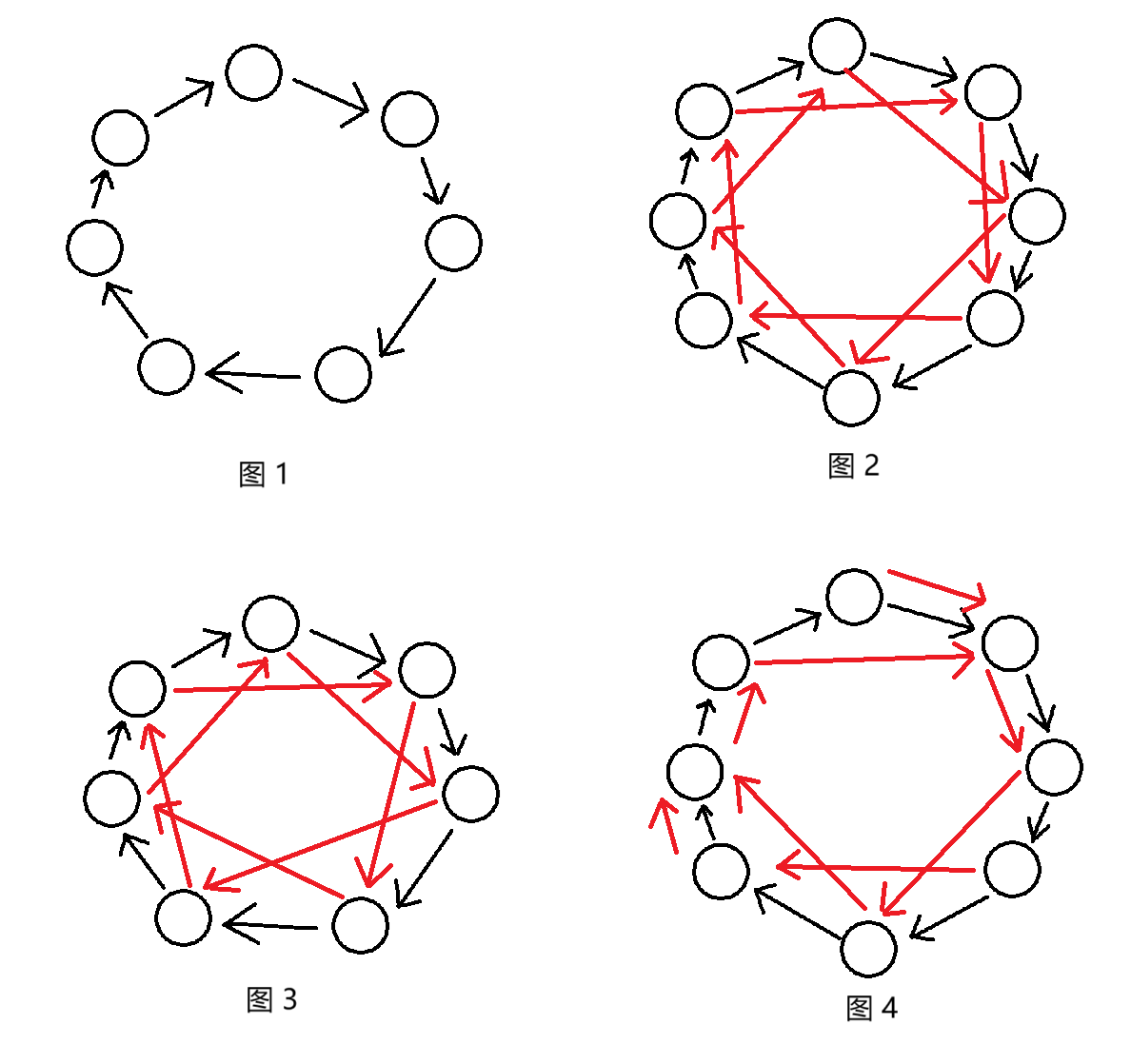
分类讨论（黑色边表示 \((i, p_i)\)，红色边表示 \((i, a_i)\)）：

图 \(1\) 表示环上所有 \(a_i = p_i\)，环的结构不变；
图 \(2\) 表示环上所有 \(a_i = p_{p_i}\)，且环长为偶数，此时 \(G'\) 中会分裂成两个环；
图 \(3\) 表示环上所有 \(a_i = p_{p_i}\)，且环长为奇数，此时 \(G'\) 中环长不变，但连接方式发生了改变；
图 \(4\) 表示其他情况，此时所有环上的点在 \(G'\) 中仍然弱联通，且构成一棵内向基环树。

对于 \(G'\) 中的环，显然不同环长的环答案互不影响（对应图 \(1, 2, 3\)），设环长为 \(x\)，个数为 \(y\)：

枚举有多少个环对应图 \(2\) 的情况，设有 \(2z\) 个环，则选择 \(z\) 对的方案为 \(\dbinom{y}{2z} f(z)\)，其中 \(f(z)\) 表示从 \(2z\) 个数中选择 \(z\) 对的方案数，考虑最后一个的配对情况，易得递推式 \(f(z) = f(z - 1) \cdot (2z - 1)\)，再考虑每对之间的环可以旋转着拼上去，又会有 \(x^z\) 的贡献。
对于剩下的每个环，若 \(x \bmod 2 = 1\) 且 \(x > 1\)，则有两种方案，否则只有一种（对于 \(x = 1\) 而言，图 \(1, 3\) 无法区分）。

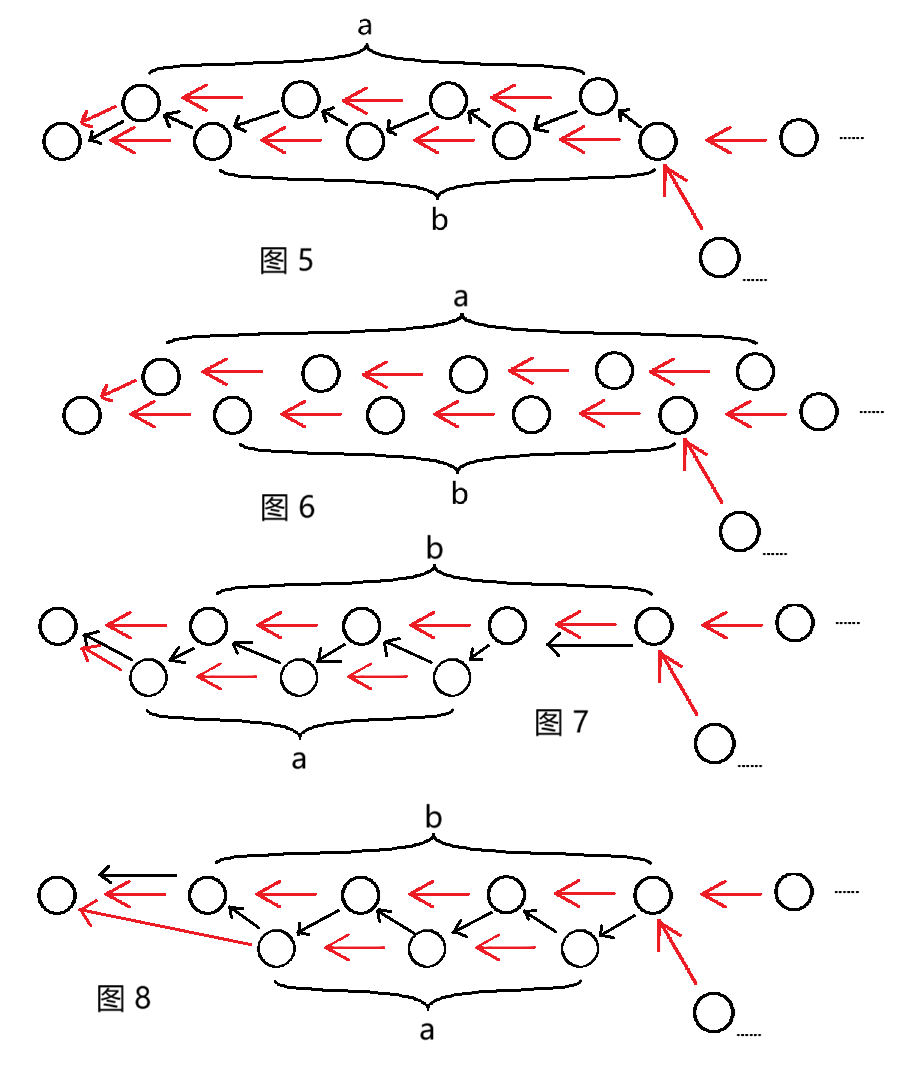
对于 \(G'\) 中的基环树，先来证明一个结论：每个基环树中，环上结点只有可能挂一条链。

证明：考虑 \(G'\) 中每个结点的入度至多为 \(2\)，而由 \(G\) 钦定 \(G'\) 中的环上结点之后，考虑非环上结点的前一个一定是环上结点，否则一定有一个 \(a_i\) 是 \(i\) 沿着 \(p_i\) 跳至少三次的结果，不合法，所以非环上结点的入度至多为 \(1\)。

由上我们还可以得出，一个非环上结点 \(y\) 的前驱 \(x\) 一定满足 \(p_{p_x} = y\)，所以手玩一下发现（记链长为 \(a\)，链挂在的“分叉点”距下一个“分叉点”的距离为 \(b\)）：

对于 \(a = b\) 的情况，如图 \(5\)，恰有 \(1\) 种解；
对于 \(a > b\) 的情况，如图 \(6\)，一定不合法；
对于 \(a < b\) 的情况，如图 \(7, 8\)，恰有 \(2\) 种解。

所以我们把环的情况和基环树的情况拼起来就可以了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
	int sig = 1; ll num = 0; char c = getchar();
	while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
	while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
	return num * sig;
}
void Write(ll x) {
	if(x < 0) putchar('-'), x = -x;
	if(x > 9) Write(x / 10);
	putchar((x % 10) ^ 48);
}
const ll Mod = 1e9 + 7;
const int N = 100005;
int n, a[N], cir[N];
bool vis[N];
vector<int> vec[N];
ll fact[N], invfact[N], ans = 1;
ll QuickPow(ll x, ll y) {
	ll res = 1ll;
	while(y) {
		if(y & 1) res = res * x % Mod;
		x = x * x % Mod, y >>= 1;
	}
	return res;
}
ll C(ll x, ll y) { if(x < y || y < 0) return 0; return fact[x] * invfact[y] % Mod * invfact[x - y] % Mod; }
int main() {
	int i, j; n = Read(), fact[0] = invfact[0] = 1;
	for(i = 1; i <= n; i++) fact[i] = fact[i - 1] * i % Mod, invfact[i] = QuickPow(fact[i], Mod - 2), a[i] = Read(), vec[a[i]].emplace_back(i);
	for(i = 1; i <= n; i++) {
		if(vec[i].size() > 2) printf("0"), exit(0);
		if(vec[i].size() == 2) {
			int l1 = 1, l2 = 1, x = vec[i][0], y = vec[i][1];
			while(vec[x].size() == 1) vis[x] = true, x = vec[x][0], l1++;
			while(vec[y].size() == 1) vis[y] = true, y = vec[y][0], l2++;
			if(vec[x].size() == 2 && vec[y].size() == 2) printf("0"), exit(0);
			if(vec[x].size() == 2) swap(l1, l2);
			if(l1 > l2) printf("0"), exit(0);
			if(l1 < l2) ans = ans * 2ll % Mod;
			vis[i] = true, vis[x] = true, vis[y] = true;
		}
	}
	for(i = 1; i <= n; i++) {
		int j = i, cnt = 0;
		if(vis[j]) continue;
		while(!vis[j]) {
			if(vec[j].empty()) printf("0"), exit(0);
			vis[j] = true, j = vec[j][0], cnt++;
		}
		cir[cnt]++;
	}
	ll d = 1, res = 0;
	for(j = 0; j <= cir[1]; j += 2) res = (res + d * C(cir[1], j) % Mod) % Mod, d = d * (j + 1) % Mod;
	ans = ans * res % Mod;
	for(i = 2; i <= n; i++) {
		ll d = 1, res = 0;
		for(j = 0; j <= cir[i]; j += 2) res = (res + 1ll * (i % 2 == 0 ? 1ll : QuickPow(2ll, cir[i] - j)) * QuickPow(i, j / 2) % Mod * d % Mod * C(cir[i], j) % Mod) % Mod, d = d * (j + 1) % Mod;
		ans = ans * res % Mod;
	} 
	Write(ans), putchar('\n');
	return 0;
}

F - Black Radius

我们令距 \(u\) 的距离不超过 \(d\) 的点集为 \(S_{u, d}\)，如图 \(1\) 即为 \(S_{u, 3}\)，图 \(2\) 即为 \(S_{u, 4}\)。

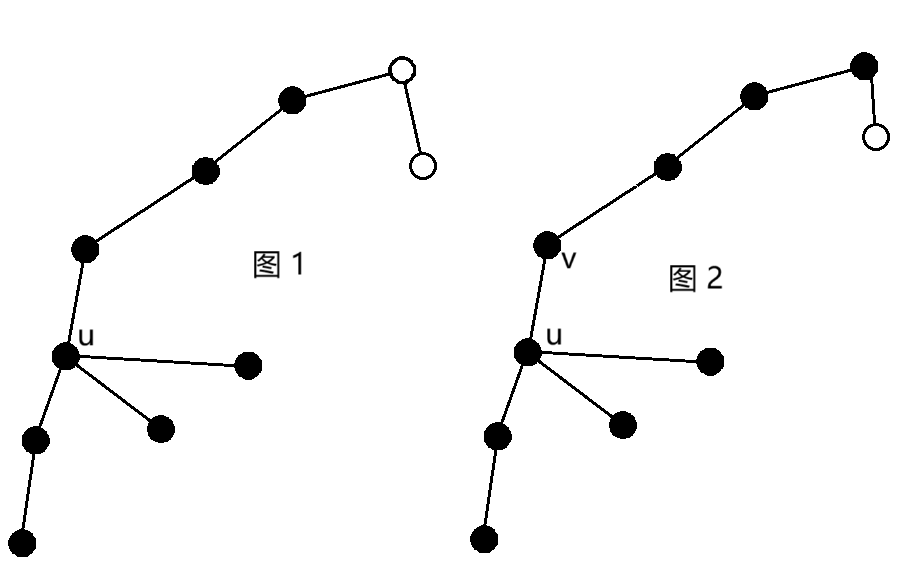
考虑如何补充不漏的计数，一般来说对于多个结果一致的方案，我们只会统计最优方案。本题中，对于相同的 \(S_{u, d}\)，我们取 \(d\) 最小的那个，此时，对于与 \(u\) 相邻的 \(v\)，必有 \(S_{v, d - 1} \not = S_{u, d}\)。我们来证明对于一个点集 \(S \not = \{1, 2, \dots, N\}\)，使 \(d\) 最小的 \(u\) 是唯一的。

证明：考虑有 \(v \not = u\) 且 \(S_{u, d} = S_{v, d}\)，令 \(\operatorname{dis}(u, v) = d'\)，由于 \(S \not = \{1, 2, \dots, N\}\)，必有一个点 \(w\) 使得 \(\operatorname{dis}(u, w) = \operatorname{dis}(v, w) = d\)，我们把树想象成 \(u, v\) 的路径上挂着若干棵子树的形式。若 \(w\) 挂在一棵根为 \(p\) 的子树上，且 \(dis(u, p) \not = dis(v, p)\)，显然矛盾，否则，\(d' \bmod 2 = 0\)，取 \(u, v\) 路径的中点 \(q\)，可以证明，对于 \(q\) 的子树外的点 \(w\)，\(\min(\operatorname{dis}(u, w), \operatorname{dis}(v, w)) \le d\)，容易有 \(d \ge d'\)，又因为 \(\operatorname{dis}(q, w) = \operatorname{dis}(u, q) - \operatorname{dis}(u, w)\) 和 \(\operatorname{dis}(q, w) = \operatorname{dis}(v, q) - \operatorname{dis}(v, w)\) 中的一个必然成立，所以 \(S_{q, d - \frac{d'}{2}} = S_{u, d} = S_{v, d}\)，即 \(S_{u, d}\) 不是最优情况。

我们发现若 \(S_{u, d}\) 是最优的，那么 \(S_{u, d - 1}\) 也是最优的，所以考虑找出上界，首先 \(S_{u, d}\) 不能覆盖所有的点，因此记 \(f_u\) 为若 \(u\) 为根，所有结点的最大深度，则 \(d < f_u\)。
再考虑 \(v\) 与 \(u\) 相邻且 \(S_{v, d - 1} = S_{u, d}\) 时，发现当且仅当以 \(u\) 为根的树中，\(S_{v, d - 1}\) 能把除以 \(v\) 为根的子树外的所有结点全覆盖（如上图的 \(S_{v, 3} = S_{u, 4}\)），否则 \(S_{u, d}\) 必然可以进一步覆盖，要使合法的 \(d\) 最大，必然令 \(v\) 为深度最大的那个子树，可以换根 dp。
现在的问题是，有些点不能作为初始的 \(x\)，这个时候我们还是在中心处 \(u\) 统计答案，考虑能够作为 \(x\) 的 \(v\)，那么 \(v\) 一定能通过向 \(u\) 走一步，再令 \(d\) 减一达到 \(d\) 的最小值。所以以 \(u\) 为根的树中，\(v\) 所在的以 \(u\) 的儿子为根的子树一定全部被覆盖，于是可以考虑选择深度最小的，且至少有一个子树内的结点能作为初始的 \(x\) 的子树，此时的子树的深度即为答案下界。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline ll Read() {
    int sig = 1; ll num = 0; char c = getchar();
    while(!isdigit(c)) { if(c == '-') sig = -1; c = getchar(); }
    while(isdigit(c)) num = (num << 3) + (num << 1) + (c ^ 48), c = getchar();
    return num * sig;
}
void Write(ll x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) Write(x / 10);
    putchar((x % 10) ^ 48);
}
const int N = 200005, inf = 1e9;
int n, a[N], g[N], siz[N];
ll ans = 0;
vector<int> e[N];
void Dfs(int u, int fa) { siz[u] = a[u]; for(auto v : e[u]) if(v != fa) Dfs(v, u), g[u] = max(g[u], g[v] + 1), siz[u] += siz[v]; }
void Dfs2(int u, int fa, int gfa) {
    int maxn = -1, secmaxn = -1, hminn = (siz[1] == siz[u] ? inf : gfa);
    for(auto v : e[u]) if(v != fa) {
        if(g[v] > maxn) secmaxn = maxn, maxn = g[v];
        else secmaxn = max(secmaxn, g[v]);
        if(siz[v]) hminn = min(hminn, g[v]);
    }
    for(auto v : e[u]) if(v != fa) Dfs2(v, u, max(g[v] == maxn ? secmaxn : maxn, gfa) + 1);
    if(gfa > maxn) secmaxn = maxn, maxn = gfa;
    else secmaxn = max(secmaxn, gfa);
    ans += max(min(maxn, secmaxn + 2) - (a[u] ? -1 : hminn), 0);
}
int main() {
    int i; n = Read();
    for(i = 1; i < n; i++) { int u = Read(), v = Read(); e[u].emplace_back(v), e[v].emplace_back(u); }
    for(i = 1; i <= n; i++) { char c = getchar(); while(!isdigit(c)) c = getchar(); a[i] = c ^ '0'; }
    Dfs(1, 0), Dfs2(1, 0, -inf), Write(ans + 1);
}

posted @ 2025-06-28 21:50 Include_Z_F_R_qwq 阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

IncludeZFR