AGC005 题解

目录

• A - STring
• B - Minimum Sum
• C - Tree Restoring
• D - ~K Perm Counting
• E - Sugigma: The Showdown
• F - Many Easy Problems

A - STring

用栈模拟一下即可，具体的，当栈顶出现形如 ST 时，将其弹出。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}

int main() {
	string s;
	cin >> s;
	stack<char> st;
	int i, n = s.size();
	for(i = 0; i < n; i++) {
		if(s[i] == 'T' && !st.empty() && st.top() == 'S') {
			st.pop();
		}
		else {
			st.emplace(s[i]);
		}
	}
	Write(st.size());
	return 0;
}

B - Minimum Sum

考虑将每个数的贡献拆开，从最小的数开始考虑，包括这个最小数的区间的最小值一定是该数，而剩下的区间正好被最小值拆成两半，可以递归地去做。
具体的，用 ST 表维护区间内最小值的位置，设这个最小值的位置为第 \(x\) 位，当前区间为 \([l, r]\)，则贡献为 \(a_x \cdot (r - x + 1) \cdot (x - l + 1)\)，再递归区间 \([l, x - 1]\) 及 \([x + 1, r]\)。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}

const int N = 200005, lgN = 20;
int n, a[N], lg[N];
void Init_lg() {
	int i;
	for(i = 2; i < N; i++) {
		lg[i] = lg[i >> 1] + 1;
	}
}
struct ST_Table {
	int f[lgN][N], g[lgN][N];
	void Init() {
		int i, j;
		for(i = 1; i <= n; i++) {
			f[0][i] = a[i], g[0][i] = i;
		}
		for(i = 1; i <= lg[n]; i++) {
			for(j = 1; j + (1 << i) - 1 <= n; j++) {
				if(f[i - 1][j] < f[i - 1][j + (1 << (i - 1))]) {
					f[i][j] = f[i - 1][j], g[i][j] = g[i - 1][j];
				}
				else {
					f[i][j] = f[i - 1][j + (1 << (i - 1))], g[i][j] = g[i - 1][j + (1 << (i - 1))];
				}
			}
		}
	}
	int Query(int l, int r) {
		int len = lg[r - l + 1];
		int x = f[len][l], y = f[len][r - (1 << len) + 1];
		return x < y ? g[len][l] : g[len][r - (1 << len) + 1];
	}
}st;
ll Solve(int l, int r) {
	if(l > r) {
		return 0;
	}
	int x = st.Query(l, r);
	return Solve(l, x - 1) + Solve(x + 1, r) + 1ll * (x - l + 1) * (r - x + 1) * a[x];
}
int main() {
	int i;
	n = Read();
	for(i = 1; i <= n; i++) {
		a[i] = Read();
	}
	Init_lg(), st.Init();
	Write(Solve(1, n));
	return 0;
}

C - Tree Restoring

回忆直径的定义，注意到 \(\max a_i\) 即为直径长度 \(d\)，因此我们先建出这个直径。
设直径的两个端点为 \(u, v\)，根据直径的性质，\(a_x = \max\{\operatorname{dis}(u, x), \operatorname{dis}(v, x)\}\)。
对于 \(d\) 的奇偶性分类讨论，对于 \(k\) 是偶数的情况，需要 \(\frac{d}{2} + 1 \sim d\) 的 \(a_i\) 各两个，\(\frac{d}{2}\) 的 \(a_i\) 一个；对于 \(k\) 是奇数的情况，需要 \(\frac{d + 1}{2} \sim d\) 的 \(a_i\) 各两个。于是 \(a_i\) 不够可以直接判无解。
对于剩下的点，我们可以在直径上挂着，可以证明，当 \(k\) 是偶数时，挂的点 \(a_i\) 的取值范围为 \([\frac{d}{2} + 1, d]\)；当 \(k\) 是奇数时，挂的点 \(a_i\) 的取值范围为 \([\frac{d + 3}{2}, d]\)。
注意特判 \(d = 1\) 的情况。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}

const int N = 105;
int n, a[N], cnt[N];

int main() {
	int i, d = 0;
	n = Read();
	for(i = 1; i <= n; i++) {
		int a = Read();
		d = max(d, a);
		cnt[a]++;
	}
	if(d == 1) {
		printf(n > 2 ? "Impossible" : "Possible");
		return 0;
	}
	for(i = d; i > d / 2; i--) {
		if(cnt[i] < 2) {
			printf("Impossible");
			return 0;
		}
	}
	if(d % 2 == 0 && cnt[d / 2] != 1) {
		printf("Impossible");
		return 0;
	}
	if(d & 1 && cnt[(d + 1) / 2] != 2) {
		printf("Impossible");
		return 0;
	}
	for(i = 1; i < (d + 1) / 2; i++) {
		if(cnt[i]) {
			printf("Impossible");
			return 0;
		}
	}
	printf("Possible");
	return 0;
}

D - ~K Perm Counting

直接统计很难做，考虑容斥。
首先我们画出一个 \(N \times N\) 的网格图，我们要在这个网格图上放 \(N\) 个棋子，棋子放在 \((i, j)\) 表示 \(P_i = j\)，那么问题转化为，每行每列只能放一个棋子，有若干个格子不能放，问方案数。
对于不能放的格子，我们若将其用红色格子表示（如下图所示，此图中 \(N = 10, K = 3\)），我们不难发现，这些格子构成一条斜线。

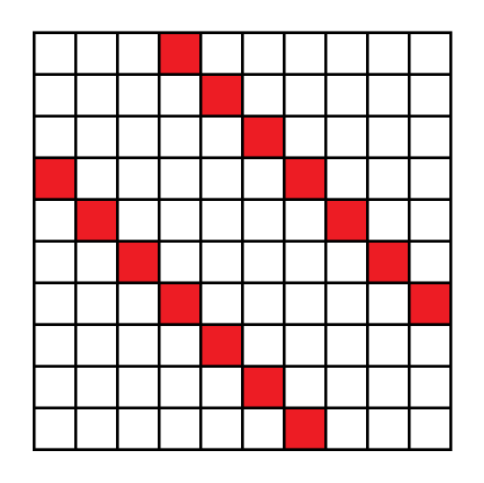
首先我们任意放置棋子，然后我们钦定 \(i\) 个棋子放置在红色格子上，其他格子任意放置，但要保证棋子互不冲突。
设我们将 \(i\) 个棋子放在红色格子里，且互不冲突的方案数为 \(f_i\)，由子集容斥我们可得答案为：

\[\sum_{i = 0}^N (-1)^i \cdot f_i \cdot (N - i)! \]

现在问题转化为如何求出 \(f_i\)，我们将有冲突的两个格子连线，得：

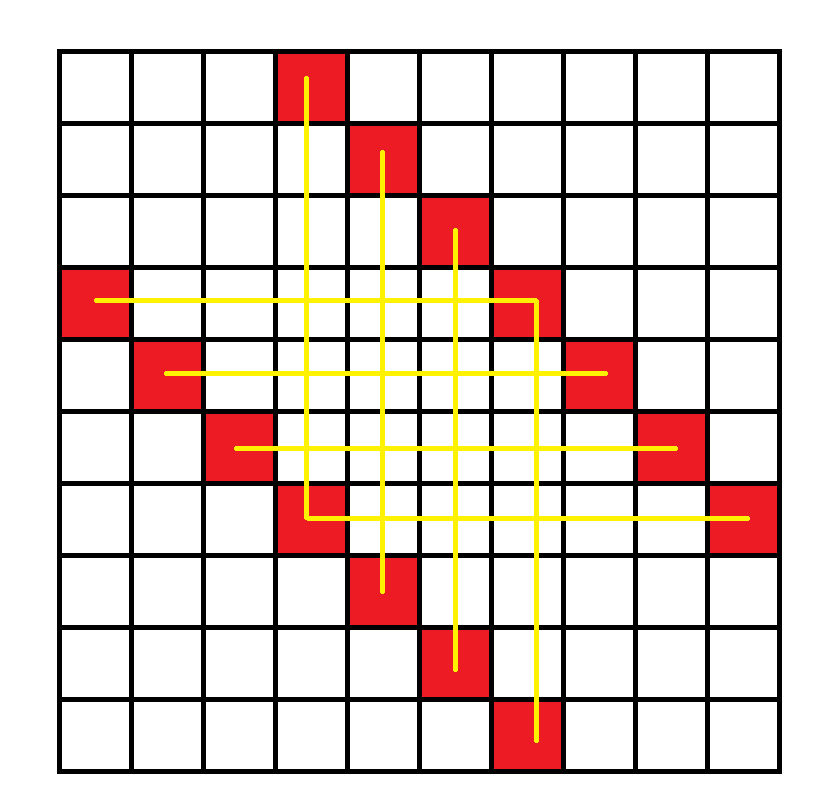
我们把格子看成结点，这样所有格子就形成了若干条链，因此，只有两个格子在一条链上相邻，这两个格子才冲突，不同链之间互不影响。
对于每一条链，“将 \(i\) 个棋子放在红色格子里，且互不冲突的方案数”可以通过 DP 简单求出，对于多条链的情况，只需简单合并即可。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}

const ll Mod = 924844033;
const int N = 2005;
int n, k, b, cnt[2];
ll g[2][2][N], h[2][N], f[2][N << 1], fact[N << 1];
ll QuickPow(ll x, ll y) {
	if(y == 0) {
		return 1;
	}
	if(y == 1) {
		return x;
	}
	ll half = QuickPow(x, y >> 1);
	if(y & 1) {
		return half * half % Mod * x % Mod;
	}
	return half * half % Mod;
}
int main() {
	n = Read(), k = Read();
	int m = 2 * (n - k);
	b = m / 2 / k;
	int i, j, p;
	for(i = 1; i <= min(k, m / 2); i++) {
		cnt[(m / 2 - i) / k + 1 - b] += 2;
	}
	bool o = 0;
	g[o][0][0] = h[0][0] = h[1][0] = 1;
	for(i = 1; i <= b + 1; i++) {
		for(j = 0; j <= i; j++) {
			g[o ^ 1][0][j] = (g[o][0][j] + g[o][1][j]) % Mod;
			if(j > 0) {
				g[o ^ 1][1][j] = g[o][0][j - 1];
			}
			h[1][j] = (h[1][j] + g[o ^ 1][1][j]) % Mod;
			if(i <= b) {
				h[0][j] = (h[0][j] + g[o ^ 1][1][j]) % Mod;
			}
		}
		o ^= 1;
	}
	o = 0, f[0][0] = 1;
	for(i = 0; i < 2; i++) {
		while(cnt[i]--) {
			for(j = 0; j <= b + i; j++) {
				for(p = 0; p + j <= m; p++) {
					f[o ^ 1][j + p] = (f[o ^ 1][j + p] + f[o][p] * h[i][j] % Mod) % Mod;
				}
			}
			for(p = 0; p <= m; p++) {
				f[o][p] = 0;
			}
			o ^= 1;
		}
	}
	fact[0] = 1;
	for(i = 1; i < (N << 1); i++) {
		fact[i] = fact[i - 1] * i % Mod;
	}
	ll ans = 0;
	for(i = 0; i <= n; i++) {
		ans = (ans + ((i & 1) ? Mod - 1ll : 1ll) * fact[n - i] % Mod * f[o][i] % Mod) % Mod;
	}
	Write(ans);
	return 0;
}

E - Sugigma: The Showdown

记先手走的树为红树，后手走的树为蓝树；在红树上，\(u, v\) 两点距离为 \(\operatorname{d}'(u, v)\)，在蓝树上，\(u, v\) 两点距离为 \(\operatorname{d}(u, v)\)。
首先我们考虑这样一个事实，对于红树上的一条边 \(e = (u, v)\)，若 \(\operatorname{d}(u, v) > 2\)，那么若当前是先手走，先手在 \(u\)，后手现在不在 \(u\) 或 \(v\)（记他当前所在的点为 \(x\)），先手可以通过以下策略来使游戏无法结束：

• 若 \(\operatorname{d}(u, x) > 1\)，原地不动；
• 否则走到 \(v\)，根据树的性质显然有 \(\operatorname{d}(v, x) \ge \operatorname{d}(u, v) - \operatorname{d}(u, x) > 2 - 1 = 1\)，后手无法一步抓到先手。

若红树上存在 \((u, v)\) 这条边，并且 \(\operatorname{d}(u, v) > 2\)，我们就称 \(u, v\) 均是“安全的”，因此我们只需要移动到“安全的”点就一定能使游戏无法结束。
现在我们只能在 \(\operatorname{d}(u, v) \le 2\) 的边 \(e = (u, v)\) 上走动了。

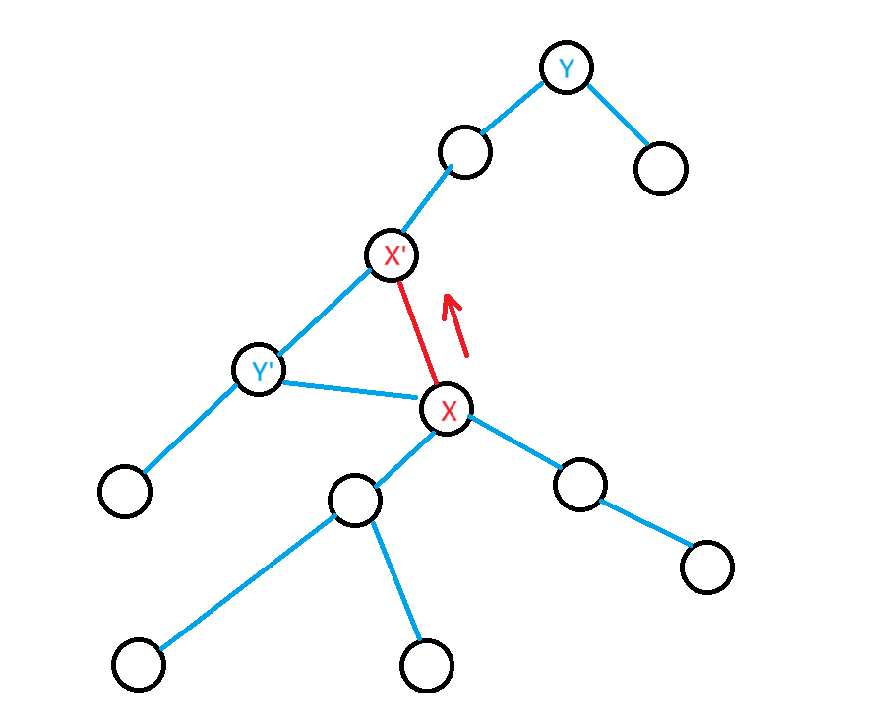
把蓝树的根定为 \(Y\)，一开始，\(X\) 一定在 \(Y\) 的子树内。
考虑当前后手走到 \(Y'\)，注意到当 \(X\)“跨过”\(Y'\)，并走到 \(X'\) 时，由于 \(\operatorname{d}(u, v) \le 2\) 的限制，后手一定能吃掉先手，显然不优。不如向下走，或干脆待在原地。
那么先手能走到 \(u\) 点，当且仅当 \(\operatorname{d}'(X, u) > \operatorname{d}(Y, u)\)，即先手能优先走到 \(u\)，我们称这个点是“可达的”。
直接遍历 \(X\) 能走到哪些“可达的”点，若其中有一个“安全的”点，那么可以走到那个点并判定游戏无法结束，否则走到"可达的”点中距 \(Y\) 最远的点即可，答案即为最大距离乘 \(2\)。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}

const int N = 200005, inf = 1e9;
int n, dis[2][N], f[N], ans;
vector<int> e[2][N];
void Dfs(bool b, int u, int fa) {
	f[u] = fa;
	for(auto v : e[b][u]) {
		if(v == fa) {
			continue;
		}
		dis[b][v] = dis[b][u] + 1, Dfs(b, v, u);
	}
}
bool Check(int u, int v) {
	if(dis[1][u] > dis[1][v]) {
		swap(u, v);
	}
	if(dis[1][u] == dis[1][v]) {
		return u == v || f[u] == f[v];
	}
	if(dis[1][u] + 1 == dis[1][v]) {
		return f[v] == u;
	}
	if(dis[1][u] + 2 == dis[1][v]) {
		return f[f[v]] == u;
	}
	return false;
}
void Dfs2(int u, int fa) {
	ans = max(ans, dis[1][u]);
	if(dis[1][u] <= dis[0][u]) {
		return ;
	}
	for(auto v : e[0][u]) {
		if(v == fa) {
			continue;
		}
		if(!Check(u, v)) {
			ans = inf;
		}
		Dfs2(v, u);
	}
}

int main() {
	int i, x, y;
	n = Read(), x = Read(), y = Read();
	for(i = 1; i < n; i++) {
		int u = Read(), v = Read();
		e[0][u].emplace_back(v), e[0][v].emplace_back(u);
	}
	for(i = 1; i < n; i++) {
		int u = Read(), v = Read();
		e[1][u].emplace_back(v), e[1][v].emplace_back(u);
	}
	Dfs(0, x, 0), Dfs(1, y, 0), Dfs2(x, 0);
	if(ans == inf) {
		printf("-1");
	}
	else {
		Write(ans * 2);
	}
	return 0;
}

F - Many Easy Problems

将树随便定一个根，记 \(x\) 的所有儿子构成的集合为 \(c_x\)，在 \(x\) 的子树内的点构成的集合为 \(t_x\)。
考虑对每个点计算贡献，对于点 \(x\) 和一个大小为 \(y\) 的点集 \(S\)，最小包含 \(S\) 的连通块不包括 \(x\) 当且仅当满足下面两个条件之一：

• \(\forall v \in S\)，\(\exists u \in c_x\)，\(v \in t_u\)；
• \(\forall v \in S\)，\(v \not \in t_x\)。

这样我们就得到了 \(x\) 对 \(f(y)\) 的贡献为：

\[\binom{N}{y} - \binom{N - |t_x|}{y} - \sum_{v \in c_x} \binom{|t_v|}{y} \]

因此：

\[f(y) = \sum_{x = 1}^N \binom{N}{y} - \binom{N - |t_x|}{y} - \sum_{v \in c_x} \binom{|t_v|}{y} \]

拆一下组合数，记满足 \(|t_x| = y\) 的 \(x\) 的个数与满足 \(N - |t_x| = y\) 的 \(x\) 的个数之和为 \(a_y\)：

\[\begin{aligned} f(y) &= \sum_{x = 1}^N \binom{N}{y} - \binom{N - |t_x|}{y} - \sum_{v \in c_x} \binom{|t_v|}{y} \\ &= N \cdot \binom{N}{y} - \sum_{x = y}^{N - 1} a_x \cdot \binom{x}{y} \\ &= N \cdot \binom{N}{y} - \sum_{x = y}^{N - 1} a_x \cdot \frac{x!}{y!(x-y)!} \\ &= N \cdot \binom{N}{y} - \frac{1}{y!} \sum_{x = y}^{N - 1} a_x x! \cdot \frac{1}{(x-y)!} \\ \end{aligned}\]

令 \(g(x) = a_x x!\)，\(h(x) = \dfrac{1}{x!}\)，则：

\[f(y) = N \cdot \binom{N}{y} - \frac{1}{y!} \sum_{x = y}^{N - 1} g(x) \cdot h(x-y) \]

再令 \(h'(x) = h(N - x)\)，可得：

\[f(y) = N \cdot \binom{N}{y} - \frac{1}{y!} \sum_{x = y}^{N - 1} g(x) \cdot h'(N-x+y) \]

这是一个很标准的卷积，用 NTT 做一下，并取序列的第 \(n + y\) 项就可以了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
	int sig = 1;
	ll num = 0;
	char c = getchar();
	while(!isdigit(c)) {
		if(c == '-') {
			sig = -1;
		}
		c = getchar();
	}
	while(isdigit(c)) {
		num = (num << 3) + (num << 1) + (c ^ 48);
		c = getchar();
	}
	return num * sig;
}
void Write(ll x) {
	if(x < 0) {
		putchar('-');
		x = -x;
	}
	if(x >= 10) {
		Write(x / 10);
	}
	putchar((x % 10) ^ 48);
}
const ll Mod = 924844033, g = 5;
const int N = 1000005;
int l, r[N];
ll a[N], b[N], ig;
ll QuickPow(ll x, ll y) {
	if(y == 0) {
		return 1;
	}
	if(y == 1) {
		return x;
	}
	ll half = QuickPow(x, y >> 1);
	if(y & 1) {
		return half * half % Mod * x % Mod;
	}
	return half * half % Mod;
}
void NTT(ll *a, int op) {
	int i, j, k;
	for(i = 0; i < (1 << l); i++) {
		if(i < r[i]) {
			swap(a[i], a[r[i]]);
		}
	}
	for(i = 1; i <= l; i++) {
		int mid = (1 << (i - 1));
		ll wn = QuickPow(op == 1 ? g : ig, (Mod - 1) / (mid << 1));
		for(j = 0; j < (1 << l); j += (mid << 1)) {
			ll w = 1;
			for(k = 0; k < mid; k++) {
				ll a1 = a[j + k], a2 = w * a[j + mid + k] % Mod;
				a[j + k] = (a1 + a2) % Mod, a[j + mid + k] = (a1 - a2 + Mod) % Mod;
				w = (w * wn) % Mod;
			}
		}
	}
}
int n, siz[N], cnt[N];
vector<int> e[N];
ll fact[N], invfact[N];
void Dfs(int u, int fa) {
	siz[u] = 1;
	for(auto v : e[u]) {
		if(v == fa) {
			continue;
		}
		Dfs(v, u), siz[u] += siz[v];
		cnt[siz[v]]++, cnt[n - siz[v]]++;
	}
}
inline ll C(int n, int m) {
	if(n < m || m < 0) {
		return 0;
	}
	return fact[n] * invfact[m] % Mod * invfact[n - m] % Mod;
}
int main() {
	ig = QuickPow(g, Mod - 2);
	int i;
	n = Read();
	fact[0] = invfact[0] = 1;
	for(i = 1; i < N; i++) {
		fact[i] = fact[i - 1] * i % Mod;
		invfact[i] = QuickPow(fact[i], Mod - 2);
	}
	for(i = 1; i < n; i++) {
		int u = Read(), v = Read();
		e[u].emplace_back(v), e[v].emplace_back(u);
	}
	Dfs(1, 0);
	cnt[0] = 0;
	for(i = 0; i <= n; i++) {
		a[i] = 1ll * cnt[i] * fact[i] % Mod, b[i] = invfact[n - i];
	}
	l = 1;
	while((1 << l) <= n * 2) {
		l++;
	}
	for(i = 0; i < (1 << l); i++) {
		r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
	}
	NTT(a, 1), NTT(b, 1);
	for(i = 0; i < (1 << l); i++) {
		a[i] = (a[i] * b[i]) % Mod;
	}
	NTT(a, -1);
	ll tmp = QuickPow(1 << l, Mod - 2);
	for(i = n + 1; i <= n * 2; i++) {
		ll t = a[i] * tmp % Mod;
		Write((1ll * n * C(n, i - n) % Mod - invfact[i - n] * t % Mod + Mod) % Mod), putchar('\n');
	}
	return 0;
}