AGC004 题解
A - Divide a Cuboid
显然长方体必须被平行于某个面切开,否则不满足要求。
枚举被哪个面切开,设这个面是 \(a \times b\),不属于这个面的棱长为 \(c\),如果可以从正中间切开,即 \(c \bmod 2 = 0\) 时就从正中间切开,红蓝块个数差值为 \(0\)。否则,\(c \bmod 2 = 1\),从正中间偏移 \(0.5\) 格切开最优,红蓝块个数差值为 \(a \times b\)。
由于 \(a, b, c \ge 2\),所以没有边界情况,放心计算三种情况取最小值即可。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
ll Solve(ll a, ll b, ll c) {
return (a & 1) ? (b * c) : 0ll;
}
int main() {
ll a = Read(), b = Read(), c = Read();
Write(min(Solve(a, b, c), min(Solve(b, a, c), Solve(c, a, b))));
return 0;
}
B - Colorful Slimes
\(N\) 很小,考虑枚举操作二次数 \(k\),容易发现此时 \(i\) 号颜色的史莱姆可以由 \(j\) 号颜色的史莱姆变换而来,当且仅当 \((i - j + N) \bmod N \le k\),即操作二次数小于等于 \(k\)(若进行 \(p\) 次操作,那么可以在 \(k - p\) 次操作后购买史莱姆)。
因此只需从 \(0 \sim N - 1\) 枚举 \(k\),对所有数取向前 \(k\) 个数及其本身的最小值求和,再加上 \(k \cdot x\) 即可。
复杂度 \(O(N^2)\),当然貌似可以用三分降到 \(O(N \log N)\),但是我懒。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 2005;
int n;
ll a[N], b[N];
int main() {
int i, j;
ll x;
n = Read(), x = Read();
ll ans = LONG_LONG_MAX;
for(i = 1; i <= n; i++) {
a[i] = b[i] = Read();
}
for(i = 0; i < n; i++) {
ll res = 0;
for(j = 1; j <= n; j++) {
b[j] = min(b[j], a[(j - i + n - 1) % n + 1]);
res += b[j];
}
ans = min(ans, res + x * i);
}
Write(ans);
return 0;
}
C - AND Grid
注意到边界不会填充颜色这个条件。
我们设想:若有一个图形,使得无论后续填充哪个格子,这个图形总是连通的。
容易发现其充要条件为每一个格子都挨着一个图形的已被填充的方格。
记构造的第一个网格为 \(a\),第二个网格为 \(b\),可以构造如下图形:
- 填充 \(a\) 的第一列,与 \(b\) 的最后一列;
- \(a, b\) 交替填充每一行中除去第一个和最后一个剩下的方格。
如 \(H = 6, W = 5\) 时,我们有如下构造:
####.
#....
####.
#....
####.
#....
....#
.####
....#
.####
....#
.####
当然这样构造也是合理的(代码中采用本种构造):
#....
####.
#....
####.
#....
####.
.####
....#
.####
....#
.####
....#
再在原有网格中的所有填充的位置,将 \(a, b\) 中的对应位置填充。
如样例 \(1\):
#....
####.
#....
####.
#....
.####
.#.##
.####
.#.##
.####
由于在“在原有网格中的所有填充的位置,将 \(a, b\) 中的对应位置填充”这一步之前,\(a, b\) 互不重叠,而最后 \(a, b\) 重叠的位置一定是在原有网格中的填充的位置(因为只影响了这些方格),同时我们发现每个被填充的位置一定被重叠了(因为 \(a, b\) 中这个方格一定被填充),因此这种构造合法。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 505;
int n, m;
string s[N], a[N], b[N];
int main() {
int i, j;
cin >> n >> m;
for(i = 0; i < n; i++) {
cin >> s[i];
a[i] = b[i] = s[i];
}
for(i = 0; i < n; i++) {
a[i][0] = b[i][m - 1] = '#';
if(i & 1) {
for(j = 1; j < m - 1; j++) {
a[i][j] = '#';
}
}
else {
for(j = 1; j < m - 1; j++) {
b[i][j] = '#';
}
}
}
for(i = 0; i < n; i++) {
cout << a[i] << endl;
}
cout << endl;
for(i = 0; i < n; i++) {
cout << b[i] << endl;
}
return 0;
}
D - Teleporter
首先,\(1\) 号结点的传送门一定指向它本身,若不是这样,则令为 \(u\) 满足经过 \(K\) 次传送到 \(1\) 号结点,\(u\) 指向 \(v\),那么 \(v\) 经过 \(K - 1\) 次传送到 \(1\) 号结点,下一次传送一定不是 \(1\) 号结点,不符题意。
这样的话,你会发现除去 \(1\) 号结点的自环,所有结点构成了一棵以 \(1\) 号结点为根的内向树,所以我们的策略一定是将某些点指向 \(1\) 号结点,显然这样做比指向其它结点更优。
考虑在树上贪心的选点,考虑树的结构,自深到浅考虑,每次必须要改变指向结点时(若不更改,则子树内有结点到 \(1\) 的距离大于 \(K\)),就贪心的更改,感性理解还是挺对的。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, k, a[N], dep[N], ans = 0;
vector<int> e[N];
void Dfs(int u, int cdep) {
dep[u] = cdep;
for(auto v : e[u]) {
Dfs(v, cdep + 1), dep[u] = max(dep[v], dep[u]);
}
if(dep[u] - cdep == k - 1 && a[u] != 1) {
dep[u] = cdep - 1, ans++;
}
}
int main() {
int i;
n = Read(), k = Read();
for(i = 1; i <= n; i++) {
a[i] = Read();
if(i > 1) {
e[a[i]].emplace_back(i);
}
}
ans = (a[1] != 1), a[1] = 1;
Dfs(1, 1);
Write(ans);
return 0;
}
E - Salvage Robots
考虑我们定下能够被其拯救的机器人相对于出口的范围,然后只去尝试拯救这些范围之内的机器人。
设出口坐标为 \((ex, ey)\),我们用四个数 \(u, d, l, r\),表示只去尝试拯救横坐标在 \([ex - u, ex + d]\) 范围内,纵坐标在 \([ey - l, ey + r]\) 范围内的机器人。
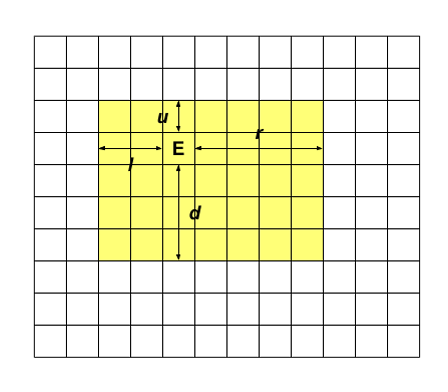
如官方题解中的图所示,此时:
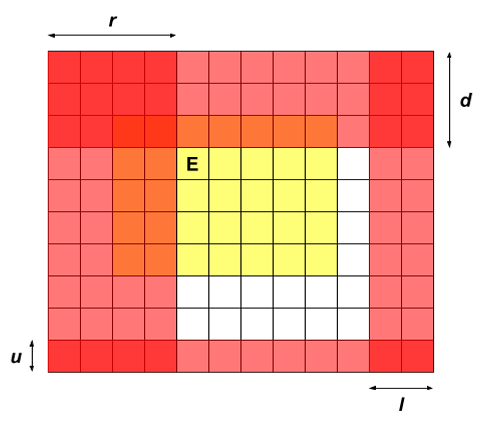
只被红色覆盖的格子中的机器人已经无法被拯救了,不用考虑转移。
考虑转移,我们用 \(f_{u, d, l, r}\) 表示只去尝试拯救横坐标在 \([ex - u, ex + d]\) 范围内,纵坐标在 \([ey - l, ey + r]\) 范围内的机器人(这样红色格子的范围是固定的),最多能拯救多少个。
我们可以从 \(f_{u, d, l, r}\) 转移到 \(f_{u + 1, d, l, r}\)、\(f_{u, d + 1, l, r}\)、\(f_{u, d, l + 1, r}\) 及 \(f_{u, d, l, r + 1}\),其中,从 \(f_{u, d, l, r}\) 转移到 \(f_{u + 1, d, l, r}\),表示我们先去拯救横坐标在 \([ex - u, ex + d]\) 范围内,纵坐标在 \([ey - l, ey + r]\) 范围内的机器人,再去拯救多出来的一行机器人,其它三种转移类似。
显然我们只能拯救白色格子里的机器人,如下图,当我们将黄色格子向下及向右推进一格时,分别能拯救紫色和绿色格子里的机器人。
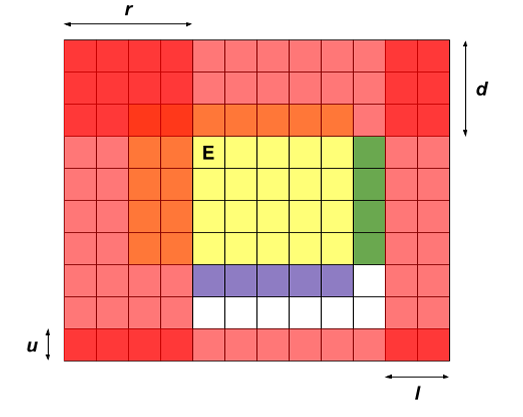
由图我们能直观地推出 \((x, y)\) 不在红色格子里的条件:
- \(x \in [d + 1, n - u]\);
- \(y \in [r + 1, m - l]\)。
当我们往上、下推进时,纵坐标的范围为 \([ey - l, ey + r]\),同理,当我们往左、右推进时,横坐标的范围为 \([ex - u, ex + d]\)。
综合以上两条,即可得到新增白色格子的数目。
DP 即可,复杂度 \(O(N^2 M^2)\),要用 short 压一下空间。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 105;
int n, m;
int sum[N][N];
short f[N][N][N][N];
string s[N];
int Sum(int a, int b, int c, int d) {
return (a > c || b > d) ? 0 : (sum[c][d] - sum[a - 1][d] - sum[c][b - 1] + sum[a - 1][b - 1]);
}
int main() {
int i, j, k, l;
cin >> n >> m;
for(i = 1; i <= n; i++) {
cin >> s[i];
s[i] = "." + s[i];
}
bool suc = false;
int ex = 0, ey = 0;
for(i = 1; i <= n; i++) {
for(j = 1; j <= m; j++) {
if(s[i][j] == 'E') {
ex = i, ey = j, suc = true;
break;
}
}
if(suc) {
break;
}
}
for(i = 1; i <= n; i++) {
for(j = 1; j <= m; j++) {
sum[i][j] = (s[i][j] == 'o');
}
}
for(i = 1; i <= n; i++) {
for(j = 1; j <= m; j++) {
sum[i][j] += sum[i - 1][j];
}
}
for(i = 1; i <= n; i++) {
for(j = 1; j <= m; j++) {
sum[i][j] += sum[i][j - 1];
}
}
// U : x > j
// D : n - x + 1 > i
// L : y > l
// R : m - y + 1 > k
// x \in [j + 1, n - i]
// y \in [l + 1, m - k]
int ans = 0;
for(i = 0; i < ex; i++) {
for(j = 0; j <= n - ex; j++) {
for(k = 0; k < ey; k++) {
for(l = 0; l <= m - ey; l++) {
if(ex - i - 1 >= j + 1) {
f[i + 1][j][k][l] = max(int(f[i + 1][j][k][l]), f[i][j][k][l] + Sum(ex - i - 1, max(l + 1, ey - k), ex - i - 1, min(m - k, ey + l)));
}
if(ex + j + 1 <= n - i) {
f[i][j + 1][k][l] = max(int(f[i][j + 1][k][l]), f[i][j][k][l] + Sum(ex + j + 1, max(l + 1, ey - k), ex + j + 1, min(m - k, ey + l)));
}
if(ey - k - 1 >= l + 1) {
f[i][j][k + 1][l] = max(int(f[i][j][k + 1][l]), f[i][j][k][l] + Sum(max(j + 1, ex - i), ey - k - 1, min(n - i, ex + j), ey - k - 1));
}
if(ey + l + 1 <= m - k) {
f[i][j][k][l + 1] = max(int(f[i][j][k][l + 1]), f[i][j][k][l] + Sum(max(j + 1, ex - i), ey + l + 1, min(n - i, ex + j), ey + l + 1));
}
ans = max(ans, int(f[i][j][k][l]));
}
}
}
}
Write(ans);
return 0;
}
F - Namori
感谢 @Oier_szc 的建议。
以下将把某个点的颜色变为相反的颜色,称之为把颜色取反。
F.1 树
先看树的部分分,直接做不那么直观,因为树是二分图,可以考虑把树黑白染色,还是看官解里的图:
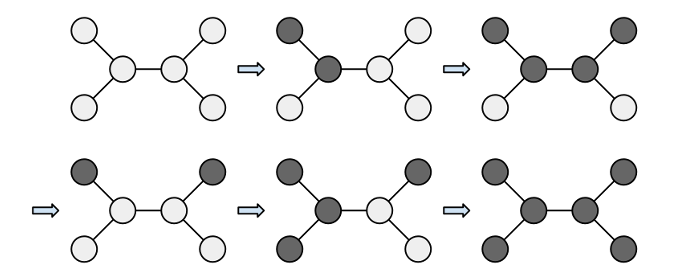
这是转化之前样例一的染色方案。
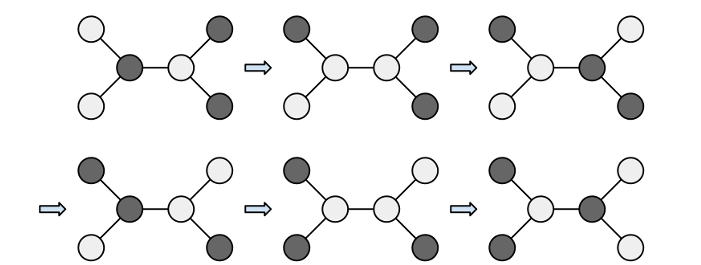
这是转化之后样例一的染色方案。简单来说,就是按二分图的染色方式,将二分图被染成黑点的点的初始颜色取反,变成黑色,这样目标状态中,二分图被染成黑点的点的颜色也应被取反,变成白色。此时,限制条件由“两个点颜色相同”,变成了“两个点颜色不同”,由于条件的转换,我们可以把“将两点颜色取反”,变为“交换两点的颜色”。
梳理一下转化后的题意:
- 给定一个被二分图染色后的树,每次可以交换一条边两个不同颜色的点的颜色,使得最终的树是原树中所有点的颜色被取反后形成的树,求最小操作次数。
现在我们就可以直接得到,一棵树无解的充要条件是:将这棵树二分图黑白染色后,黑白点个数不相等。
进一步的,考虑对于一棵子树,假设其白点数量为 \(a\),黑点数量为 \(b\),那么,因为其目标状态为,其白点数量为 \(b\),黑点数量为 \(a\),且一次操作最多可以是黑点与白点的差加 \(2\) 或减 \(2\),因此,发生在这棵子树的根连向其父亲的边上的交换操作至少为 \(|a - b|\) 次。
因此答案的下界为一棵树所有子树的黑白点数量之差,我们来大致证明一下操作数能达到这个下界。
我们考虑对于一条边 \(e = (u, v)\),如下图所示:
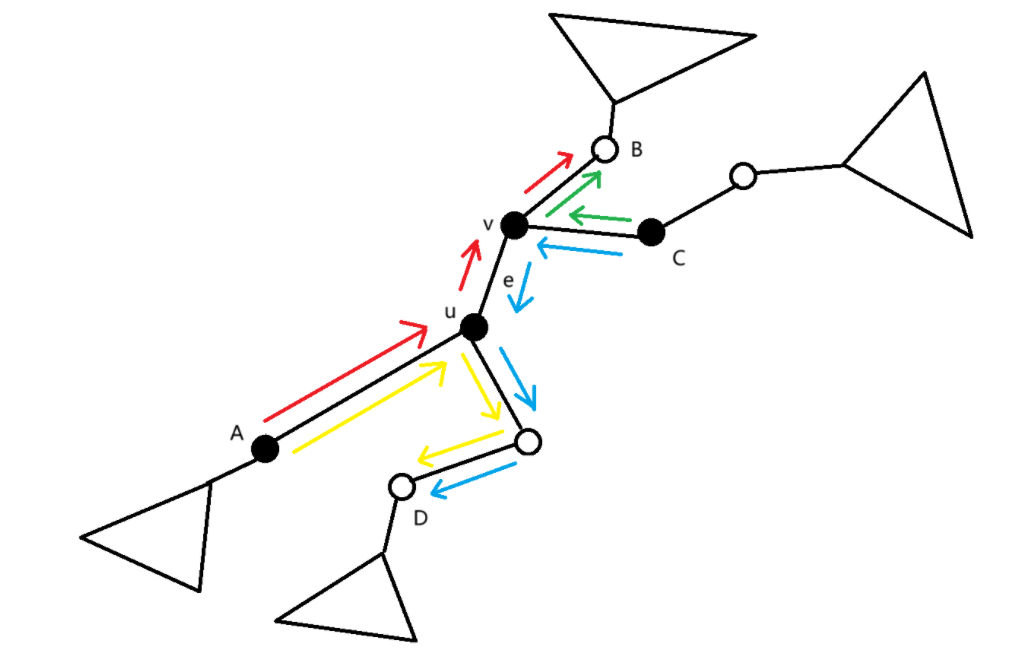
假设 \(u\) 点一侧的子树与 \(v\) 点一侧的子树,均满足黑白点数量已经与目标的黑白点数量相同,我们称此时边 \(e\) 处于平衡状态。
如果黑色的 \(A\) 点要按红色路径转移到白色的 \(B\) 点,因为这样打破了边 \(e\) 的平衡状态,必然存在黑色的 \(C\) 点要按蓝色路径转移到白色的 \(D\) 点。
那么这样显然劣于黑色的 \(A\) 点按黄色路径转移到白色的 \(D\) 点,黑色的 \(C\) 点按绿色路径转移到白色的 \(B\) 点。
所以,我们得到结论,若 \(e\) 处于平衡状态,那么可以直接断开 \(e\),将原树划分成两颗子树,递归的解决问题,因此,这种处于平衡状态的边对答案没有影响。
再考虑不处于平衡状态的边,我们发现,对于一个边 \(e = (u, v)\) 上的交换操作,假设 \(u\) 侧缺黑点,\(v\) 侧多出了一些黑点。那么只有将黑点从 \(v\) 点转移到 \(u\) 才是不劣的,因此我们可以尝试对每一条边定向,表示黑点怎样转移才是优的,如下图所示(用双向边表示处于平衡状态的边)。
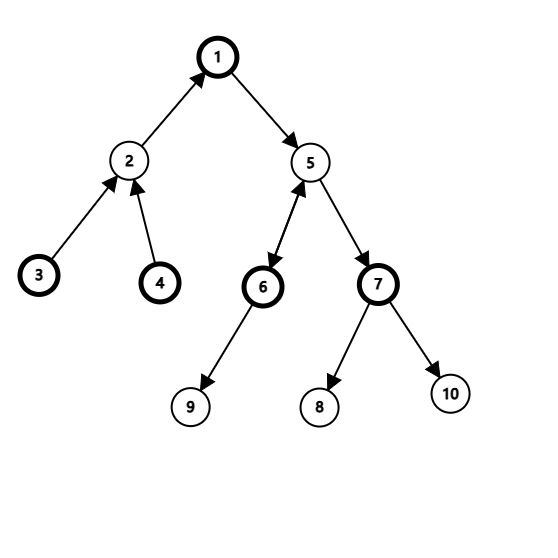
我们若想达到操作次数的下界,那么一定是将黑点向箭头方向移动,直到所有边都是平衡状态。
但是,假设出现了以下两种情况(\(B, C, D, ...\) 处表示的是一棵子树,而不是一个结点):
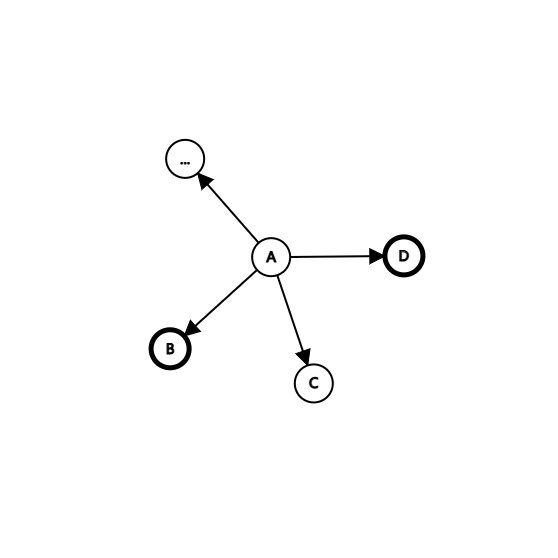
\(A\) 处为白点,且以 \(A\) 点为端点的边都不指向 \(A\) 点,那么 \(A\) 处的黑点就转移不出去了。
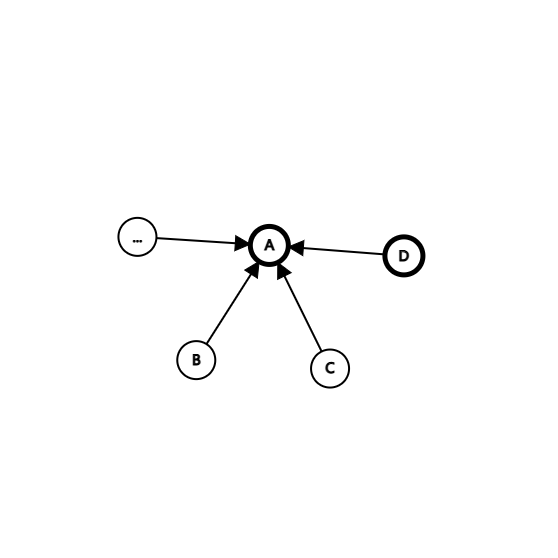
\(A\) 处为黑点,且以 \(A\) 点为端点的边都指向 \(A\) 点,那么从 \(B, C, D, ...\) 处的黑点就转移不到其他地方了(相当于 \(A\) 处的黑点把路“堵住”了)。
这样看起来都达不到下界,但是我们可以证明两种情况均是不存在的。
证明:第一种情况中 \(B, C, D, ...\) 处都缺黑点,即黑点个数小于白点个数,而 \(A\) 点为白点,如果它的目标状态是黑点,那它也可以视为缺黑点,反之它不缺点,所以整棵树缺黑点,即黑点个数小于白点个数,无解,第二种情况同理。
通过以上结论,我们可以发现,边被定向后,整棵树大致构成一个 DAG,且 DAG 的若干个源点处一定是黑点,汇点处一定是白点,所以黑点只要沿 DAG 的方向流动,操作数一定能达到下界。
因此,我们大致证明了,总存在一种合法的方案使得答案能达到下界。
对每条边进行计数即可,具体实现中,可以将黑点权值设为 \(1\),白点权值设为 \(-1\),再统计每个子树权值和的绝对值之和。
F.2 基环树且环为偶环
注意到图仍是二分图。所以这种情况下无解的情况与树相同。
通过上面的结论,我们也可以把所有不在环上的边定向,同时,我们对环上的点赋一个权值 \(val\),表示将黑点权值设为 \(1\),白点权值设为 \(-1\),该子树所有结点权值和。
如果对树的做法理解透彻,你会发现每个子树的权值和,其实是由子树的根结点连向其父亲结点的边的有向权值。
这里“有向”的意思是,由子树的根结点的父亲结点连向它本身的边的有向权值,是由子树的根结点连向其父亲结点的边的有向权值的相反数,具体的,我们可以定义,由 \(u\) 连向 \(v\) 的有向权值 \(val\),表示必须要由 \(u\) 向 \(v\) 输送 \(val\) 个黑点(\(val > 0\)),或是必须要由 \(v\) 向 \(u\) 输送 \(-val\) 个黑点(\(val < 0\)),才能使这条边达到平衡状态。
这样,我们可以假设,环上的点依次是 \(p_1, p_2, \dots, p_k\),\(p_i\) 的权值为 \(a_i\),由 \(p_i\) 连向 \(p_{i \bmod k + 1}\) 的边的有向权值为 \(y_i\)。
这样,我们可以得到:
令 \(x_i = -y_{(i - 2 + k) \bmod k + 1}\),得到:
也即:
显然这个方程没有唯一解(例如,可以令 \(x_i' = x_i + t\) 得到一组新解)。
我们的目标是最小化 \(\sum_{i = 1}^k |x_i|\)。注意到:
因此:
问题转化为,在数轴上标出 \(0\),\(a_1\),\(a_1 + a_2\),\(\sum_{i = 0}^{k - 1} a_i\) 这 \(k\) 个点,我们现在要找到一个点 \(x_1\),使得 \(x_1\) 到其它 \(k\) 个点的距离和最短。这是一个经典问题,当 \(x_1\) 取所有数的中位数时,总距离最小。
因此在求出环外各边权值的绝对值之和后,计算环上各边的权值,按上述步骤求处环上边的最小权值和即可。
F.3 基环树且环为奇环
对于奇环的情况,考虑断掉环上的一条边后,整个图变成了一棵树,我们仍然对这棵树黑白染色,则该断掉的边的两个端点同色。
因此,这一条边的作用即为,当该边的两个端点颜色相同时,将两个端点的颜色取反。
这样,我们可以不断生成 \(2\) 个黑点或白点,这种情况下,黑点与白点的差值只会加 \(2\) 或减 \(2\),同时,我们的目标是让原图中所有点的颜色被取反。
所以,我们得到了这种情况下,无解的充要条件是:在断掉环上的一条边并对这棵树黑白染色后,黑白点个数奇偶性相同,当然,这与“\(N\) 为偶数”这一条件是等价的。
由树的情况,我们可以证明,这一条边只能不断生成黑点或不断生成白点(具体的,考虑这种情况是答案的下界,可以先把答案加上生成次数,再在这个结点上叠若干个黑点或白点,发现叠黑点的情况可以使树中的两个结论都成立)。
因此令 \(x\) 为黑点个数减白点个数,则整棵树的权值和为 \(x\),先将答案加上 \(\frac{|x|}{2}\),然后叠黑点或白点,即将两个点的权值减去 \(\frac{x}{2}\)(注意整棵基环树的权值和为 \(0\) 时,我们才能恰好补齐黑点或白点并把边割掉转化为树,原因在于,注意到我们每次加黑点或者白点,不仅加上了两个被生成的点的权值,还减去了两个被替换的异色点的权值,而在原树中我们并没有减去这些被替换点的贡献,这与被生成的点的权值恰好相抵消),再跑树的做法即可。
(想不到更好的讲法,若有请告知 QwQ)
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n;
bool col[N];
vector<int> e[N];
ll ans = 0, val[N];
void Dfs(int u, int fa, bool pcol) {
col[u] = !pcol;
for(auto v : e[u]) {
if(v == fa) {
continue;
}
Dfs(v, u, col[u]);
}
}
ll Dfs2(int u, int fa) {
ll res = val[u];
for(auto v : e[u]) {
if(v == fa) {
continue;
}
res += Dfs2(v, u);
}
ans += abs(res);
return res;
}
vector<int> st;
bool vis[N], c[N], suc = false;
int cnt = 0;
vector<int> cir;
void Dfs3(int u, int fa) {
st.emplace_back(u);
vis[u] = true;
for(auto v : e[u]) {
if(v == fa) {
continue;
}
if(vis[v]) {
if(!suc) {
suc = true;
bool b = false;
for(auto x : st) {
if(x == v) {
b = true;
}
c[x] = b, cnt += b;
if(b) {
cir.emplace_back(x);
}
}
}
continue;
}
Dfs3(v, u);
}
st.pop_back();
}
void Dfs4(int u, bool pcol) {
col[u] = !pcol, vis[u] = true;
for(auto v : e[u]) {
if(vis[v]) {
continue;
}
Dfs4(v, col[u]);
}
}
ll Dfs5(int u, int fa) {
ll res = col[u] ? 1 : -1;
for(auto v : e[u]) {
if(v == fa || c[v]) {
continue;
}
res += Dfs5(v, u);
}
ans += abs(res);
return res;
}
int main() {
int i, m;
n = Read(), m = Read();
for(i = 1; i <= m; i++) {
int u = Read(), v = Read();
e[u].emplace_back(v), e[v].emplace_back(u);
}
if(m == n - 1) {
Dfs(1, 0, false);
int sum = 0, i;
for(i = 1; i <= n; i++) {
sum += col[i];
val[i] = col[i] ? 1 : -1;
}
if(sum * 2 != n) {
printf("-1");
return 0;
}
Dfs2(1, 0);
Write(ans);
return 0;
}
Dfs3(1, 0);
if(cnt & 1) {
int u, v;
for(i = 1; i <= n; i++) {
if(c[i]) {
u = i;
break;
}
}
for(auto x : e[u]) {
if(c[x]) {
v = x;
break;
}
}
for(i = 0; i < e[u].size(); i++) {
if(e[u][i] == v) {
break;
}
}
e[u].erase(e[u].begin() + i);
for(i = 0; i < e[v].size(); i++) {
if(e[v][i] == u) {
break;
}
}
e[v].erase(e[v].begin() + i);
Dfs(1, 0, false);
int sum = 0, i;
for(i = 1; i <= n; i++) {
sum += col[i];
val[i] = col[i] ? 1 : -1;
}
if(n & 1) {
printf("-1");
return 0;
}
ll x = n / 2 - sum;
val[u] += x, val[v] += x;
Dfs2(1, 0);
Write(ans + abs(x));
}
else {
memset(vis, 0, sizeof(vis));
Dfs4(1, false);
int sum = 0;
for(i = 1; i <= n; i++) {
sum += col[i];
val[i] = col[i] ? 1 : -1;
}
if(sum * 2 != n) {
printf("-1");
return 0;
}
memset(vis, 0, sizeof(vis));
vector<ll> vec;
for(auto v : cir) {
ll x = Dfs5(v, 0);
vec.emplace_back(x), ans -= abs(x);
}
for(i = 1; i < vec.size(); i++) { // \sum val_i = 0
vec[i] += vec[i - 1];
}
sort(vec.begin(), vec.end());
ll x = vec[vec.size() / 2];
for(auto v : vec) {
ans += abs(x - v);
}
Write(ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号