AGC002 题解
A - Range Product
分情况讨论:
- \(a \le 0 \le b\) 时,乘积一定为 \(0\);
- 否则:
- \(0 < a \le b\) 时,乘积一定为正;
- 否则,负数的个数有 \(b - a + 1\) 个,判断这个数是否为奇数,若是,乘积为负,否则为正。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
int main() {
int a = Read(), b = Read();
if(a <= 0 && b >= 0) {
printf("Zero\n");
}
else {
bool p = false;
if(a > 0 && b > 0) {
p = true;
}
else {
p = (b - a) & 1;
}
if(p) {
printf("Positive\n");
}
else {
printf("Negative\n");
}
}
return 0;
}
B - Box and Ball
考虑对于每个操作,动态记录里面是否有红球。
如果将盒子 \(x\) 中的一个球放到盒子 \(y\) 中:
- 若盒子 \(x\) 中可能有红球,那么盒子 \(y\) 中也可能有红球;
- 假设盒子 \(x\) 中已经没有球了,那么盒子 \(x\) 也不可能有红球。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, cnt[N];
bool a[N];
int main() {
int i, m;
n = Read(), m = Read();
for(i = 1; i <= n; i++) {
cnt[i] = 1;
}
a[1] = true;
while(m--) {
int u = Read(), v = Read();
cnt[v]++, cnt[u]--, a[v] |= a[u];
if(!cnt[u]) {
a[u] = false;
}
}
int ans = 0;
for(i = 1; i <= n; i++) {
ans += a[i];
}
Write(ans);
return 0;
}
C - Knot Puzzle
对于一段完整的绳子,剪去最左边或最右边的小绳子比不这么做是不优的。证明可以考虑,存在至少一种剪法,使得前者留下的较长的绳子比后者留下的较短的且需要被再次剪开的绳子长。
倒着考虑,假设最后一步的绳长不小于 \(L\),则前面所有步的绳长均不小于 \(L\),留下总长最长的两段连续的小绳子最后剪即可。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n;
ll a[N], k;
int main() {
int i, j = 0;
n = Read(), k = Read();
for(i = 1; i <= n; i++) {
a[i] = Read();
if(a[i] + a[i - 1] > a[j] + a[j - 1]) {
j = i;
}
}
if(a[j] + a[j - 1] < k) {
printf("Impossible\n");
return 0;
}
printf("Possible\n");
for(i = 1; i < j - 1; i++) {
Write(i), putchar('\n');
}
for(i = n - 1; i >= j; i--) {
Write(i), putchar('\n');
}
Write(j - 1), putchar('\n');
return 0;
}
D - Stamp Rally
参考 @_SeeleVollerei_ 的题解
显然答案具有单调性,因此可以二分答案,每次总是加上一个前缀的边,然后用并查集判断集合大小是否不小于 \(z\)。
这样的复杂度是 \(O(QM \log M \log N)\) 的。
显然不可承受,考虑如何把 \(M\) 给去掉。
注意到,如果我们采用按秩合并的并查集,我们可以通过记录时间戳来还原在某一时刻的并查集,因此我们仍然可以愉快的二分答案,复杂度 \(O(Q \log M \log N)\)。
具体实现时,可以对每条边(就是并查集中每个结点到它父亲的连边)记录时间戳,同时对每个结点的子树大小记录历史版本及其第一次被更新到该版本的时间戳。二分 Check 时,两个点分别暴力往上跳直到不能跳为止,若两个点不同(说明两个点在该时刻不连通),则将两个点的子树大小相加得到最大的可到点数,若两个点相同,那个点的子树大小即为最大的可达点数。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, m;
struct DSU {
pair<int, int> fa[N];
vector<pair<int, int> > siz[N];
void Init(int n) {
int i;
for(i = 1; i <= n; i++) {
fa[i] = make_pair(0, i), siz[i].emplace_back(0, 1);
}
}
int Find_Root(int t, int u) {
return (fa[u].second == u || fa[u].first > t) ? u : Find_Root(t, fa[u].second);
}
void Join(int t, int u, int v) {
int ru = Find_Root(N, u), rv = Find_Root(N, v);
if(ru == rv) {
return ;
}
int su = siz[ru].back().second, sv = siz[rv].back().second;
if(su > sv) {
swap(ru, rv);
}
siz[rv].emplace_back(t, su + sv);
fa[ru].second = rv, fa[ru].first = t;
}
int Get_Siz(int t, int u) {
int l = 0, r = siz[u].size() - 1, mid, res = 0;
while(l <= r) {
mid = (l + r) >> 1;
if(siz[u][mid].first <= t) {
res = mid, l = mid + 1;
}
else {
r = mid - 1;
}
}
return siz[u][res].second;
}
bool Check(int t, int u, int v, int w) {
int ru = Find_Root(t, u), rv = Find_Root(t, v);
if(ru != rv) {
return Get_Siz(t, ru) + Get_Siz(t, rv) >= w;
}
return Get_Siz(t, ru) >= w;
}
int Query(int u, int v, int w) {
int l = 1, r = m, mid, res = m;
while(l <= r) {
mid = (l + r) >> 1;
if(Check(mid, u, v, w)) {
res = mid, r = mid - 1;
}
else {
l = mid + 1;
}
}
return res;
}
}dsu;
int main() {
int i, q;
n = Read(), m = Read();
dsu.Init(n);
for(i = 1; i <= m; i++) {
int u = Read(), v = Read();
dsu.Join(i, u, v);
}
q = Read();
while(q--) {
int u = Read(), v = Read(), w = Read();
Write(dsu.Query(u, v, w)), putchar('\n');
}
return 0;
}
E - Candy Piles
考虑将 \(a\) 数组从小到大排序,构造一个 \(N \times a_N\) 的黑白网格图,记第 \(i\) 行第 \(j\) 列的网格为 \((i, j)\),则 \((i, j)\) 的颜色为黑当且仅当 \(j \le a_i\)。
则问题转化为,每次可以删去第一行或最后一列,谁先将黑格子删光谁输。
每次留下的一定是在某个网格 \((i, j)\) 与 \((1, a_N)\) 构成的矩形内的所有格子,考虑将 \((i, j)\) 作为一个状态。
首先若 \((i, j)\) 与 \((1, a_N)\) 构成的矩形内的所有格子均为白色,则这个格子为必胜态,每个格子的后继状态又最多只有 \((i, j + 1)\) 与 \((i - 1, j)\) 两种。
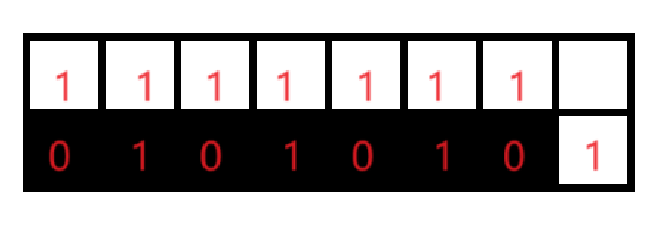
如 \(N = 6, \{a_i\} = \{1, 1, 3, 4, 7, 7\}\) 时图长这样,格子里的红色数字表示 \(f(i, j)\):

因此我们可以得到一个 \(O(N \times \max\{a_i\})\) 的 DP 做法。
考虑优化,注意到:
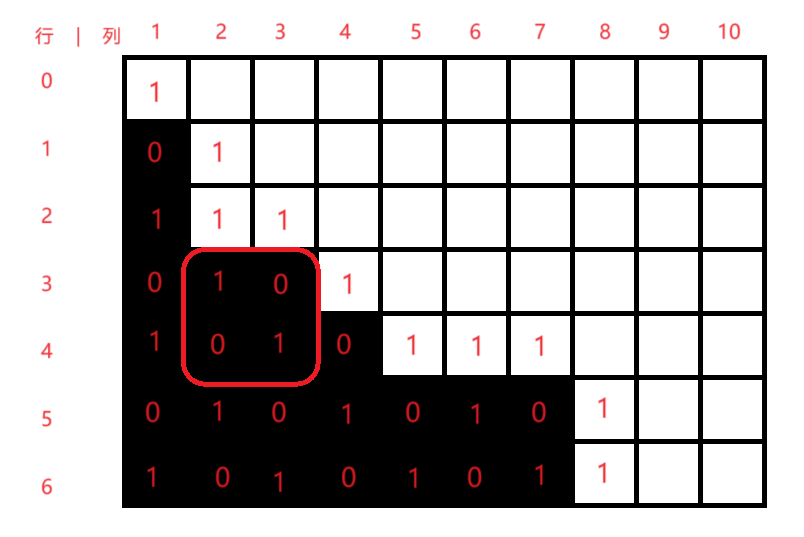
- 记 \((i, j)\) 的状态为 \(f(i, j)\)(表示 \((i, j)\) 是否为必胜态),若 \((i, j)\) 为黑格,\((i - 1, j + 1)\) 也是黑格,则 \(f(i, j) = f(i - 1, j + 1)\)。
证明:如果 \(f(i - 1, j + 1) = 0\),那么根据定义,\(f(i, j + 1) = f(i - 1, j) = 1\),则 \(f(i, j) = 0 = f(i - 1, j + 1)\),如图中被红框框住的部分。
如果 \(f(i - 1, j + 1) = 1\),假设 \(f(i, j) = 0\),则根据定义可得 \(f(i - 1, j) = f(i, j + 1) = 1\),此时:
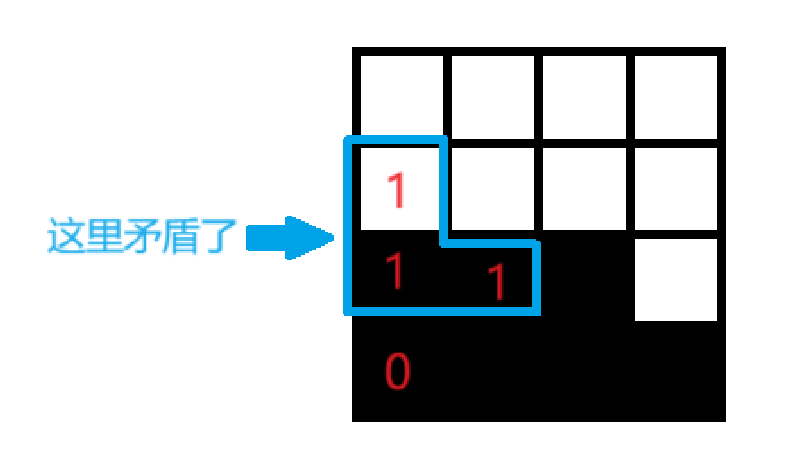
- 若 \((i, j + 2)\) 或 \((i - 2, j + 2)\) 是边界,那么它的 \(f\) 值为 \(1\),此时边界与 \((i, j)\) 中间夹着的格子,\((i - 1, j + 1)\),及边界的 \(f\) 值都为 \(1\),不符合定义,如下图:
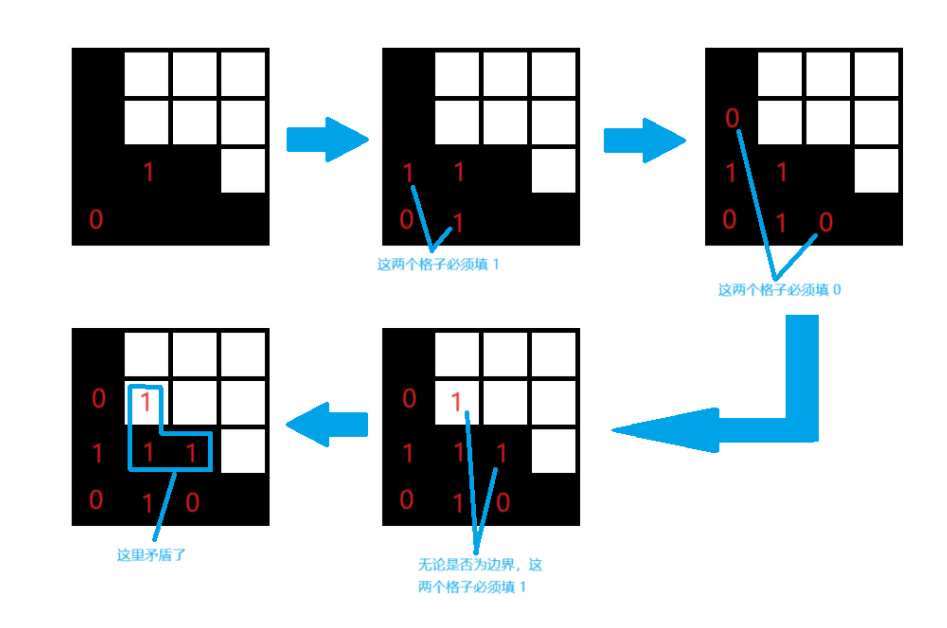
- 若 \((i, j + 2)\) 和 \((i - 2, j + 2)\) 均不是边界,那么根据下图可以推出矛盾:
综上,命题得证。由于网格图的行数只有 \(N\),所以可以愉快地计算对角线上最靠右上角的网格进行计算。
注意到:
因此可以算出最靠右上角的网格到右边界与上边界的距离,根据奇偶性进行判断。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 100005;
int n, a[N];
int main() {
int i, x = 0, y = 0;
n = Read();
for(i = 1; i <= n; i++) {
a[i] = Read();
}
sort(a + 1, a + n + 1);
for(i = n; i; i--) {
if(a[i] < n - i + 1) {
break;
}
}
i++;
while(x < i) {
if(a[i - x] < n - i + 1) {
break;
}
x++;
}
y = a[i] - n + i;
if((x & 1) && (y & 1)) {
printf("Second\n");
}
else {
printf("First\n");
}
return 0;
}
F - Leftmost Ball
考虑 DP,以每个白球为分界线设计状态。
设 \(f_{i, j}\) 表示已经放了 \(i\) 个白球和 \(j\) 种其他颜色的所有球的方案数,需满足 \(i \ge j\)。
考虑转移:
- 当前第一个空位放白球时(从 \(f_{i - 1, j}\) 转移过来),这个白球可能是某一种颜色的第一个球染成的,而这个颜色还未确定,因此这个白球一定合法,贡献系数为 \(1\)。
- 当前第一个空位放其他颜色的球时(从 \(f_{i, j - 1}\) 转移过来),首先我们要决定颜色,一共有 \(N - j + 1\) 种,我们要同时放置同一颜色的剩下所有 \(K - 2\) 个球,而除去第一个空位还剩 \(N \times K - i - (j - 1) \times (K - 1) - 1\) 个空位(总空位数,减去白球数量,减去有颜色的球的数量,再减去第一个空位),因此放置方案数为 \(\dbinom{N \times K - i - (j - 1) \times (K - 1) - 1}{K - 2}\),将其与颜色数相乘即可。
因此转移式为:
边界为 \(f_{i, 0} = 1\),特判 \(K = 1\) 的情况。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll Read() {
int sig = 1;
ll num = 0;
char c = getchar();
while(!isdigit(c)) {
if(c == '-') {
sig = -1;
}
c = getchar();
}
while(isdigit(c)) {
num = (num << 3) + (num << 1) + (c ^ 48);
c = getchar();
}
return num * sig;
}
void Write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x >= 10) {
Write(x / 10);
}
putchar((x % 10) ^ 48);
}
const int N = 2005;
const ll Mod = 1e9 + 7;
int n, k;
ll f[N][N], fact[N * N], invfact[N * N], inv[N * N];
void Init(int n) {
int i;
inv[1] = 1;
for(i = 2; i <= n; i++) {
inv[i] = Mod - Mod / i * inv[Mod % i] % Mod;
}
fact[0] = invfact[0] = 1;
for(i = 1; i <= n; i++) {
fact[i] = fact[i - 1] * i % Mod;
invfact[i] = invfact[i - 1] * inv[i] % Mod;
}
}
ll C(ll n, ll m) {
if(n < m || n < 0) {
return 0;
}
return fact[n] * invfact[m] % Mod * invfact[n - m] % Mod;
}
int main() {
Init(N * N - 1);
n = Read(), k = Read();
if(k == 1) {
printf("1");
return 0;
}
int i, j;
for(i = 1; i <= n; i++) {
f[i][0] = 1;
for(j = 1; j <= i; j++) {
f[i][j] = (f[i - 1][j] + f[i][j - 1] * (n - j + 1) % Mod * C(n * k - i - (j - 1) * (k - 1) - 1, k - 2) % Mod) % Mod;
}
}
Write(f[n][n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号