基于DCT变换图像去噪算法的终极优化(1920*1080灰度图单核约22ms)
相关文章:
优化IPOL网站中基于DCT(离散余弦变换)的图像去噪算法(附源代码)。
SSE图像算法优化系列二十一:基于DCT变换图像去噪算法的进一步优化(100W像素30ms)。
这个算法2015年优化过一版,2018年又优化过一版,2016年初又来回访一下,感觉还有优化空间,继续又折腾了将近一周,速度又有进一步的提升,下面是这个三个版本在同一台电脑上的速度比较:

对于小图,其实2026版和2018年速度差异不是很大,到了大图,新版约有25%左右的提升。
那么2026版优化的渠道主要有两处,第一个还是内部DCT变换本身的优化,以8*8的DCT为例,2015版DCT1D的代码如下所示:
inline void IM_DCT1D_8x1_GT_C(float *In, float *Out) { const float mx00 = In[0] + In[7]; const float mx01 = In[1] + In[6]; const float mx02 = In[2] + In[5]; const float mx03 = In[3] + In[4]; const float mx04 = In[0] - In[7]; const float mx05 = In[1] - In[6]; const float mx06 = In[2] - In[5]; const float mx07 = In[3] - In[4]; const float mx08 = mx00 + mx03; const float mx09 = mx01 + mx02; const float mx0a = mx00 - mx03; const float mx0b = mx01 - mx02; const float mx0c = 1.38703984532215f * mx04 + 0.275899379282943f * mx07; const float mx0d = 1.17587560241936f * mx05 + 0.785694958387102f * mx06; const float mx0e = -0.785694958387102f * mx05 + 1.17587560241936f * mx06; const float mx0f = 0.275899379282943f * mx04 - 1.38703984532215f * mx07; const float mx10 = 0.353553390593274f * (mx0c - mx0d); const float mx11 = 0.353553390593274f * (mx0e - mx0f); Out[0] = 0.353553390593274f * (mx08 + mx09); Out[1] = 0.353553390593274f * (mx0c + mx0d); Out[2] = 0.461939766255643f * mx0a + 0.191341716182545f * mx0b; Out[3] = 0.707106781186547f * (mx10 - mx11); Out[4] = 0.353553390593274f * (mx08 - mx09); Out[5] = 0.707106781186547f * (mx10 + mx11); Out[6] = 0.191341716182545f * mx0a - 0.461939766255643f * mx0b; Out[7] = 0.353553390593274f * (mx0e + mx0f); }
可以看到Out[0]到Out[7]这个8个数据前面都还有很多系数,共有26次加法及22次乘法,实际上可以把他们和前面的系数融合到一起,修改后数据如下所示:
inline void IM_DCT1D_1x8_C(float* In, float* Out) { float V00 = In[0] + In[7]; float V01 = In[0] - In[7]; float V02 = In[1] + In[6]; float V03 = In[1] - In[6]; float V04 = In[2] + In[5]; float V05 = In[2] - In[5]; float V06 = In[3] + In[4]; float V07 = In[3] - In[4]; float V08 = 0.353553390593274f * (V00 + V06); float V09 = 0.353553390593274f * (V02 + V04); float V10 = V00 - V06; float V11 = V02 - V04; float V12 = 0.490392640201616f * V01 + 0.097545161008064f * V07; float V13 = 0.415734806151273f * V03 + 0.277785116509801f * V05; float V14 = 0.415734806151273f * V05 - 0.277785116509801f * V03; float V15 = 0.097545161008064f * V01 - 0.490392640201616f * V07; float V16 = 0.707106781186547f * (V12 - V13); float V17 = 0.707106781186547f * (V14 - V15); Out[0] = V08 + V09; Out[1] = V12 + V13; Out[2] = 0.461939766255643f * V10 + 0.191341716182545f * V11; Out[3] = V16 - V17; Out[4] = V08 - V09; Out[5] = V16 + V17; Out[6] = 0.191341716182545f * V10 - 0.461939766255643f * V11; Out[7] = V14 + V15; }
修改后的代码只有26次加法及16次乘法,减少了6次乘法。
加速的另外一个部分就是,原先的方法是沿着列方向更新权重和累加值,新的算法更改为行方向更新权重和累加值,这里自然的就变为了缓存友好的方式了。当然其中,会增加一部分内存占用。
原先的处理方式如下:
for (int X = 0; X < Width - 7; X += Step) { for (int Y = 0; Y < Height; Y++) { IM_Convert8ucharTo8float_PureC(Src + Y * Stride + X, DctIn + Y * 8); // 把一整列的字节数据转换为浮点数 } for (int Y = 0; Y < Height; Y++) { IM_DCT1D_8x1_GT_C(DctIn + Y * 8, DctIn + Y * 8); } for (int Y = 0; Y < Height - 7; Y += Step) { IM_DCT2D_8x8_With1DRowDCT_GS_PureC(DctIn + Y * 8, DctOut); // DCT变换 IM_DctThreshold8x8_PureC(DctOut, Threshold); // 阈值处理 IM_IDCT2D_8x8_GS_PureC(DctOut, DctOut); // 在反变换回来 IM_UpdateSum8x8_PureC(Sum + Y * Width + X, DctOut, Width); // 更新权重和阈值 } } IM_SumDivWeight2uchar8x8_PureC(Sum, Dest, Width, Height, Stride, FastMode);
更改后的方案为:
// 先把所有的字节数据转换为浮点数 for (int Y = 0; Y < Height; Y++) { IM_ConvertU8To32F_PureC(Src + Y * Stride, SrcF + Y * Width, Width); } // 因为后面进行了以y为起点,连续8个元素的行方向的DCT变换,所以最后7个点也是有取样的 for (int Y = 0; Y < Height - 7; Y += Step) { float* SumL = Sum + Y * Width; // 8行数据的一维列DCT变换,保存到DctIn中 IM_DCT1D_8xW_C_PureC(SrcF + Y * Width, DctIn, Width); // 把列DCT变换的数据转置下 IM_TransposeF_PureC(DctIn, DctInT, Width, 8); // 进行了以X为起点,X方向连续7个列方向的DCT列变换,所以列方向最后7个元素也能取样到 for (int X = 0; X < Width - 7; X += Step) { // 可以重复利用行方向的转置数据 IM_DCT1D_8x8_C_PureC(DctInT + X * 8, DctOut); // 转换后的数据还要转置 IM_Transpose8x8F_W8_PureC(DctOut, DctOut); // 阈值处理 IM_DctThreshold8x8_PureC(DctOut, Threshold); // 在反变换回来 IM_IDCT2D_8x8_PureC(DctOut, DctOut); // 更新权重和阈值 IM_UpdateSum8x8_PureC(SumL + X, DctOut, Width); } } IM_SumDivWeight2uchar8x8_PureC(Sum, Dest, Width, Height, Stride, FastMode);
具体的细节还需要大家自己慢慢悟。
对于16*16的DCT,本身的计算量就特别夸张,原先论文配套的代码也有提供,但是同样的道理那里的代码存在大量的可节省计算,很多乘法部分可以合并的。优化后的DCT16*16共需要46次乘法72次加法,16*16的去噪程度更强,同样的Sigma参数结果会更加模糊,为了提高16*16的速度,也可以仿照8*8的方式,加大取样间隔,实际测试间隔调整为2个像素,对结果基本没影响,如果把间隔调整为4个像素,在加大的Sigma时,可以较为明显的看到局部的方格,这个应该是不能忍受的, 实际测试如果把间距调整为3个像素,其实结果和原始的还是能承受的,而且加速也很客观。
论文里提到的棋格取样,虽然有一定的理论正确性,但是实际不太可操作,首先是获取满足网格布置的坐标本身就是一个比较慢的过程,第二个即使获取了网格坐标,因为这些坐标分布基本不是按照先X方向增加,再Y方向增加的布局方式布置的,所以为了利用后续的加速技巧,还要先对他们进行排序,这个增加的耗时也是非常客观的,所以我个人觉得那个只具有理论意义。
另外一个就是关于SSE和AVX加速的部分,这里AVX起到的加速作用不是特别明显,核心原因估计还是内存加载和保存占比在整个过程中比较多,而且在计算部分,也曾尝试用FMA相关指令替代mul+add,也不见有明显的收益。 另外,对于算法中经常使用的8*8转置,AVX版本如果学SSE那种直接处理,加速就更有限了。但是AVX里有不同的port,如果充分利用这个则还不错。
多线程:
因为这个DCT算法其实也是领域算法,所以不太好直接使用多线程进行处理,但是还是有办法,对于灰度图像,一种方法是按照高度或者宽度方向分块,但是分块的时候需要注意块和块之间必须有重叠,以保证边缘的不分被充分处理,虽然重叠会增加那么一丢丢的耗时,但是这不算啥,而对于彩色图像,因为要把彩色图分单通道后再调用单通道的处理算法,所以一个自然的想法就是分解后的单通道之间开三个线程并行就可以了。一个简单的代码如下:
int IM_DCT_Denoising_8x8_MultiThread_SSE(unsigned char* Src, unsigned char* Dest, int Width, int Height, int Stride, float Sigma, bool FastMode) { int Channel = Stride / Width; if ((Src == NULL) || (Dest == NULL)) return IM_STATUS_NULLREFRENCE; if ((Width <= 7) || (Height <= 7) || (Sigma <= 0)) return IM_STATUS_INVALIDPARAMETER; if ((Channel != 1) && (Channel != 3)) return IM_STATUS_NOTSUPPORTED; int Status = IM_STATUS_OK; if (Width < 256) { return IM_DCT_Denoising_8x8_SSE(Src, Dest, Width, Height, Stride, Sigma, FastMode); } else { if (Channel == 3) { int StatusA = IM_STATUS_OK, StatusB = IM_STATUS_OK, StatusC = IM_STATUS_OK; unsigned char* Blue = (unsigned char*)malloc(Width * Height * sizeof(unsigned char)); unsigned char* Green = (unsigned char*)malloc(Width * Height * sizeof(unsigned char)); unsigned char* Red = (unsigned char*)malloc(Width * Height * sizeof(unsigned char)); if ((Blue == NULL) || (Green == NULL) || (Red == NULL)) { Status = IM_STATUS_OUTOFMEMORY; goto FreeResource; } IM_SplitRGB(Src, Blue, Green, Red, Width, Height, Stride, 0); #pragma omp parallel sections num_threads(3) { #pragma omp section { StatusA = IM_DCT_Denoising_8x8_SSE(Blue, Blue, Width, Height, Width, Sigma, FastMode); if (StatusA != IM_STATUS_OK) Status = StatusA; } #pragma omp section { StatusB = IM_DCT_Denoising_8x8_SSE(Green, Green, Width, Height, Width, Sigma, FastMode); if (StatusB != IM_STATUS_OK) Status = StatusB; } #pragma omp section { StatusC = IM_DCT_Denoising_8x8_SSE(Red, Red, Width, Height, Width, Sigma, FastMode); if (StatusC != IM_STATUS_OK) Status = StatusC; } } if (Status != IM_STATUS_OK) goto FreeResource; IM_CombineRGB(Blue, Green, Red, Dest, Width, Height, Stride, 0); FreeResource: if (Blue != NULL) free(Blue); if (Green != NULL) free(Green); if (Red != NULL) free(Red); return Status; } else if (Channel == 1) { // 大图分三个线程处理,因为在10年的电脑上,可能很多还是4核,要留一个核给操作系统比较好 int BlockSize = Width / 3; int BlockA_W = BlockSize + 7; // 1/3宽度在加上右侧多7个像素,能完整的计算出左侧BlockSize大小的信息 int BlockB_W = BlockSize + 14; // 1/3宽度在加上左右两侧各7个像素,能完整的计算出中间的BlockSize大小的信息 int BlockC_W = Width - BlockSize - BlockSize + 7; // 1/3宽度在加上左侧多7个像素,能完整的计算出右侧BlockSize大小的信息(注意宽度不一定能整除,所以要用总宽度减去2倍的1/3大小 int StatusA = IM_STATUS_OK, StatusB = IM_STATUS_OK, StatusC = IM_STATUS_OK; unsigned char* BlockA = (unsigned char*)malloc(BlockA_W * Height * sizeof(unsigned char)); unsigned char* BlockB = (unsigned char*)malloc(BlockB_W * Height * sizeof(unsigned char)); unsigned char* BlockC = (unsigned char*)malloc(BlockC_W * Height * sizeof(unsigned char)); if ((BlockA == NULL) || (BlockB == NULL) || (BlockC == NULL)) { Status = IM_STATUS_OUTOFMEMORY; goto FreeMemory; } #pragma omp parallel sections num_threads(3) { #pragma omp section { // 拷贝左侧数据到临时内存 for (int Y = 0; Y < Height; Y++) { memcpy(BlockA + Y * BlockA_W, Src + Y * Stride, BlockA_W * sizeof(unsigned char)); } StatusA = IM_DCT_Denoising_8x8_SSE(BlockA, BlockA, BlockA_W, Height, BlockA_W, Sigma, FastMode); if (StatusA != IM_STATUS_OK) { Status = StatusA; } else { // 把数据复制回去 for (int Y = 0; Y < Height; Y++) { memcpy(Dest + Y * Stride, BlockA + Y * BlockA_W, BlockSize * sizeof(unsigned char)); } } } #pragma omp section { for (int Y = 0; Y < Height; Y++) { memcpy(BlockB + Y * BlockB_W, Src + Y * Stride + BlockSize - 7, BlockB_W * sizeof(unsigned char)); } StatusB = IM_DCT_Denoising_8x8_SSE(BlockB, BlockB, BlockB_W, Height, BlockB_W, Sigma, FastMode); if (StatusB != IM_STATUS_OK) { Status = StatusB; } else { for (int Y = 0; Y < Height; Y++) { memcpy(Dest + Y * Stride + BlockSize, BlockB + Y * BlockB_W + 7, BlockSize * sizeof(unsigned char)); } } } #pragma omp section { for (int Y = 0; Y < Height; Y++) { memcpy(BlockC + Y * BlockC_W, Src + Y * Stride + 2 * BlockSize - 7, BlockC_W * sizeof(unsigned char)); } StatusC = IM_DCT_Denoising_8x8_SSE(BlockC, BlockC, BlockC_W, Height, BlockC_W, Sigma, FastMode); if (StatusC != IM_STATUS_OK) { Status = StatusC; } else { for (int Y = 0; Y < Height; Y++) { memcpy(Dest + Y * Stride + 2 * BlockSize, BlockC + Y * BlockC_W + 7, (Width - 2 * BlockSize) * sizeof(unsigned char)); } } } } FreeMemory: if (BlockA != NULL) free(BlockA); if (BlockB != NULL) free(BlockB); if (BlockC != NULL) free(BlockC); return Status; } } return Status; }
以上代码灰度图也是使用了3个线程,注意在中间块部分呢,两边都要进行适当的扩展,否则会形成一条比较明显的分界线,多线程加速也不是线性,开三个线程也是无法得到3倍加速的,大约为2倍左右的速度提升。
就这么个算法,我把所有的可能旋向都做了实现,轻轻松松就弄了进7000行代码,也是会折腾。
现在年龄大了,感觉有的时候确实是折腾不动了,新的技术在不断发展,而我们依旧趴在老旧的技术上啃食。 不过呢也无所谓,20年前的CS1.6,占地1942,星际争霸现在玩起来还是有那种感觉。
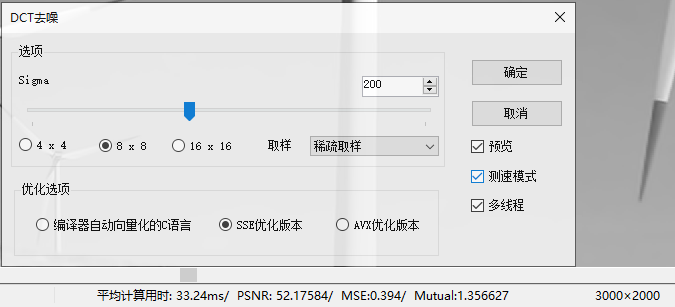
该算法在最新的Demo中已经更新,相关界面如上图所示,下载地址:https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar


 浙公网安备 33010602011771号
浙公网安备 33010602011771号