08-17考试总结

~~长者生日快乐~~

整数数列的解码

请叫我傻逼
看到这张图片就跟气管里塞满灭火器的干粉一样难受
考过的原题，上次怎么错，这次还怎么错
又是用 vis[] 打标记删除……然后就被出题人轻松卡飞
这种删除方法会让你的复杂度变为链长 \(\times\) 链的个数
于是，\(1\) 个特别长的链 \(+\) 很多个特别短的链就能使你的程序当场暴毙
正确的方法是：用链表存，用链表的方式删除
删除的时候要考虑链表优化，别再犯了……

/*************************************************************************
    > File Name: 整数序列的解码.cpp
    > Author: Typedef 
    > Mail: 1815979752@qq.com 
    > Created Time: 2021-08-17 07:59:52
    > blog: https://www.cnblogs.com/Illyasviel
 ************************************************************************/
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+7;
int m,n;
int b[N];
bool h[N];
int nxt[N];
int lst[N]; 
vector<int> v[N];
template<typename T>inline void read(T &n){
    T w=1;n=0;char ch=getchar();
    while(!isdigit(ch)&&ch!=EOF){if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)&&ch!=EOF){n=(n<<3)+(n<<1)+(ch&15);ch=getchar();}
    n*=w;
}
inline void write(int x){
    if (x < 0) x = ~x + 1, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
int main(){
    read(m);
    for(register int i=1;i<=m;i++){
        read(b[i]);
        if(b[i]==-1) ++n;
    }
    if(m==n){
        cout<<n<<endl;
        for(int i=1;i<=n;i++) puts("0");
        return 0;
    }
    for(register int i=1;i<=n;i++){
        nxt[i]=i+1;
        lst[i]=i-1;
    }
    lst[1]=n;
    nxt[n]=1;
    int i=1,j=1;
    for(j=1;j;j=nxt[j]){
        if(i==m+1) break;
        if(b[i]==-1){
            nxt[lst[j]]=nxt[j];
            lst[nxt[j]]=lst[j];
        }
        else v[j].push_back(b[i]);
        i++;
    }
    write(n);
    puts("");
    for(register int i=1;i<=n;i++){
        write(v[i].size());
        cout<<" ";
        for(int j=0;j<v[i].size();j++){
            write(v[i][j]);
            cout<<" ";
        }
        puts("");
    }
    return 0;
}

优秀的子集

我太笨了，考试的时候没有想到正解，写了个暴力还挂了
这题的状态设计很巧妙
首先对坐标离散化，然后按右端点从小到大排序，然后分别处理每个连通的段
f[i][j] 表示处理了前 \(i\) 段线段，覆盖了起始到 \(j\) 的段（由于是实数段，所以表示的区间是 \([st,j)\) 的方案数。
那么如何转移呢？我们分为以下几种情况：
1. 不选择这段线段，什么都没有变化，f[i][j]←+f[i−1][j] 。
2. 选择这段线段，设这条线段为 \([l,r)\) ，分 \(j\) 的值分类讨论。
3. 若 \(j<l\) 则选择后还是只能覆盖起始到 \(j\) 的段，f[i][j]←+f[i−1][j] 。
4. 若 \(l≤j<r\) ，选择后这段状态不存在（因为最后一个位置扩张到了 \(r\) ），f[i][j]←+0。
5. 若 \(j=r\) ，所有 \(l≤k≤r\) 的 \(k\) 都扩张过来到 \(r\) ，所以有 f[i][j]\(←+∑^r_{k=1}\)f[i−1][k]
可以使用滚动数组优化掉第一维
对数组的区间乘、区间求和、单点修改可以用线段树实现

/*************************************************************************
    > File Name: 优秀的子集.cpp
    > Author: Typedef 
    > Mail: 1815979752@qq.com 
    > Created Time: 2021-08-17 11:01:37
    > blog: https://www.cnblogs.com/Illyasviel
 ************************************************************************/                           
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e5+7;
const int mod=98244353;
template<class T>void qread(T &x){
    x=0;bool f=0;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
    if(f) x=-x;
}
int l[N],r[N];
int c[N<<1],mx[N<<1];
vector<int> p[N];
struct Sgt{
    int l,r;
    int sum,mul;
}tr[N<<2];
void build(int p,int l,int r){
    tr[p].mul=1;
    tr[p].l=l,tr[p].r=r;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
    return;
}
void pushup(int p){
    tr[p].sum=(tr[p<<1].sum+tr[p<<1|1].sum)%mod;
    return;
}
void pushdown(int p){
    if(tr[p].mul!=1){
        tr[p<<1].mul=1ll*tr[p<<1].mul*tr[p].mul%mod;
        tr[p<<1].sum=1ll*tr[p<<1].sum*tr[p].mul%mod;
        tr[p<<1|1].mul=1ll*tr[p<<1|1].mul*tr[p].mul%mod;
        tr[p<<1|1].sum=1ll*tr[p<<1|1].sum*tr[p].mul%mod;
        tr[p].mul=1;
    }
    return;
}
void modify1(int p,int k,int d){
    if(tr[p].l==tr[p].r){
        tr[p].sum=(tr[p].sum+d)%mod;
        return;
    }
    pushdown(p);
    int mid=(tr[p].l+tr[p].r)>>1;
    if(k<=mid) modify1(p<<1,k,d);
    else modify1(p<<1|1,k,d);
    pushup(p);
}
void modify2(int p,int l,int r){
    if(l<=tr[p].l&&tr[p].r<=r){
        tr[p].mul=1ll*tr[p].mul*2%mod;
        tr[p].sum=1ll*tr[p].sum*2%mod;
        return;
    }
    pushdown(p);
    int mid=(tr[p].l+tr[p].r)>>1;
    if(l<=mid) modify2(p<<1,l,r);
    if(r>mid) modify2(p<<1|1,l,r);
    pushup(p);
}
int query(int p,int l,int r){
    if(l<=tr[p].l&&r>=tr[p].r) return tr[p].sum;
    pushdown(p);
    int mid=(tr[p].l+tr[p].r)>>1;
    int res=0;
    if(l<=mid) res=(res+query(p<<1,l,r))%mod;
    if(r>mid) res=(res+query(p<<1|1,l,r))%mod;
    return res%mod;
}
int n;
int tot=0;
ll ans=1;
int main(){
    qread(n);
    for(int i=1;i<=n;i++) qread(l[i]),qread(r[i]),c[++tot]=l[i],c[++tot]=r[i];
    sort(c+1,c+tot+1);
    tot=unique(c+1,c+tot+1)-c-1;
    for(int i=1;i<=n;i++){
        l[i]=lower_bound(c+1,c+tot+1,l[i])-c;
        r[i]=lower_bound(c+1,c+tot+1,r[i])-c;
        p[l[i]].push_back(r[i]),mx[l[i]]=max(mx[l[i]],r[i]);
    }
    for(int i=1;i<=tot;i++) mx[i]=max(mx[i],mx[i-1]);
    mx[tot+1]=tot+1;
    build(1,1,tot);
    for(int i=1;i<=tot+1;i++){
        if(mx[i-1]<i) if(i-1) ans=ans*query(1,mx[i-1],mx[i-1])%mod;
        for(auto it:p[i]){
            modify2(1,it,tot);
            int res=it>i?query(1,i,it-1):0;
            modify1(1,it,res+(mx[i-1]<i));
        }
    }
    printf("%lld\n",ans);
    return 0;
}

传统艺能

或许是一个打表找规律题？
没什么好说的，多练才能更快速的发现规律
你会发现答案为：

/*************************************************************************
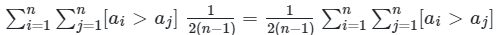
    > File Name: 传统艺能.cpp
    > Author: Typedef 
    > Mail: 1815979752@qq.com 
    > Created Time: 2021-08-17 10:19:45
    > blog: https://www.cnblogs.com/Illyasviel
 ************************************************************************/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+7;
const ll mod=998244353;
ll a[N];
ll n,m;
ll k=0;
ll qpow(ll a,ll b){
    ll res=1;
    while(b){
        if(b&1) res=(res*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return res?res:mod;
}
int main(){
    scanf("%lld",&n);
    m=n>>1ll;
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    sort(a+1,a+n+1);
    a[n+1]=-19260817;
    ll lst=a[1],cnt=1;
    ll inv2=qpow(2,mod-2);
    for(int i=2;i<=n+1;i++){
        if(a[i]==lst) cnt++;
        else{
            if(cnt>1) k=(k+((cnt*(cnt-1)%mod)*inv2)%mod)%mod;
            lst=a[i],cnt=1;
        }
    }
    printf("%lld\n",(((m*inv2)%mod)-k*qpow((4*m-2),mod-2)%mod+mod)%mod);
    return 0;
}

虚灵法师

考场上依然没写出来，甚至没怎么看
这是一道十分有趣的线段树二分题
性质：不管在那个位置降落，最终都要打败所有的怪物，因此只需要考虑用了几次『轮回』
先考虑无修改的情况。设 \(f_x\) 为 \(x\) 降落需要最少几次『轮回』技能。
假设在 \(x\) 位置降落、不使用『轮回』技能能够拓展的极长区间为\([l_x+1,r_x−1]\)，则有\(a_{l_x}>a_x\)，\(a_{r_x}>a_x\)。拓展到这个区间后用一次『轮回』技能。假设\(a_{l_x}<a_{r_x}\)，那么此时法杖的攻击力重置为 \(a_{l_x}\) 。注意到 \(∀j∈[l_x+1,x]\) ， \(a_{l_x}>a_j\) ，所以用好『轮回』技能后能够拓展的极长区间为 \([l_{l_x}+1,r_{l_x}−1]\) ，恰好是 \(l_x\)降落的情况。所以 \(f_x=f_{l_x}+1\) 。
所以算法流程是：先用单调栈求出 \(l_x\) 和 \(r_x\)，求 \(fx\) 时考虑 \(a_{l_x}\) 和 \(a_{r_x}\) 的大小关系从小的一侧转移，如果两者一样大则从两侧转移，可以使用记忆化搜索，最后前缀和存储答案。
考虑带修改的情况，先用无修改的方法算出初始局面的答案。
设 \(A_x\) 表示 \(a_1,a_2,⋯a_x\) 序列的后缀最大值集合， \(B_x\) 表示 \(a_x,a_x+1,⋯,a_n\) 的前缀最大值集合，那么 \(f_x=|A_x⋃B_x|−1\) 。
剩下的：👇
细节不少，码量很大
太**的难写了！！

/*************************************************************************
    > File Name: 虚灵巫师.cpp
    > Author: Typedef 
    > Mail: 1815979752@qq.com 
    > Created Time: 2021-08-17 19:46:47
    > blog: https://www.cnblogs.com/Illyasviel
 ************************************************************************/
//我自己写不出来
//大量参考了Azusa的代码，不过确实是我一个字一个字写的
//属于边写边懂的类型
//目前代码主体是对的，但是还是又错误没调出来
#include<bits/stdc++.h>
#define INF 0x7fffffff
using namespace std;
typedef long long ll;
const int N=2e5+7;
int n,top=0;
int a[N],L[N],R[N];
int stk[N],p[N];
int f[N];
ll s[N];
template<class T>void qread(T &x){
    x=0;bool f=0;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
    if(f) x=-x;
}
bool cmp(int x,int y){
    return a[x]>a[y];
}
struct Sgt1{
    int mx[N<<2];
    void pushup(int p){
        mx[p]=mx[p<<1]+mx[p<<1|1];
        return;
    }
    void build(int p,int l,int r){
        if(l==r){
            mx[p]=a[l];
            return;
        }
        int mid=(l+r)>>1;
        build(p<<1,l,mid),build(p<<1|1,mid+1,r);
        pushup(p);
    }
    //线段树二分
    int get_pre(int p,int l,int r,int pos,int val){
        if(mx[p]<val) return -1;
        if(l==r) return l;
        int mid=(l+r)>>1;
        if(pos<=mid) return get_pre(p<<1,l,mid,pos,val);
        int res=get_pre(p<<1|1,mid+1,r,pos,val);
        if(~res) return res;
        else return get_pre(p<<1,l,mid,pos,val);
    }
    int get_nxt(int p,int l,int r,int pos,int val){
        if(mx[p]<val) return -1;
        if(l==r) return l;
        int mid=(l+r)>>1;
        if(pos>mid) return get_pre(p<<1|1,mid+1,r,pos,val);
        int res=get_nxt(p<<1,l,mid,pos,val);
        if(~res) return res;
        return get_nxt(p<<1|1,mid+1,r,pos,val);
    }
    void modify(int p,int l,int r,int pos,int val){
        if(l==r){
            mx[p]=val;
            return;
        }
        int mid=(l+r)>>1;
        if(pos<=mid) modify(p<<1,l,mid,pos,val);
        else modify(p<<1|1,mid+1,r,pos,val);
        pushup(p);
    }
}tr1;
struct Sgt2{
    ll sum[N<<2],add[N<<2];
    void pushup(int p){
        sum[p]=sum[p<<1]+sum[p<<1|1];
        return;
    }
    void build(int p,int l,int r){
        if(l==r){
            sum[p]=f[l];
            return;
        }
        int mid=(l+r)>>1;
        build(p<<1,l,mid),build(p<<1|1,mid+1,r);
        pushup(p);
    }
    void update(int p,int l,int r,int val){
        sum[p]+=1ll*(r-l+1)*val;
        add[p]+=val;
        return;
    }
    void pushdown(int p,int l,int r){
        if(add[p]){
            int mid=(l+r)>>1;
            update(p<<1,l,mid,add[p]);
            update(p<<1|1,mid+1,r,add[p]);
            add[p]=0;
        }
    }
    void modify(int p,int l,int r,int ql,int qr,int val){
        if(ql<=l&&qr>=r){
            update(p,l,r,val);
            return;
        }
        if(l!=r) pushdown(p,l,r);
        int mid=(l+r)>>1;
        if(ql<=mid) modify(p<<1,l,mid,ql,qr,val);
        if(qr>mid) modify(p<<1|1,mid+1,r,ql,qr,val);
        return;
    }
    ll query(int p,int l,int r,int ql,int qr){
        if(ql<=l&&qr>=r) return sum[p];
        if(l!=r) pushdown(p,l,r);
        ll res=0;
        int mid=(l+r)>>1;
        if(ql<=mid) res+=query(p<<1,l,mid,ql,qr);
        if(qr>mid) res+=query(p<<1|1,mid+1,r,ql,qr);
        return res;
    }
    void solve(int x,int y){
        modify(1,1,n,x,x,-query(1,1,n,x,x)+y);
        return;
    }
}tr2;
int main(){
    int k,op;
    int l,r,x;
    qread(n),qread(k);
    for(int i=1;i<=n;i++) qread(a[i]),p[i]=i;
    stk[++top]=1;
    for(int i=2;i<=n;i++){
        while(top&&a[stk[top]]<=a[i]) top--;
        L[i]=stk[top];
        stk[++top]=i;
    }
    top=0;
    stk[++top]=n;
    for(int i=n-1;i;i--){
        while(top&&a[stk[top]]<=a[i]) top--;
        R[i]=stk[top];
        stk[++top]=i;
    }
    sort(p+1,p+n+1,cmp);
    f[0]=f[n+1]=-1,a[0]=a[n+1]=INF;
    for(int i=1;i<=n;i++) f[p[i]]=f[(a[L[p[i]]]<a[R[p[i]]])?L[p[i]]:R[p[i]]+1];
    tr2.build(1,1,n),tr1.build(1,1,n);
    while(~scanf("%d",&op)){
        if(op&1){
            qread(x);
            if(a[x]==a[x+1]) continue;
            int res=min(a[x],a[x+1]);
            int pre,nxt;
            pre=(x==1)?0:tr1.get_pre(1,1,n,x-1,res);
            nxt=(x+1==n)?n+1:tr1.get_nxt(1,1,n,x+2,res);
            if(!(~pre)) pre=0;
            if(!(~nxt)) nxt=n+1;
            int fl=a[x]<a[x+1]?1:-1;
            if(a[pre]!=res&&pre!=x-1) tr2.modify(1,1,n,pre+1,x-1,-fl);
            if(a[nxt]!=res&&nxt!=x+2) tr2.modify(1,1,n,x+2,nxt-1,fl);
            if(fl>0){
                int idx;
                pre=(x-1)?tr1.get_pre(1,1,n,x-1,a[x+1]+1):0;
                nxt=(x+1==n)?n+1:tr1.get_nxt(1,1,n,x+2,a[x+1]+1);
                if(!(~pre)) pre=0;
                if(!(~nxt)) nxt=n+1;
                if(a[pre]<a[nxt]) idx=pre?tr2.query(1,1,n,pre,pre):-1;
                else idx=(nxt==n+1)?-1:tr2.query(1,1,n,nxt,nxt);
                idx++;
                tr2.solve(x,idx);
                nxt=(x+1==n)?n+1:tr1.get_nxt(1,1,n,x+2,a[x]+1);
                if(!(~nxt)) nxt=n+1;
                if(a[x+1]>a[nxt]) idx=(nxt==n+1)?-1:tr2.query(1,1,n,nxt,nxt);
                tr2.solve(x+1,idx+1);
            }
            else{
                int idx;
                pre=(x-1)?tr1.get_pre(1,1,n,x-1,a[x]+1):0;
                nxt=(x+1==n)?n+1:tr1.get_nxt(1,1,n,x+2,a[x]+1);
                if(!(~pre)) pre=0;
                if(!(~nxt)) nxt=n+1;
                if(a[pre]<a[nxt]) idx=pre?tr2.query(1,1,n,pre,pre):-1;
                else idx=(nxt==n+1)?-1:tr2.query(1,1,n,nxt,nxt);
                idx++;
                tr2.solve(x+1,idx);
                pre=(x==1)?0:tr1.get_pre(1,1,n,x-1,a[x+1]+1);
                if(!(~pre)) pre=0;
                if(a[x]>a[pre]) idx=(!pre)?-1:tr2.query(1,1,n,pre,pre);
                tr2.solve(x,idx+1);
            }
            swap(a[x],a[x+1]);
            tr1.modify(1,1,n,x,a[x]),tr1.modify(1,1,n,x+1,a[x+1]);
        }
        else{
            qread(l),qread(r);
            printf("%lld\n",1ll*tr2.query(1,1,n,l,r)*k+1ll*(r-l+1)*(n-1));
        }
    }
    return 0;
}

posted @ 2021-08-18 08:26 actypedef 阅读(47) 评论(0) 收藏举报

刷新页面返回顶部

actypedef

08-17考试总结

08-17考试总结

整数数列的解码

优秀的子集

传统艺能

虚灵法师

公告