卷积（convolution）与互相关（cross-correlation）比较

卷积和互相关在数学定义上是不一样的；

 

但是，现在大部分的深度学习教程中都把互相关的数学定义，即图像矩阵和卷积核的按位点乘定义为卷积。实际上，这种操作亦应该是互相关（cross-correlation），而卷积需要把卷积核顺时针旋转180度然后再做点乘。

 

数学定义上：

 

 

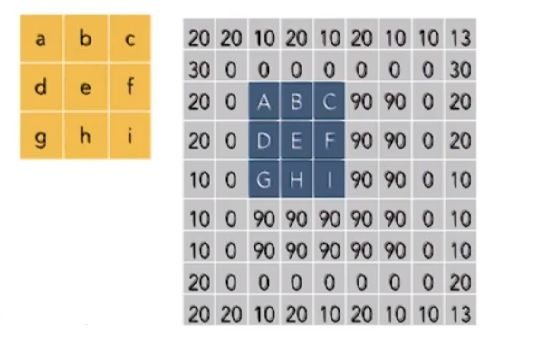
对E点进行互相关操作，结果为：

 

 

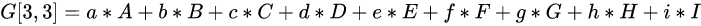
对E点进行卷积操作，结果为：

 

 

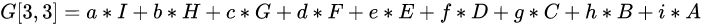
因此，可以理解为卷积是先对卷积核进行了翻转后，再进行对应位置的乘积和求和操作。

这里的翻转是先上下翻转，再左右翻转。

 

特例：当卷积核上下对称，左右对称时，在数学定义上，卷积和互相关结果是一致的。例如:高斯滤波器和均值滤波器。