NOIp2018

　　终于将自己在信息学上的心态调整了过来，来到了第一次NOIp提高 ……

 

停课三个星期　　

　　每天都胡测或者做fjh的神题，成绩波动还在可接受范围内，一点一点地爬上OI这条路，然而每天很茫然，压力还在，负重前行……

 

NOIp Day [-2,-1)

　　参加lgj的模拟，Day1 235，Day2 100。一直都在调整心态，结果对两天的模拟看得太轻，两次模拟赛中都有一个非常显然的错误：思考问题不全面，总会漏掉很多细节，这个错误在NOIp中起码让我少了80分，emm血的教训！

 

NOIp Day -1

　　NOIp前一天的下午，阳光明媚，坐在ll浪，玩手机，死命调整心态。同scx一间房，房号1506，体验还不错，zyc、sc房号1421。

　　出去吃饭，兰州牛肉面，味道平平淡淡，但吃得挺饱^_^

　　晚上回来在1421玩(ﾉ*･ω･)ﾉ到9:00，就回去洗澡睡觉，快睡着的时候lgj来查房！_！，开门第一句lgj问的竟然是睡着了吗！_！，最后大概11点多睡着吧。

 

NOIp Day1

 

早上

　　赖床，6:50的闹钟7:30才出酒店，导致早餐吃的不是很饱，到了广州二中，发现了yhf大佬，%%%%%……

　　

考场

　　Day1的密码：Fei2Xue@Lian$Tian!

　　拿到试题后快速翻了一眼，第一题签到，一看到第二题有点像扩欧就被吓得半死，直接跳过了，第三题马上有了一点点头绪。

 

　　T1

　　题意是，给出一个数列a[1..n]，一种操作：将编号在区间[l..r]的数同时减去x，询问操作完数列中所有数为0的∑x的最小值。

　　样例解释给得太良心了，马上yy出做法，20分钟就做完第一题，9:00都没到。

　　做法：显然对于一个值a，要将它变为0，我们可以考虑不断扩张对它操作的区间，边界就是两个比a小的数，那么我们只要每次找出当前区间的最小值，将该区间减去该最小值，然后这个最小值，将区间割开，然后我们在分别进入分割开的区间，同理统计答案。

 

　　T2

　　题意是，询问集合中有多少个数，任意其它元素的倍数的和都与之不等。

　　刚看到题目还以为是扩欧，然后发现考场很多人都在写T2，感到疑惑，就手推了一下假的大样例，发现好像可以总结成上述要求，然后看了一下时间复杂度，发现80分数据有点太水了，怀着疑惑的心态写了一个不优美的完全背包，结果复杂度被我莫名其妙多写了一个n，然后算了一下时间复杂度，发现后20分我的理论复杂度卡不过，然后想怎么优化，结果并没有发现自己每次把数组清空的愚蠢，然后只能在心中默默祈祷数据水……

　　做法：显然可以想到大的只能由小的组成，那么就可以先将原数列排序，然后从小到大依次加进一个大小为25000的完全背包中，每次判断当前数是否合法即可。

 

　　T3

　　题意是，询问将原树分成m条链，最短链的最大值。

　　最小的最大，套路二分答案，然后考虑怎么合并，然后竟然yy出了贪心合并的方法，然后没过大样例，然后在yy了一下程序的正确性，发现没有保证在最多匹配的情况下贡献一个最大的向上连的值，改了一下贪法过来大样例，认真想了一下发现好像会T，然后就把直径分出来写（35分，这可能是我这道题的最终得分了#_#），我过了大样例所以我丝毫不慌，然后就去认真做T2了。出考场还以为T3 80分稳了，结果我把一条边割成两半了（这竟然能过大样例简直天理难容）！！！！！！！

　　做法：先二分答案，我们对于每一个节点，维护两个值：1、能向上贡献的长度L，2、以该节点为根的子树中能匹配多少条链M。考虑合并，我们要在满足匹配最多条边的情况下，得到最大的L，认真想一下可能可以看出这是一个具有单调性的问题，再次二分贡献哪条边，判断是否能达到最大的匹配数就可以了。

 

下午&晚上

　　半个下午都在zyc和sc房1421玩耍，半个下午会1506看了两部电影，然后就出去吃黄焖鸡，感觉还算可以吧……

　　回来看完了没看完的电影，然后洗澡，结果！_！，停电了，没错，就是在洗澡的时候！_！，绝望，只好快快敷衍完睡觉，快要睡着的时候！_！，电来了！_！，绝望，光明大道，砥砺前行！再次11点多睡着。

 

NOIp Day 2

 

早上

　　没有赖床，早早地去吃早餐，吸取Day1的经验，结果吃得太饱了……

 

考场

　　Day2的密码：%xiao#SHU!shen9XIA

　　快速地过了一遍题目，第一题环套树，第三题又是一棵树，心想好多的树，第二题看起来有点猥琐，就现跳过了。

 

　　T1

　　题意是，对于一个环套树，经过n-1条边，每条边只经过一次，依次遍历整棵树，使得遍历序的字典序最小。

　　因为是一个环套树，所以我们只要找到环考虑割哪条边就行了，结果考场上过于自信以至于没有想到枚举的方法，结果用了一中不全面的贪心来寻找最优的割边方案，虽然过了大样例，但可能会WA掉几个点。

　　做法：对于环套树，我们先将环上的边找出来，因为遍历方案只经过了n-1条边且每条边只经过一次，所以我们枚举环上的边，强制使得该边不能被经过，然后按照一棵树的方法来做，看哪个方案最优就可以了。

　　

　　T2

　　题意有点难以描述，对于一个n*m的格子矩阵，每个格子可以填0/1，只能从当前点往下或往右走，有很多从（1,1）到（n，m）的行走方案，定义行走方案A比行走方案B要大，那么存在一个时刻x，在该时刻时，行走方案A向下走，行走方案B向右走，在该时刻前所有的行走方向都相同。询问有多少不同的填数方案，满足任意两个不同的行走方案，大的行走方案走过的01串的大于或等于小的行走方案走过的01串。

　　考场上对这题毫无头绪，认真地打了前20分的表，然后用状压写了另30分，并没有想到要找规律。

　　做法：打表找规律，然后可以发现，只要把m = n+1的暴力算出来，然后乘3快速幂就可以了。矩阵乘法快速幂的方法还不是很懂……

 

　　T3

　　题意是，对于一棵带权树，每条边两端至少有一个点被标记，有m个询问，每次强制两个点标记或不标记，询问被标记的点的点权和的最小值。

　　考场上想到了先正着dp一遍，然后再反着dp一遍，求两点的lca然后倍增转移，但是考场上认真思考了一下，发现现在我的编程能力想写出来有一点悬，然后就只打了n*m的暴力，emm，编程能力还有待提高。

　　做法：我们可以发现，对于一个询问，我们可以把它分成五个部分：

　　

 

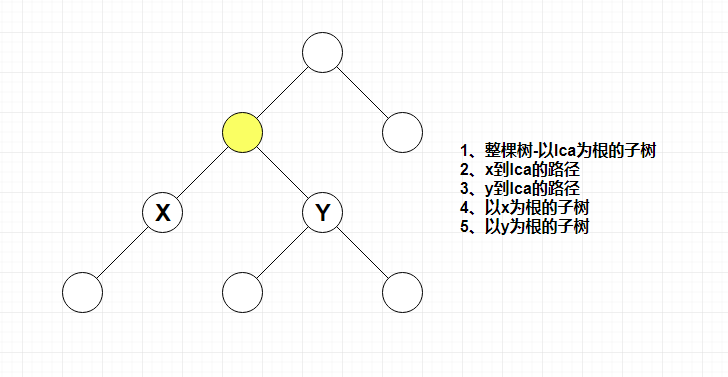
　　显然1、4、5都是可以预处理的，那么我们现在就要来处理2和3。

　　我们需要先预处理出一个数组t[u][v][0/1][0/1]，表示u向上跳1<<v步，u的状态为0/1，v的状态为0/1的花费最小值。

　　预处理完后，就可以在倍增lca的时候直接算出2和3两部分了。

　　贴上3个小时写完的Code：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <cmath>
#include <queue>
#include <set>
#include <map>

using namespace std;

const int N = 200010;
const int M = 25;
const long long oo = 2100000000000LL;

struct ed { int nx, v; } e[(N<<1)];

int tot = 0, he[N];
void add(int u, int v) {
    e[++tot].nx = he[u], e[tot].v = v, he[u] = tot;
}

char tmp[3];

long long t[N][M][2][2];
long long f[N][2], g[N][2];

int val[N], fat[N][M], dep[N], c;

void dfs1(int u, int fa) {
    f[u][0] = 0, f[u][1] = val[u];
    for (int h=he[u]; h!=-1; h=e[h].nx) {
        int to = e[h].v;
        if(to == fa) continue;
        fat[to][0] = u, dep[to] = dep[u] + 1;
        for (int i=1; i<=c; i++)
            if(fat[to][i-1]) fat[to][i] = fat[fat[to][i-1]][i-1];
        dfs1(to, u);
        f[u][0] += f[to][1];
        f[u][1] += min(f[to][0], f[to][1]);
    }
}

void dfs2(int u, int fa) {
    for (int h=he[u]; h!=-1; h=e[h].nx) {
        int to = e[h].v;
        if(to == fa) continue;
        g[to][0] = g[u][1] + f[u][1] - min(f[to][0], f[to][1]);
        g[to][1] = min(g[u][0] + f[u][0] - f[to][1], g[to][0]);
        dfs2(to, u);
    }
}

int n, m;
void solve(int u, int fa) {
    for (int h=he[u]; h!=-1; h=e[h].nx) {
        int to = e[h].v;
        if(to == fa) continue;
        t[to][0][0][1] = f[u][1] - min(f[to][0], f[to][1]);
        t[to][0][1][0] = f[u][0] - f[to][1];
        t[to][0][1][1] = f[u][1] - min(f[to][0], f[to][1]);
        t[to][0][0][0] = oo;
        for (int i=1; i<=c; i++) {
            for (int u=0; u<2; u++)
            for (int v=0; v<2; v++) {
                t[to][i][u][v] = oo;
                for (int w=0; w<2; w++) 
                    t[to][i][u][v] = min(t[to][i][u][v], t[to][i-1][u][w] + t[fat[to][i-1]][i-1][w][v]);
            }
        }
        solve(to, u);
    }
}

long long work(int x, int x1, int y, int y1) {
    
    long long now_x[2] = {oo, oo}, next_x[2] = {oo, oo};
    long long now_y[2] = {oo, oo}, next_y[2] = {oo, oo};
    
    if(dep[x] > dep[y]) swap(x, y), swap(x1, y1);
    now_x[x1] = f[x][x1], now_y[y1] = f[y][y1];
    
    for (int i=c; i>=0; i--) {
        if(dep[fat[y][i]] >= dep[x]) {
            next_y[0] = next_y[1] = oo;
            for (int u=0; u<2; u++)
            for (int v=0; v<2; v++) {
                next_y[v] = min(next_y[v], now_y[u]+t[y][i][u][v]);
            }
            now_y[0] = next_y[0], now_y[1] = next_y[1], y = fat[y][i];    
        }
    }
    
    if(x == y) return g[x][x1] + now_y[x1];
    
    for (int i=c; i>=0; i--) {
        if(fat[x][i] != fat[y][i]) {
            next_x[0] = next_x[1] = oo;
            for (int u=0; u<2; u++)
            for (int v=0; v<2; v++) {
                next_x[v] = min(next_x[v], now_x[u]+t[x][i][u][v]);
            }
            now_x[0] = next_x[0], now_x[1] = next_x[1];
            next_y[0] = next_y[1] = oo;
            for (int u=0; u<2; u++)
            for (int v=0; v<2; v++) {
                next_y[v] = min(next_y[v], now_y[u]+t[y][i][u][v]);
            }
            now_y[0] = next_y[0], now_y[1] = next_y[1];    
            x = fat[x][i], y = fat[y][i];    
        }    
    }
    
    int lca = fat[x][0];
    long long ans1 = g[lca][0] + f[lca][0] - f[x][1] - f[y][1] + now_x[1] + now_y[1];
    long long ans2 = g[lca][1] + f[lca][1] - min(f[x][1], f[x][0]) - min(f[y][1], f[y][0]) + min(now_x[1], now_x[0]) + min(now_y[0], now_y[1]);
    
    return min(ans1, ans2);
}

set <int> s[N];

int main() {
    
    memset(he, -1, sizeof(he));
    
    scanf("%d%d", &n, &m), c = log(n) / log(2);
    scanf("%s", tmp+1);
    for (int i=1; i<=n; i++) scanf("%d", &val[i]);
    for (int i=1; i<n; i++) {
        int u, v; scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
        s[u].insert(v), s[v].insert(u);
    }
    
    dep[1] = 1, dfs1(1, 0), dfs2(1, 0), solve(1, 0);
    
    for (int i=1; i<=m; i++) {
        int x, x1, y, y1;
        scanf("%d%d%d%d", &x, &x1, &y, &y1);
        if(s[x].find(y)!=s[x].end() && !x1 && !y1) { printf("-1\n"); continue; }
        printf("%lld\n", work(x, x1, y, y1));
    }
    
    return 0;
}

 

总结

　　这次比赛总体来讲也在可接受范围内，但有两个非常显然的错误：1、思考问题不够全面  2、编程能力较弱

　　这两个问题，慢慢地练，总能练上去的，^_^

 

　　在OI这条路上连滚带爬走了3年，从NOIp普及走到了提高，从石实走到了石中，纵然有血有泪，离终点仅剩1年，也要不悔地走下去……