CDQ分治
TAP:整体二分查答案,CDQ分治计贡献
引入
对于离线的带有修改与询问的问题背景,若修改很难处理,且修改对询问的贡献能计算并合并,可以考虑使用CDQ分治。
例题:给出一个数字矩阵,每次有两种操作:1、在(x,y)处添加A,查询一个右上角为(x1,y1),左下角为(x2,y2)的矩形中数的和。(题目戳这里)
先贴上CODE:
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; const int N = 5000010; struct ask { int x, y, val, id, ID; }q[N], tmp[N]; int bit[N], ans[N]; void add(int x, int p) { for (;x < N; x += x & -x) bit[x] += p; } int que(int x) { int ans = 0; for (;x; x -= x & -x) ans += bit[x]; return ans; } bool _sort(ask xx, ask yy) { return (xx.x != yy.x) ? (xx.x < yy.x) : (xx.id < yy.id); } void CDQ(int l, int r) { if(l == r) return ; int mid = (l+r)>>1; for (int i=l; i<=r; i++) { if(q[i].id<=mid && !q[i].ID) add(q[i].y, q[i].val); if(q[i].id> mid && q[i].ID) ans[q[i].ID] += que(q[i].y)*q[i].val; } for (int i=l; i<=r; i++) if(q[i].id<=mid && !q[i].ID) add(q[i].y, -q[i].val); int w1 = l, w2 = mid+1; for (int i=l; i<=r; i++) { if(q[i].id<=mid) tmp[w1++] = q[i]; else tmp[w2++] = q[i]; } for (int i=l; i<=r; i++) q[i] = tmp[i]; CDQ(l, mid), CDQ(mid+1, r); } int main() { int tmp1, tmp2; scanf("%d%d", &tmp1, &tmp2); int ki, tot = 0, cnt = 0; while(23) { scanf("%d", &ki); if(ki == 3) break; if(ki == 1) { int xx, yy, vv; scanf("%d%d%d", &xx, &yy, &vv); cnt++, q[cnt].x = xx, q[cnt].y = yy, q[cnt].val = vv, q[cnt].id = cnt, q[cnt].ID = 0; } if(ki == 2) { tot ++; int x1, y1, x2, y2; scanf("%d%d%d%d", &x1, &y1, &x2, &y2); cnt++, q[cnt].x = x1-1, q[cnt].y = y1-1, q[cnt].val = 1, q[cnt].id = cnt, q[cnt].ID = tot; cnt++, q[cnt].x = x1-1, q[cnt].y = y2 , q[cnt].val = -1, q[cnt].id = cnt, q[cnt].ID = tot; cnt++, q[cnt].x = x2 , q[cnt].y = y1-1, q[cnt].val = -1, q[cnt].id = cnt, q[cnt].ID = tot; cnt++, q[cnt].x = x2 , q[cnt].y = y2 , q[cnt].val = 1, q[cnt].id = cnt, q[cnt].ID = tot; } } sort(q+1, q+cnt+1, _sort); CDQ(1, cnt); for (int i=1; i<=tot; i++) printf("%d\n", ans[i]); return 0; }
先大体地讲一下步骤,对于这道题目,我们很容易就发现某些修改会影响到某些询问,那么我们怎样统计出这些贡献呢?
首先用一个容斥原理的小技巧将一个询问分成4块,具体怎么分就直接看程序吧,这需要统计每一块的前缀和,所以只有满足操作的x<=询问的x时,才有可能产生贡献……同整体二分一样,将询问和操作混在一起按照x来排一个序,然后按照id分成两半
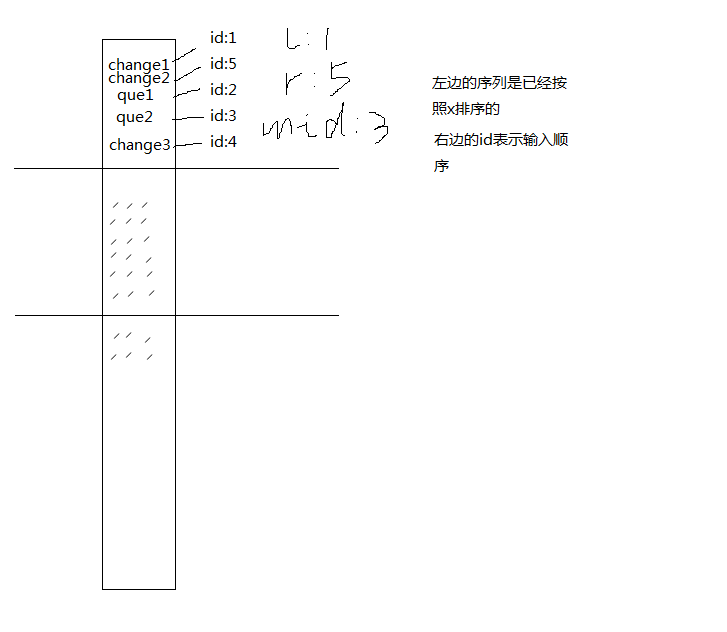
只有id<=mid的操作才会对id>mid的询问产生影响,这是基于按x的排序上,然后再用mid将操作、询问分成两块处理,算贡献的时候,按y来当下标实行增加操作,统计贡献的时候只要用一个树状数组维护前缀和就可以了。
最后整理一下思路:
满足以下条件:
1、操作的x<=询问的x
2、操作的id<=询问的id
3、操作的y<=询问的y
操作对询问才有贡献
我们通过排序处理x这一维,然后用CDQ分治处理了id这一维,最后用下标为y的树状数组维护前缀和处理了y这一维,从而统计处理每一个询问的结果^_^
再放一道例题&_&
对于一个元素,有三个信息:a,b,c,f(j)表示有多少个i满足ai<=aj&&bi<=bj&&ci<=cj。(题目戳这里)
再次贴上CODE
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; const int N = 1000010; struct ask { int x, y, z, id; }q[N], tmp[N]; int bit[N], ans[N]; void add(int x, int p) { for (;x < N; x += x & -x) bit[x] += p; } int que(int x) { int an = 0; for (;x; x -= x & -x) an += bit[x]; return an; } bool _sort1(ask xx, ask yy) { return (xx.x != yy.x) ? (xx.x < yy.x) : ((xx.y != yy.y) ? (xx.y < yy.y) : (xx.z < yy.z)); } bool _sort2(ask xx, ask yy) { return (xx.y != yy.y) ? (xx.y < yy.y) : ((xx.z != yy.z) ? (xx.z < yy.z) : (xx.x < yy.x)); } void CDQ(int l, int r) { if(l == r) return ; int mid = (l+r)>>1; CDQ(l, mid), CDQ(mid+1, r); sort(q+l, q+r+1, _sort2); for (int i=l; i<=r; i++) { if(q[i].x<=mid) add(q[i].z, 1); if(q[i].x> mid) ans[q[i].id] += que(q[i].z); } for (int i=l; i<=r; i++) if(q[i].x<=mid) add(q[i].z, -1); } int same[N], d[N]; int main() { int n, tmp1; scanf("%d%d", &n, &tmp1); for (int i=1; i<=n; i++) { scanf("%d%d%d", &q[i].x, &q[i].y, &q[i].z), q[i].id = i; } sort(q+1, q+n+1, _sort1); for (int i=1; i<=n;) { int j = i+1; while(j <= n && q[i].x == q[j].x && q[i].y == q[j].y && q[i].z == q[j].z) j++; while(i<j) same[q[i++].id] = q[j-1].id; } for (int i=1; i<=n; i++) q[i].x = i; CDQ(1, n); for (int i=1; i<=n; i++) d[ans[same[q[i].id]]] ++; for (int i=0; i<n; i++) printf("%d\n", d[i]); return 0; }
套算法的模板题QAQ。
将这一题的思路整理一下:先按x排序,将x改为1~N的编号,因为相等也是满足关系的,所以我们把一样的记到编号最大的那里(稍微理解一下就行了),具体的做法其实同上一题一样,排序处理掉一维,CDQ分治处理掉一维,最后后缀数组处理掉一维,详见程序^_^。
总结一下CDQ分治,一个操作要在多维有序的情况下才能影响到一个询问时,就可以通过CDQ分治离线降维。
注意!
先放一道题:一个序列,每次删除一个数,求每次删除之前的逆序对个数。(题目戳这里)
这道题的神奇之处在于它有两种贡献的可能(即有两种有序的情况可以影响到询问,这样的话要在分治中分开处理)
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <cmath> using namespace std; const int N = 800010; #define int long long struct Q { int x, y, id; }q[N], tmp1[N], tmp2[N]; int t[N]; void add(int x, int p) { for (;x < N; x += x & -x) t[x] += p; } int que(int x) { int sum = 0; for (;x; x -= x & -x) sum += t[x]; return sum; } int ans[N], n, m; void CDQ(int l, int r) { if(l == r) return ; int w1 = 0, w2 = 0, mid = (l + r) >> 1; for (int i=l; i<=r; i++) { if(q[i].id <= mid) add(q[i].y, 1), tmp1[++w1] = q[i]; else ans[q[i].id] += que(n) - que(q[i].y), tmp2[++w2] = q[i]; } for (int i=l; i<=r; i++) { if(q[i].id <= mid) add(q[i].y, -1); } for (int i=r; i>=l; i--) { if(q[i].id <= mid) add(q[i].y, 1); else ans[q[i].id] += que(q[i].y); } for (int i=l; i<=r; i++) { if(q[i].id <= mid) add(q[i].y, -1); } for (int i=l; i<=l+w1-1; i++) q[i] = tmp1[i-l+1]; for (int i=l+w1; i<=r; i++) q[i] = tmp2[i-l-w1+1]; CDQ(l, l+w1-1), CDQ(l+w1, r); } int ys[N]; signed main() { scanf("%lld%lld", &n, &m); for (int i=1, tmp; i<=n; i++) { scanf("%lld", &tmp); q[i].x = i, q[i].y = tmp, ys[tmp] = i; } int tim = n; for (int i=1, tmp; i<=m; i++) { scanf("%lld", &tmp); q[ys[tmp]].id = tim--; } for (int i=1; i<=n; i++) if(!q[i].id) q[i].id = tim--; CDQ(1, n); for (int i=1; i<=n; i++) ans[i] += ans[i-1]; for (int i=n; i>=n-m+1; i--) printf("%lld\n", ans[i]); return 0; }
练习
洛谷luogu.org 4390
https://www.luogu.org/problemnew/show/P4390
备注:例题
洛谷3810
https://www.luogu.org/problemnew/show/P3810
备注:模板题
洛谷 4169
https://www.luogu.org/problemnew/show/P4169
备注:模板题
Cdq分治+dp
Bzoj4700
https://www.lydsy.com/JudgeOnline/problem.php?id=4700
bzoj1492
https://www.lydsy.com/JudgeOnline/problem.php?id=1492
备注:NOI2007 D1T2
Bzoj3672
https://www.lydsy.com/JudgeOnline/problem.php?id=3672
备注:NOI2014 D2T3




 浙公网安备 33010602011771号
浙公网安备 33010602011771号