莫比乌斯反演

引入 

　　求：

　　

　　为了方便理解接下来要讲的，把上课时做的笔记拍了下来：（Square-Free数就是【不是任何完全平方数（1除外）的倍数的数】（Square-Free数-维基百科）

　　

　　可以用找规律来解决上面的问题，笔记左上角和右上角就是两个特殊的例子，这两个例子的分析如下：

 　　

　　

 

　　根据这两个例子我们可以发现，这很符合容斥的性质，那么我们就可以得到一个容斥原理的式子：

　　

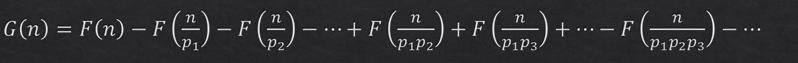
　　那么对这个容斥的式子进行变形，就可以变成以下形式：

　　

 

性质

　　莫比乌斯函数有两个比较重要的性质：

1、积性

　　同样的莫比乌斯函数具有与欧拉函数类似的积性，这个在之前讲欧拉函数的时候有提到（之前的博客），这里就不再提了。根据它的积性性0质，我们可以很轻松地推出如何用线性筛来求欧拉函数，CODE如下：

 

void fanyan() {
    
    miu[1] = 1;
    
    for (int i=2; i<=ma; i++) {
        if(!vis[i]) {
            prime[++tot] = i, miu[i] = -1;
        }
        for (int j=1; j<=tot; j++) {
            
            long long te = i*prime[j];
            
            if(te>ma) break;
            
            vis[te] = 1;
            if(i%prime[j]==0) miu[te] = 0;
            else               miu[te] = miu[i] * (-1);
        }
    }
    
    return ;
}

2、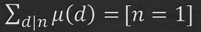

　　这是莫比乌斯函数一个很强大的性质，一般都与约数等等表述几个数之间关系时会用到，这里讲两个栗子方便理解：

栗1：

　　求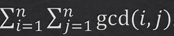，做法如下：

　　

　　

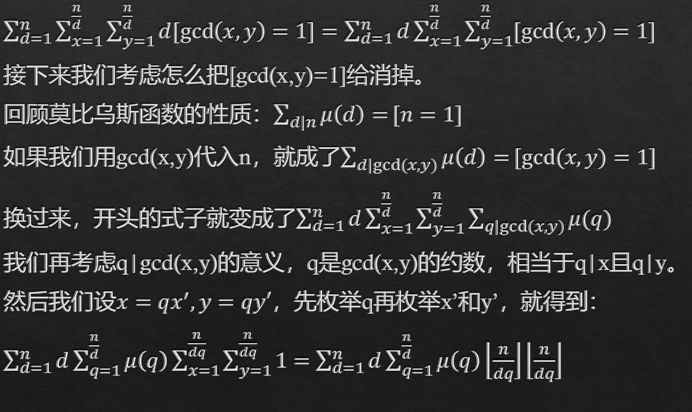
栗2

　　求对于每一对i(1<=i<=N),j(1<=j<=M)的lcm(i, j)的和：

　　　　

 

实现：（主要用到的是分块）

 

　　

　　　　  

CODE：

//BZOJ 3529
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>
#include <vector>
#include <cmath>
#include <queue>

#define sc1(p1) scanf("%d", &p1)
#define sc2(p1, p2) scanf("%d %d", &p1, &p2)
#define sc3(p1, p2, p3) scanf("%d %d %d", &p1, &p2, &p3)

#define pr(p1) printf("%d\n", p1)

using namespace std;

const int maxn = 100010;
const int oo = 2100000000;
const int mod = 1<<30;

int miu[maxn], prime[maxn], tot;
bool vis[maxn];
int ma, bit[maxn];

int query(int x) { int ans=0; for(; x; x-=x&-x) ans+=bit[x]; return ans; }
void add(int x, int y){ for(; x<=ma; x+=x&-x) bit[x]+=y; }

void fanyan() {
    
    miu[1] = 1;
    
    for (int i=2; i<=ma; i++) {
        if(!vis[i]) {
            prime[++tot] = i, miu[i] = -1;
        }
        for (int j=1; j<=tot; j++) {
            
            long long te = i*prime[j];
            
            if(te>ma) break;
            
            vis[te] = 1;
            if(i%prime[j]==0) miu[te] = 0;
            else               miu[te] = miu[i] * (-1);
        }
    }
    
    return ;
}

struct po { int id, nu; } g[maxn];
struct ne { int n, m, a, id; } s[maxn];

bool _sort1(po xx, po yy) { return xx.nu < yy.nu; }
bool _sort2(ne xx, ne yy) { return xx.a < yy.a; }

void Get_F() {
    for (int i=1; i<=ma; i++) g[i].nu = 1, g[i].id=i;
    
     for (int i=2; i<=ma; i++) {
        for (int j=1; j<=ma/i; j++) {
            g[i*j].nu += i;
        }
    }
    
    sort(g+1, g+ma+1, _sort1);
    
    return ;
}

int Get_Num(int x, int y) {
    
    int xx = x*(x+1)/2, yy = y*(y+1)/2;
    return xx * yy;
}

int n, m, a;

int fenkuai1(int nn, int mm) {
    
    int shi = min(nn, mm), ans = 0;
    
    for (int i=1; i<=min(nn, mm);) {
        
        int wh = min(nn/(nn/i), mm/(mm/i));
        int d = query(wh) - query(i-1);
        int tt = (int)(nn/i) * (int)(mm/i);
        ans += d*tt, i = wh+1;
    }
    return ans;
}
int ans[maxn];
int main() {
    
    int T; sc1(T);
    
    ma = 100000;
    
    fanyan();
    Get_F();
    
    for (int i=1; i<=T; i++) {
        sc3(s[i].n, s[i].m, s[i].a);
        s[i].id = i;
    }
    
    sort(s+1, s+T+1, _sort2);
    int tep = 0;
    for (int i=1; i<=T; i++) {
        while(tep < ma && g[tep+1].nu <= s[i].a) {
            tep++;
            for (int j=1; j*g[tep].id<=ma; j++) {
                add(j*g[tep].id, g[tep].nu*miu[j]);
                
            
            }
            
        }
        ans[s[i].id] = fenkuai1(s[i].n, s[i].m);
    }
    
    for (int i=1; i<=T; i++) pr(ans[i]&0x7fffffff);
    
    return 0;
}

 

这里有一道很玄学的题

　　LUOGU3327

 

　　这道题的重点就是下面这一条公式（d[i]表示i的约数个数）:

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

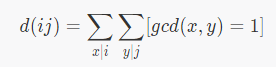
　　这个公式的证明想了好久，才想出一个合理的证明方法：

 

　　首先，我们用质因数相乘的形式来表示i、j（下面的k各不相同）：

 

　　

 

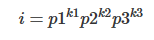
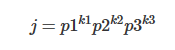
　　一对x，y互质，我们可以认为是为i*j贡献一个这样的约数：

 

　　设t = i中有的所有y中也含有的质因数相乘的积；举个栗子：y = p2的k2次方，那么t = i中的p2的k2次方，

 

　　贡献的约数就是t*y*x。

 

 

 

　　上面的理解了的话，我们就可以套mobius反演了。 

 

 

练习：

BZOJ 2154
BZOJ 3529
BZOJ 2440
BZOJ 2301