非线性方程组解法(一)Newton's method

• 非线性方程组解法(一)Newton's method

format long;

x0=[1,1]';

X=x0;

d=1;

num=0;

F=[1,1]';

while d > 10^(-6)

DF=[2*x0(1)-1,2*x0(2);2*x0(1),-2*x0(2)-1];

F=-[x0(1)^2+x0(2)^2-x0(1);x0(1)^2-x0(2)^2-x0(2)];

s=DF\F;

x1=x0+s;

X=[X,x1];

d=max(abs(x1-x0));

num=num+1;

x0=x1;

end

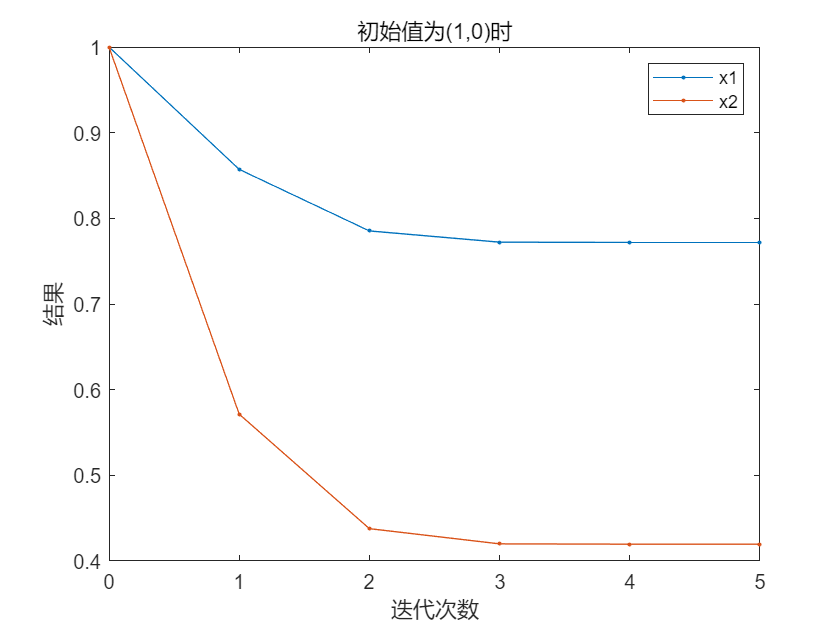
figure

plot(0:num,X,'.-')

xlabel('迭代次数'),ylabel('结果');

legend('x1','x2')

title('初始值为(1,0)时')

syms x1 x2 x3

a=[x1 x2 x3];

F=[-1/81*cos(x1)+1/9*x2^2+1/3*sin(x3)-x1

1/3*sin(x1)+1/3*cos(x3)-x2

-1/9*cos(x1)+1/3*x2+1/6*sin(x3)-x3];

x0=[1,1,1];

[X,num,x0,ERR] = newton(F,a,x0);

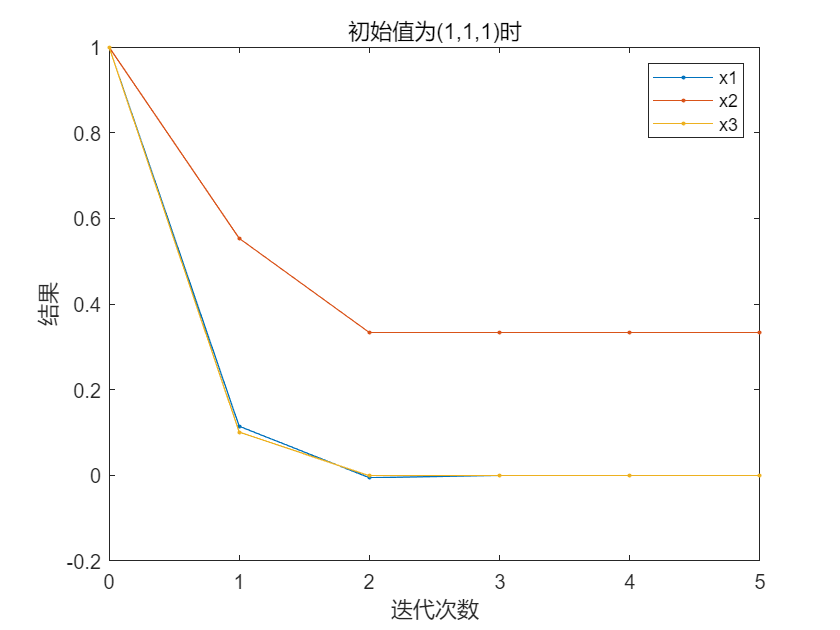
figure(1)

plot(0:num,X','.-');

xlabel('迭代次数'),ylabel('结果');

legend('x1','x2','x3')

title('初始值为(1,1,1)时')

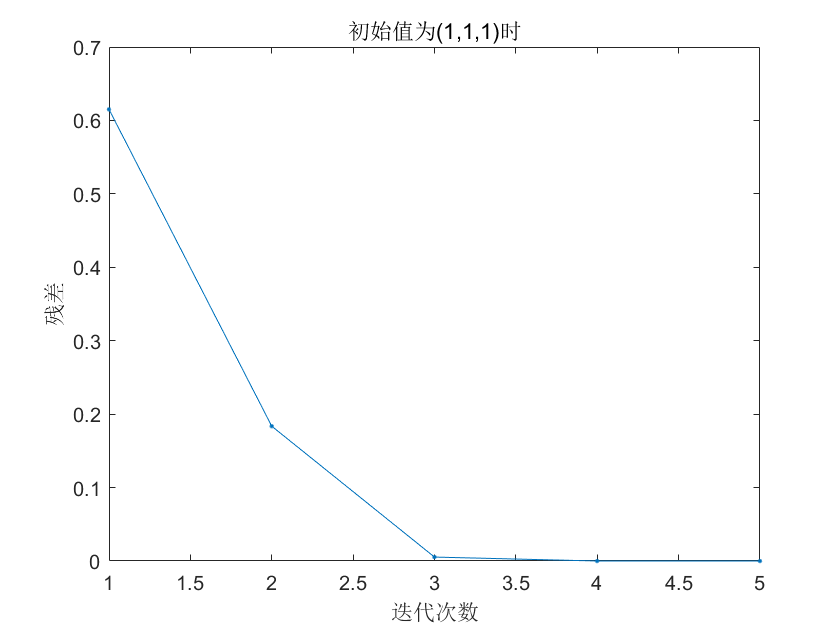
figure(2)

plot(1:num,ERR','.-');

xlabel('迭代次数'),ylabel('残差');

title('初始值为(1,1,1)时')

function [X,num,x0,ERR] = newton(fun,v,x0)

%NEWTON 法求解非线性方程组

DF=jacobian(fun,v);%求雅可比矩阵

X=x0;

num=0;

err=1000;

ERR=[];

while err > 10^(-6)

df=double(subs(DF,v,x0));

f=-double(subs(fun,v,x0));

s=df\f;

x1=x0+s';

X=[X;x1];

Tf=double(subs(fun,v,x0));

err=max(abs(Tf-0));

num=num+1;

x0=x1;

ERR=[ERR,err];

end

end