两点边值问题

微分方程数值解--差分法

problem 1:

考虑如下两点边值问题

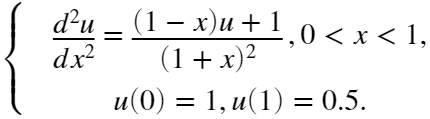
其精确解为：

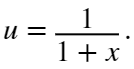
clc

clear all

format long

u=f_1(64);%数值解

x=linspace(0,1,65);

U=1./(1+x);%精确解

figure(1)

plot(x,U,'b-');hold on

plot(x,u,'r.-');

xlabel('x'),ylabel('u');

legend('精确解','数值解')

title('精确解曲线和步长h=1/64时的数值解曲线')

err1=abs(u'-U);

hold off

u2=f_1(128);%数值解

x2=linspace(0,1,129);

U2=1./(1+x2);%精确解

figure(2)

plot(x2,U2,'b-');hold on

plot(x2,u2,'r.-');

xlabel('x'),ylabel('u');

legend('精确解','数值解')

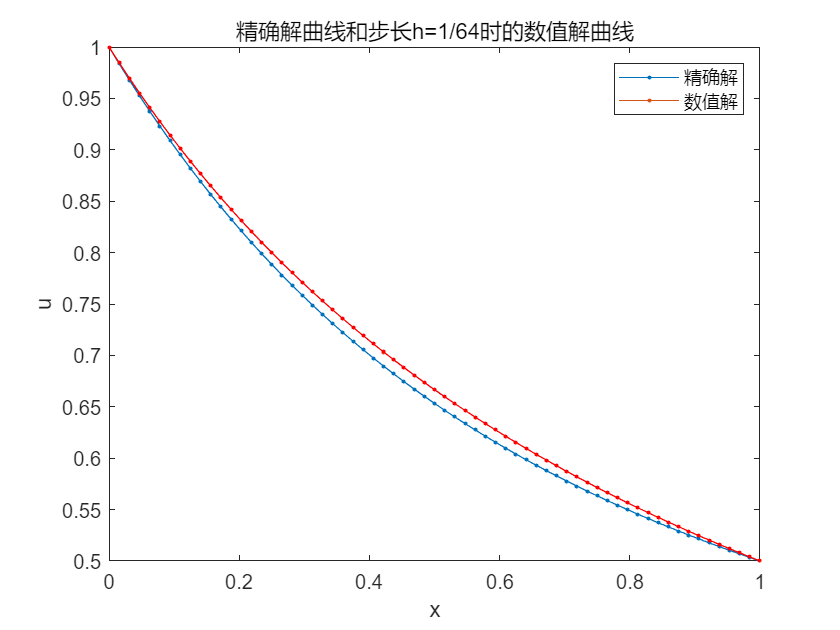
title('精确解曲线和步长h=1/128时的数值解曲线')

err2=abs(u2'-U2);

hold off

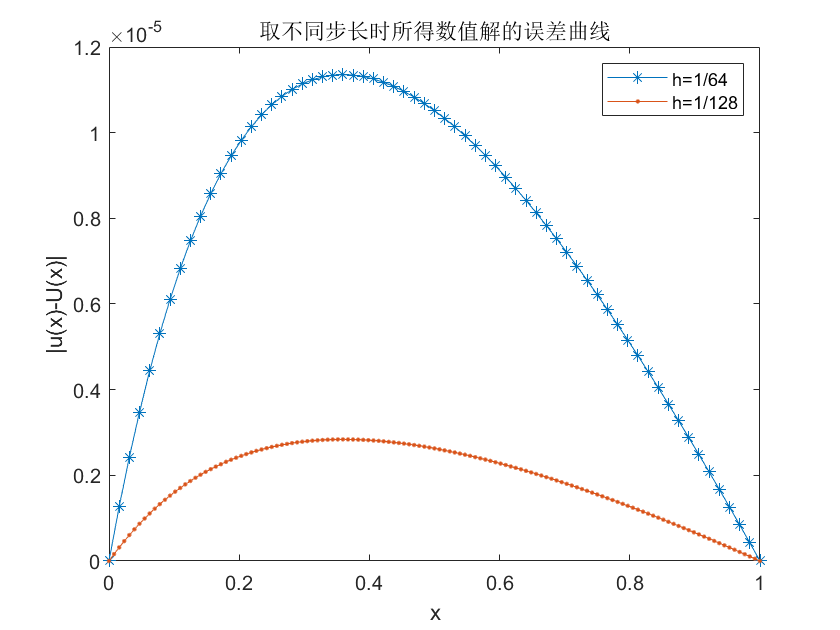
figure(3)

plot(x,err1,'*-');hold on

plot(x2,err2,'.-');

legend('h=1/64','h=1/128')

xlabel('x'),ylabel('|u(x)-U(x)|');

title('取不同步长时所得数值解的误差曲线')

hold off

function u=f_1(N)

%UNTITLED 两点边值问题求解

format long

h=1/N;

x=1/N*[0:N];

d=h^2./((1+x).^2);

d(1)=1;

d(N+1)=0.5;

alpha=[0,ones(1,N-1),0];

beta=-(2+h^2*(1-x)./((1+x).^2));

beta(1)=1;beta(N+1)=1;

gamma=[0,ones(1,N-1),0];

u=zeros(N+1,1);%数值解

u(1)=1;

g=zeros(N+1,1);w=zeros(N+1,1);

g(1)=d(1)/beta(1);w(1)=gamma(1)/beta(1);

for i=2:N

g(i)=(d(i)-alpha(i)*g(i-1))/(beta(i)-alpha(i)*w(i-1));

w(i)=gamma(i)/(beta(i)-alpha(i)*w(i-1));

end

g(N+1)=(d(N+1)-alpha(N+1)*g(N))/(beta(N+1)-alpha(N+1)*w(N));

u(N+1)=g(N+1);

for i=N:-1:2

u(i)=g(i)-w(i)*u(i+1);

end

end