拓扑排序

废了

另类排序顺序

Eg. 菜肴制作
要求在满足拓扑序的条件下，小编号的尽可能靠前。

小编号靠前 = 大编号靠后

不妨倒序考虑，先将大编号的向前放，最后倒序输出。

那么由于要让原本在后的在前，相当于反转拓扑序，所以建反图，然后满足大编号向前，即字典序越大越好，所以将队列改成大根堆即可。

数量关系建图

Eg. 数列恢复

有一个长度为 \(n\) 的整数数列 。

定义 \(s_{i, j} = \sum_{k = i}^j a_k\) 。

你现在只知道所有 \(s_{i, j}\) 的符号，请恢复一个合法的数列，或指出不存在这样的数列。

\(s_{i, j}\) 表示的是区间和，那么转化一下，可以用前缀和表示区间和 \(sum_j - sum_{i - 1} = s_{i, j}\)。

那么已知 \(s_{i, j}\) 符号，\(sum_j\) 和 \(sum_{i - 1}\) 的大小关系也就知道了。

通过大小关系建图，\(e_{u, v}\) 表示 \(sum_u < sum_v\)，然后拓扑排序构造 \(sum_v = \max(sum_u + 1)\) 即可。

那么 \(s_{i, j} = 0\) 呢？

既然 \(s_{i, j} = 0\) 表示 \(sum_{i - 1} = sum_j\) 那么不妨改变一下节点的定义：\(u\) 表示所有值为 \(sum_u\) 的点。当 \(s_{i, j} = 0\) 的时候 \(sum_{i - 1}\) 和 \(sum_j\) 等价，直接将其合并（用并查集维护起来），最后取值时直接取集合代表的值即可。

最后每个 \(a_i = sum_i - sum_{i - 1}\)。

丑陋代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100 + 10;
int n;
int f[N];
char s[N][N];
vector<int> G[N], g[N];
int find (int x) {
	if (x == f[x]) return x;
	return f[x] = find(f[x]);
}
int in[N], a[N];
map<int, int> mp;

signed main() {
	ios::sync_with_stdio(0);
	while (cin >> n) {
		mp.clear();
		for (int i = 0; i <= n; i ++) f[i] = i, G[i].clear(), g[i].clear(), a[i] = 0, in[i] = 0;
		for (int i = 1; i <= n; i ++) {
			for (int j = i; j <= n; j ++) {
				cin >> s[i][j];
				if (s[i][j] == '+') {
					G[i - 1].push_back(j);
				} else if (s[i][j] == '-') {
					G[j].push_back(i - 1);
				} else {
					f[find(j)] = find(i - 1);
				}
			}
		}
		for (int i = 0; i <= n; i ++) {
			for (auto u : G[i]) {
				g[find(i)].push_back(find(u)), in[find(u)] ++;
			}
		}
		queue<int> q;
		int tot = 0, idx = 0;
		for (int i = 0; i <= n; i ++) {
			if (!mp[find(i)]) {
				if (!in[find(i)]) q.push(find(i));
				idx ++;
				mp[find(i)] = 1;
			}
		}
		while (!q.empty()) {
			int u = q.front();
			q.pop(), tot ++;
			for (auto v : g[u]) {
				a[v] = max(a[v], a[u] + 1);
				if(!(-- in[v])) {
					q.push(v);
				}
			}
		}
		if(tot != idx) cout << "NO\n";
		else {
			cout << "YES\n";
			for (int i = 1; i <= n; i ++) {
				cout << a[find(i)] - a[find(i - 1 )] << ' ';
			}
			cout << endl;
		}
	
	}
	return 0;
}

最少路径覆盖问题

要求：简单路径，每条路径不能重复

由于欧拉路径是保证不重复经过每一条边的，所以可以尝试用欧拉路径去覆盖这张图。

若该图没有奇点，\(1\) 条欧拉路径即可覆盖完整个图。

若该图奇点数 \(\ge 2\)，那么该图会长这样：

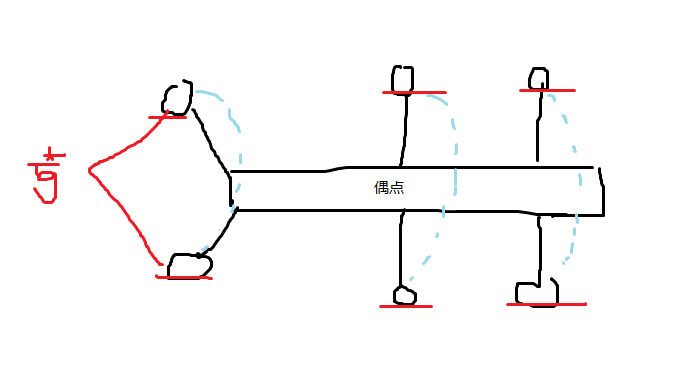
人类智慧

由于握手定理，奇点数量为偶数个。

若要使其被多条欧拉路径所覆盖，可以先将两两奇点连边，使得该图为欧拉图，然后找出该图的欧拉路径，删除其中的虚边，即为覆盖完该图需要的欧拉路径条数。

所以最后答案即为 : \(cnt / 2\)。

NKOJ P8436 守卫王国

#include <vector>
#include <iostream>
#include <stack>
#include <cstring>
using namespace std;
#define endl '\n'
const int N = 5e5 + 10;
int n, m;
struct edge {
	int to, nxt, id;
}e[N];
int h[N], idx, tmp;
void add (int u, int v, int id) {
	e[idx] = edge{v, h[u], id}, h[u] = idx, idx ++;
	e[idx] = edge{u, h[v], - id}, h[v] = idx, idx ++;
}
vector<int> col[N];
int bel[N], tot;
int vis[N];
void findltk (int u) {
	col[tot].push_back(u), bel[u] = tot;
	for (int i = h[u]; ~i ; i = e[i].nxt) {
		if(!bel[e[i].to]) findltk(e[i].to);
	}
}
int d[N];
bool mark[N];
stack<int> ans;
void dfs (int u) {
	for (int i = h[u]; ~i; i = e[i].nxt) {
		if(mark[i]) continue;
		h[u] = e[i].nxt;
		mark[i] = mark[i ^ 1] = 1;
		dfs(e[i].to);
		ans.push(e[i].id);
	}
}
signed main () {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	memset(h, -1, sizeof h);
	while(m --) {
		int u, v;
		cin >> u >> v;
		add(u, v, ++ tmp), d[u] ++, d[v] ++;
	}
	for (int i = 1; i <= n; i ++) {
		if(! bel[i]) ++ tot, findltk(i);
	}
	int num = 0;
	for (int i = 1; i <= tot; i ++) {
		int cnt = 0;
		if(col[i].size() == 1) continue;
		for (auto u : col[i]) {
			if(d[u] & 1) cnt ++;
		}
		num += max(cnt / 2, 1); // 一条链删除两个奇点 => ans >= sum(max(cnt / 2, 1))
		// 证明： 构造证明
	}
	cout << num << endl;
	for (int i = 1; i <= tot; i ++) {
		if(col[i].size() == 1) continue;
		int cnt = 0;
		vector<int> odd;
		for (auto u : col[i]) {
			if(d[u] & 1) cnt ++, odd.push_back(u);
		}
		if(cnt == 0) {
			dfs(col[i][0]);
			cout << ans.size() << ' ';
			while(!ans.empty()) cout << ans.top() << ' ', ans.pop();
			cout << endl;
		} else {
			for (int j = 0; j < odd.size(); j += 2) {
				if(cnt == 2) break;
				add(odd[j], odd[j + 1], 0);
				d[odd[j]] ++, d[odd[j + 1]] ++, cnt -= 2;
			}
			int st;
			for (auto u : col[i]) if(d[u] & 1) st = u;
			dfs(st);
			while(1) {
				vector<int> ve;
				while(!ans.empty() && ans.top() != 0) ve.push_back(ans.top()), ans.pop();
				cout << ve.size() << ' ';
				for (auto v : ve) cout << v << ' ';
				cout << endl;
				if(ans.size()) ans.pop();
				if(ans.empty()) break;
			}
		}
	}
	return 0;
}