1.快速排序

快速排序总结

原理

二分 + 分治

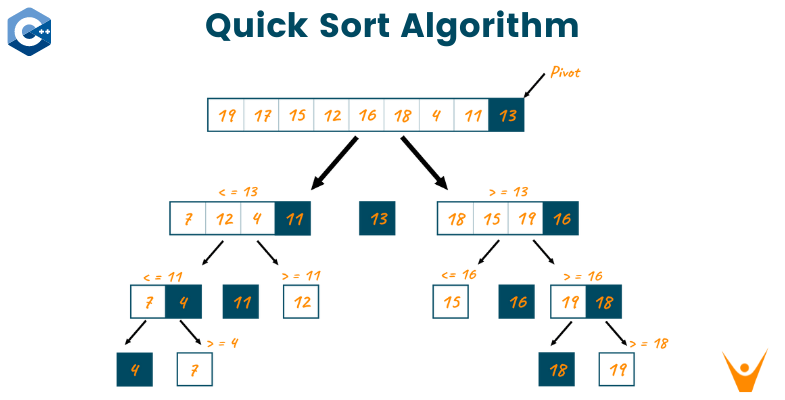
目标：

1. 选取基准值pivot
2. 根据基准值将数组一分为二，左边<= pivot， 右边 >= pivot
3. 根据pivot位置，将数组一份为二，递归排序处理

代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int s[N];

void quickSort(int l, int r){
    if(l >= r) return;
    int pivot = s[(l + r) >> 1];
    int i = l - 1, j = r + 1;
    while(i < j){
        do ++i; while(s[i] < pivot);
        do --j; while(s[j] > pivot);
        if(i < j) swap(s[i], s[j]);
    }
    quickSort(l, j);
    quickSort(j + 1, r);
}

int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n; i++) cin >> s[i];
    quickSort(0, n - 1);
    for(int i = 0; i < n; i++) cout << s[i] << " ";
    return 0;
}

接收输入数据格式如下，第一行是输入数据长度，第二行是具体数据，以空格分隔

4
3 1 2 4

Q&A

1. 为什么是先do后while？

while(i < j){
	do ++i; while(s[i] < pivot);
	do --j; while(s[j] > pivot);
	if(i < j) swap(s[i], s[j]);
}
能不能改成  
while(i < j){
	while(s[i] < pivot) ++i;
	while(s[j] > pivot) --j;
	if(i < j) swap(s[i], s[j]);
}

考虑如下情况

8 8 8

当值都相同时，i和 j会停止移动，导致死循环，先do后while能保证每轮循环指针都至少移动一格，从而跳出循环。

2. s[i]<pivot可以换成s[i]<=pivot吗？

不能，考虑如下输入

8 8 8

使用<=，i会不停地增长，根本没有条件使其停下来。所以不能换。

2. 划分区间时，能将j换成i吗？

即，将

quickSort(l, j);
quickSort(j + 1, r);

改成

quickSort(l, i);
quickSort(i + 1, r);

答：不能

在快排中，每层递归，都需要将数据划分成的两个子数组，且左边<= pivot， 右边 >= pivot --条件1

在每一轮运行结束时，各位置有如下含义：

• i >= j

• s[i] >= pivot, s[j] <= pivot

• s[l..i-1] <= pivot

• s[j+1...r] >= pivot

所以 s[l,j] <= pivot、s[j+1,r] >= pivot，满足 条件1，划分合理

但 s[i] >= pivot，所以 s[l,i]并不满足<= pivot，虽然 s[i+1,r] >= pivot成立，但还是不满足 条件1，所以不能使用i进行划分

3. 那如何使用i进行区间划分？

可以划分为 [l, i-1]和 [i, r]，此时就满足条件1了

同时需要将pivot的求法改为

int pivot = s[(l+r+1)>>1];

为什么？先看下出错案例：

输入：
2
1 2

算法模拟：
# 第一轮
	下标：[0,1] 
		pivot = 0
		执行结束时：i = 0, j = 0
		划分为[0,-1]和[0,1]
# 第二轮，左边子数组
  [0,-1], 返回不执行
# 第二轮，右边子数组
	[0,1]
	下标和起始状态一样，显然之后会陷入死循环

死循环的原因：

当数组有序，且l和r相差较小时，pivot=s[(l+r)>>1]=s[l]（比如上面的例子）

于是起始状态为：i=l-1, j=r+1, pivot=s[l]

• 更新i：i移动一次等于l，此时s[l]=pivot，停止更新
• 更新j：因为有序，j会一直减到pivot所在的位置s[l]，此时j=l
• 此时i = j，退出循环，此时i=j=l

于是子数组 [l, i-1]和 [i, r]，就变成了 [l, l-1]和 [l, r]，从而陷入死循环

解决方法：保证i!=l，即pivot不能等于l

而 (l+r+1)>>1是向上取整，l和r再接近， 求出来结果也等于r，避免了pivot取到l

以r分割也是同理，当数组有序，且数组较小时，pivot=s[(l+r+1)>>1]=r，此时i和j会都移动到r

[l, j]和 [j+1, r]就等于 [l, r]和 [r+1, r]，从而陷入死循环

解决方法就是保证j!=r，即pivot不能等于r

而 int pivot = (l+r)>>1是向下取整，此时 pivot = l，避免了pivot取到r

4.总结

在快排中，每层递归，都需要将数据划分成的两个子数组，且左边<= pivot， 右边 >= pivot --条件1

在每一轮运行结束时，各位置有如下含义：

• j <= i

• s[i] >= pivot, s[j] <= pivot

• s[l..i-1] <= pivot

• s[j+1...r] >= pivot

为满足条件1

• 以i划分，区间可为[l,i-1]和[i,r]
• 以j划分，区间可为[l,j]和[j+1,r]

又为了防止下标停止更新，陷入死循环，

即[i,r]不能取到[l,r]，[l,j]不能取到[l,r]

即以i划分，pivot不能取到l，以j划分，pivot不能取到r

因此

• 以i划分，pivot向上取整：int pivot = s[(l+r+1)>>1]

• 以j划分，pivot向下取整：int pivot = s[(l+r)>>1]

注

二分算法也有同样的边界问题，解决思路也相同。