Title

二分查找

 

 

 

1. 作用和要求

当我们要从一个序列中查找一个元素的时候，二分查找是一种非常快速的查找算法，二分查找又叫折半查找。它对要查找的序列有两个要求，一是该序列必须是有序的（即该序列中的所有元素都是按照大小关系排好序的，升序和降序都可以，本文假设是升序排列的），二是该序列必须是顺序存储的。图1展示的就是一个能进行二分查找的序列。

图1 有序且顺序存储的序列

如果一个序列是无序的或者是链表，那么该序列就不能进行二分查找。之所以被查找的序列要满足这样的条件，是由二分查找算法的原理决定的。

2. 算法原理

二分查找算法的原理如下：

1. 如果待查序列为空，那么就返回-1，并退出算法；这表示查找不到目标元素。

2. 如果待查序列不为空，则将它的中间元素与要查找的目标元素进行匹配，看它们是否相等。

3. 如果相等，则返回该中间元素的索引，并退出算法；此时就查找成功了。

4. 如果不相等，就再比较这两个元素的大小。

5. 如果该中间元素大于目标元素，那么就将当前序列的前半部分作为新的待查序列；这是因为后半部分的所有元素都大于目标元素，它们全都被排除了。

6. 如果该中间元素小于目标元素，那么就将当前序列的后半部分作为新的待查序列；这是因为前半部分的所有元素都小于目标元素，它们全都被排除了。

7. 在新的待查序列上重新开始第1步的工作。

二分查找之所以快速，是因为它在匹配不成功的时候，每次都能排除剩余元素中一半的元素。因此可能包含目标元素的有效范围就收缩得很快，而不像顺序查找那样，每次仅能排除一个元素。

3. 示例

我们用两个示例来演示二分查找的过程，一看就能明白。第一个示例演示查找成功的情况，第二个示例演示查找不到目标元素的情况。

演示过程中用到的变量如下：low指向待查序列中的第一个元素，high指向待查序列中的最后一个元素，mid指向待查序列的中间元素，target代表要查找的目标元素。

3.1 查找成功的情况

假设原始序列为array=[3, 12, 24, 31, 46, 48, 52, 66, 69, 79, 82]，目标元素target=52。

1. 开始时，low=0，high=10，mid=(low + high) / 2 = 5。

比较中间元素和目标元素，48小于52。这说明若目标元素存在，则它必定在原序列的后半部分。让low=mid + 1 = 6而high不变，这样low和high就指向了原序列的后半部分。

2. 此时，low=6，high=10，mid=(low + high) / 2 = 8。

同样的，比较新的中间元素和目标元素，69大于52。这说明若目标元素存在，它必定在当前待查序列的前半部分。让high=mid - 1 = 7而low不变，这样low和high就指向当前待查序列的前半部分。

3. 此时，low=6，high=7，mid=(low + high) / 2 = 6。

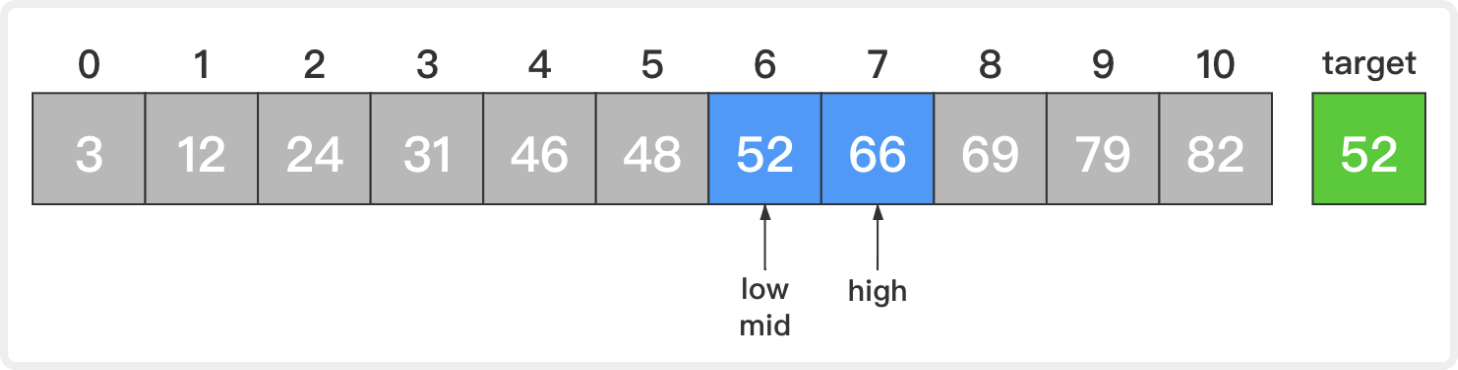
比较新的中间元素和目标元素，52等于52。查找成功，返回该中间元素的索引6并退出算法。

3.2 查找不到的情况

假设原始序列为array=[5, 10, 22, 29, 43, 57, 58, 61, 73, 77, 81]，目标元素target=70。

1. 开始时，low=0，high=10，mid=(low + high) / 2 = 5；

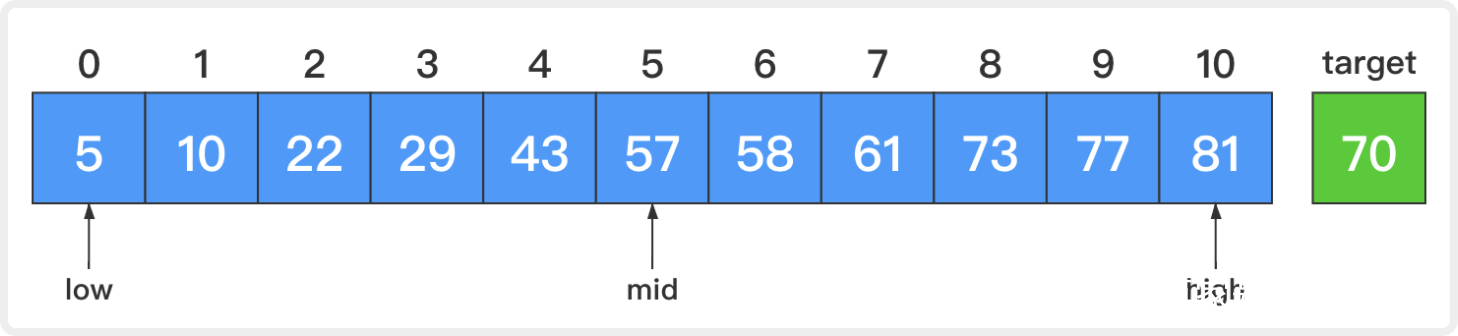
比较中间元素和目标元素，57小于70。这说明若目标元素存在，那么它一定在原序列的后半部分。让low=mid + 1 = 6而high不变，这样low和high就指向原序列的后半部分。

2. 此时，low=6，high=10，mid=(low + high) / 2 = 8；

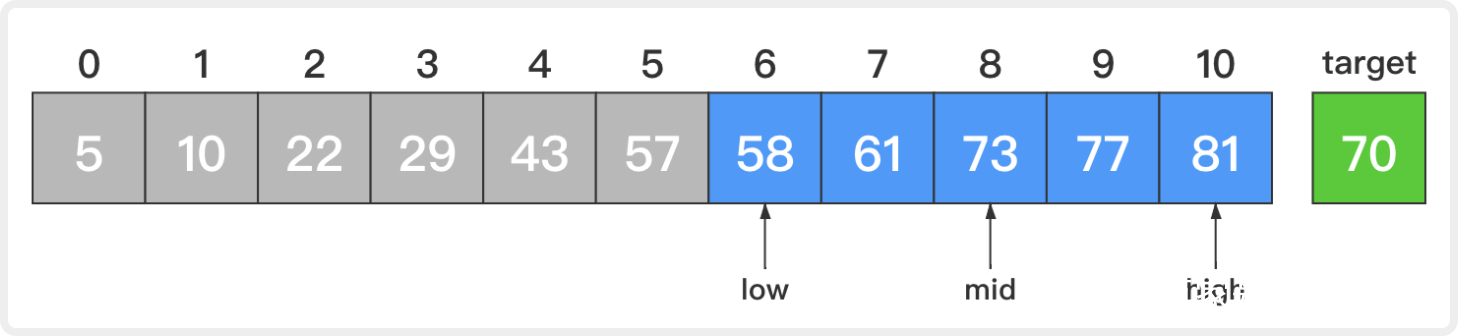
比较新的中间元素和目标元素，73大于70。这说明若目标元素存在，那么它一定在当前待查序列的前半部分。让high=mid - 1 = 7而low不变，这样low和high就指向当前待查序列的前半部分。

3. 此时，low=6，high=7，mid=(low + high) / 2 = 6；

比较新的中间元素和目标元素，58小于70。这说明若目标元素存在，那么它一定在当前待查序列的后半部分。让low=mid + 1 = 7而high不变，这样low和high就指向当前待查序列的后半部分。

4. 此时，low=7，high=7，mid=(low + high) / 2 = 7；

比较新的中间元素和目标元素，61小于70。这说明若目标元素存在，那么它一定在当前待查序列的后半部分。让low=mid + 1 = 8而high不变。

5. 此时，low=8，high=7，low大于high说明待查序列已为空，也就说明查找不到目标元素。此时，返回-1并退出算法，表示查找不成功；

4. 算法实现

 1 /*** 
 2  * @Description: one new start!
 3  * @version: 
 4  * @Author: MocWangYu
 5  * @Date: 2020-10-27 11:05:45
 6  * @LastEditors: MocWangYu
 7  * @LastEditTime: 2020-10-27 12:10:46
 8  */
 9 #include<iostream>
10 using namespace std;
11 
12 int BinSearch(int a[],int low,int high,int k){
13     int mid;
14     if(low<=high)
15     {
16         mid=(low+high)/2;
17         if(a[mid]==k)
18             return mid;
19         if(a[mid]>k)
20             return BinSearch(a,low,mid-1,k);
21         else
22         {
23             return BinSearch(a,mid+1,high,k);
24         }
25     }else
26     {
27         return -1;
28     }
29     
30 }
31 int main(){
32     int i,k;
33     cout<<"输入查找的数：";
34     cin>>k;
35     int a[]={3,12,24,31,46,48,52,66,69,79,82};
36     int n=sizeof(a)/sizeof(a[0]);
37     i=BinSearch(a,0,n-1,k);
38     if(i>=0)
39         cout<<"a["<<i<<"]="<<k<<endl;
40     else
41         {
42             cout<<"未找到"<<k<<"元素"<<endl;
43         }
44             
45     return 0;
46 }

 

posted @ 2020-10-29 12:11  WAASSTT  阅读(250)  评论(0)    收藏  举报
Title