CUDA编程模型——组织并行线程2 （1D grid 1D block）

在”组织并行编程1“中，通过组织并行线程为”2D grid 2D block“对矩阵求和，在本文中通过组织为 1D grid 1D block进行矩阵求和。一维网格和一维线程块的结构如下图：

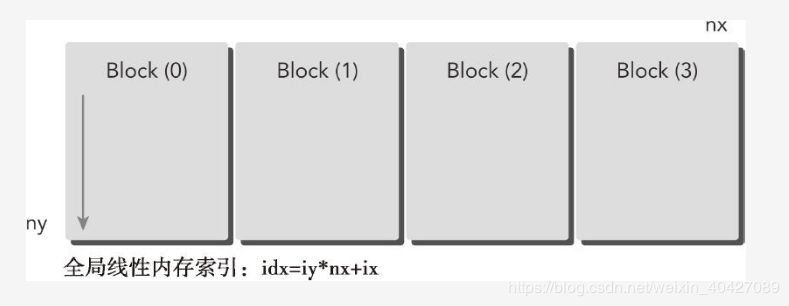
其中，nx是x方向上的最大线程数，ny是一个线程需要处理的数据元素的个数（因为块是一维的，照理应该没有ny）。所以这里这里只有ix是对线程的真正索引，iy是线程内部数据的索引（这个时候要把线程看成一个主线程，里面有ny个子线程组成的，每个子线程依次处理一个数据。但一定要记住，这个子线程实际上并不存在，是并行里面的串行）。这样每个数据的索引 idx 依然满足idx=iy*nx+ix；其中iy是从0迭代到ny的。

相应的核函数如下：（如果核函数和2Dgrid2Dblock一样，会怎样？）

 1 __global__ void sumMatrixOnGPU1D(float *MatA,float *MatB,float *MatC,int nx,int ny)
 2 {
 3     unsigned int ix=threadIdx.x+blockIdx.x*blockDim.x;//获得x方向上的网格坐标
 4     if(ix<nx)//防止越界
 5     {
 6         //从这里开始，就已经是线程里面的串行了
 7         for(int iy=0;iy<ny;i++)
 8         {
 9             int idx=iy*nx+ix;//得到计算矩阵的坐标idx
10             C[idx]=A[idx]+B[idx];
11         }
12     }
13 }

一维网格和块的线程配置：

1 dim3 block(32,1);
2 dim3 grid((block.x-1)/block.x+1,1);

使用以下配置调用核函数：

1 sumMatrixOnGPU1D <<< grid, block >>>(d_MatA, d_MatB, dMatC, nx, ny);

设置矩阵数据量的大小为：

1 // set up data size of matrix
2  int nx = 1 << 14;
3  int ny = 1 << 14;

运行结果如下所示：(可以到一维网格一维线程块实际分配的线程数是：32*512=16384）

接着按照如下增加线程块的大小：

1 dim3 block(128,1);
2 dim3 grid((block.x-1)/block.x+1,1);

运行结果如下：

可以看出核函数运行的更快了。

主要参考文献：

《 CUDA C编程权威指南》
https://blog.csdn.net/weixin_40427089/article/details/86696707

posted on 2019-03-31 21:27 IMWH 阅读(506) 评论(0) 收藏举报