矩阵优化dp

关于能用矩阵乘法优化的DP题目，有如下几个要求：

1. 转移式只有加法，清零，减法etc.，max和min运算不允许【符合矩阵的计算规律】
2. 转移式中关于前几位dp结果得到的系数必须是常量【和常数项矩阵进行相乘】
3. 转移次数一般超级多【运用快速幂转化成mod】
4. 由于转移次数多，一般都要模一个int范围内的数【ksm当然要约数啦】

矩阵的原理：

 

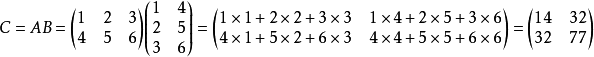
 n*m的矩阵，若n=m为方阵，单位矩阵：对角线为1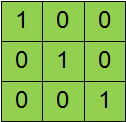

 

 

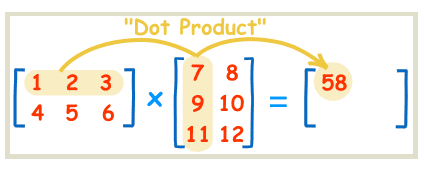
矩阵乘法中第一个矩阵的列要等于第二个矩阵的行

一个m∗n的的A矩阵，和一个n∗p的B矩阵相乘，将得到一个m∗p的矩阵C 

 

 

 

 

 

 

 

 对于矩阵的乘法，我们有以下的优化方式（分块优化 暂且不使用）

 

 

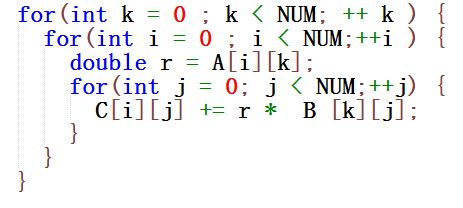
但是，矩阵乘法有结合律。

A*B*C=A*(B*C)

这是一个最常用的运算律，使之可以用矩阵快速幂。

3.构造技巧。

矩阵乘法主要用途还是矩阵加速dp。

例如什么n=1e9之类的。

关键还是在于列出dp或者叫递推式子。

BY LYD：

1.一定是线性递推式（斐波那契数列）

2.总有一个转移矩阵（通常还是正方形）一直不变（才能快速幂）//(就比如漫步校园那一个dp)

3.矩阵边长不能太大，因为乘法复杂度是O(n^3)

4.矩阵保留能往下递推的项即可。