数学 同余问题
1.扩展欧几里得算法:
- 求解问题a,b,qcd(a,b)=d;扩展欧几里得算法就是求出这么一组解ax+by=d
![]()
推导过程
- 如果求出来易祖杰x0,y0,那么通解x=x0+k*【a/d】 y=y0-k*[b/d]k整数就可
- 通常形式ax同余b(mod c)
- 那么就转化成ax+cy=b
T1求解线性同余方程 ax同余1(mod b) 转化为 ax+by=1,就可以了
- 注意求最小正余数的套路(x%b+b)%b;
- exgcd的返回值是gcd要注意
- 写成exgcd(b,a%b,y,x)y-=a/b*x更好些
- 代码如下:
-
![]() View Code
View Code#include <stdio.h> #include <algorithm> #include <cstring> using namespace std; typedef long long ll; int exgcd(int a,int b,int &x,int& y) { if(b==0) { x=1,y=0; return a; } int d=exgcd(b,a%b,y,x);//继续递归 y-=a/b*x; return d; } int main() { int a,b; scanf("%d%d",&a,&b); int x,y; exgcd(a,b,x,y); printf("%d",(x%b+b)%b); return 0; }
如果中间会爆int的话,就需要ll就可以了

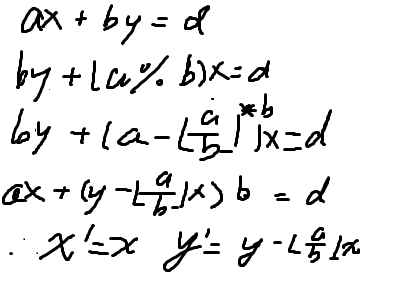



 浙公网安备 33010602011771号
浙公网安备 33010602011771号