P2257 莫比乌斯反演 gcd相关

这是第一道莫比乌斯的题目，所以分析的细致一点（w）

1.经典问题：求解gcd(x,y)=1,也就是互质的x,y组数有多少组(x 1,n, y 1,m)

 

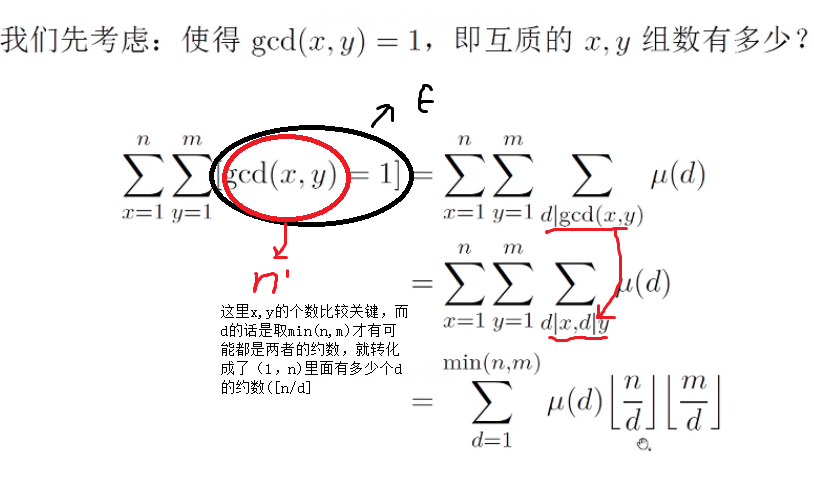
 那么我们就可以回到原来的题目（也就是将一二维求和直接转化为数）

预处理μ以及前缀和，按照[n/d][m/d]的取值范围分段，会分成跟下n个区间，段点的个数是好的

套路：莫比乌斯反演。交换求和顺序

 

 

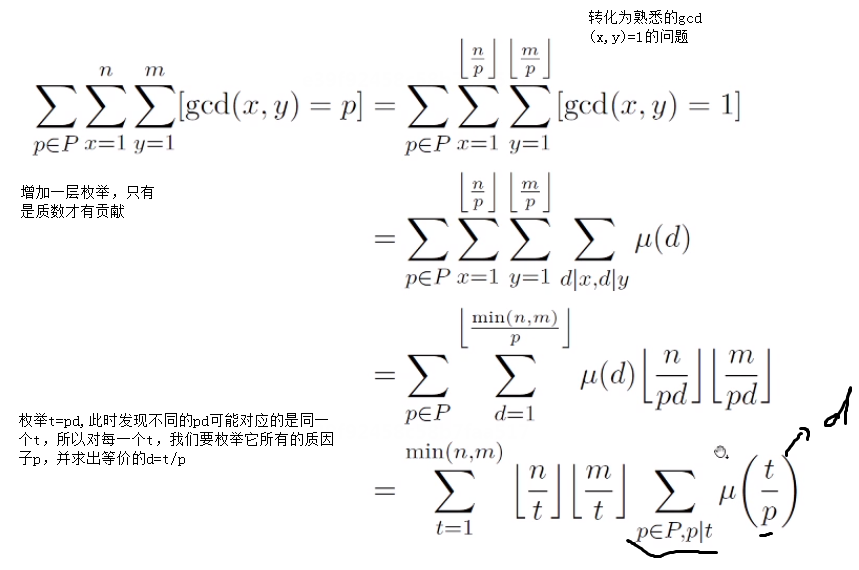
 接下来见代码：

#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <cctype>

using namespace std;
typedef long long ll;
const int maxn=10000020;

int read()
{
    int x=0,b=1;char c=getchar();
    while(!isdigit(c)) b=c=='-'?-1:1,c=getchar();
    while(isdigit(c)) x=x*10+c-'0',c=getchar();
    return x*b;
}
int prime[maxn],mu[maxn],g[maxn],vis[maxn],cnt=0;
ll sum[maxn];

void getmu(int maxx)
{
    mu[1]=1;
    for(int i=2;i<=maxx;i++)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<cnt,i*prime[j]<=maxx;j++)
        {
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) break;
            else mu[i*prime[j]]=-mu[i];
        }
    }
    for(int j=0;j<cnt;j++)
        for(int i=1;i*prime[j]<=maxx;i++)
        g[i*prime[j]]+=mu[i];//自底而上，相当于说枚举了在n以内的所有质因子的倍数，这样子就相当于对于每一个n，枚举有可能整除它的质因子//这一点非常重要，要注意理解 
        //关键要看式子，他要求的是对于每一个i(1-n)，对于可以整除他的质数p，μ(d)的和，那么不妨转化成枚举每一个质数p，计算每一个质数对于在n当中的所有的倍数的贡献就可以了 
    for(int i=1;i<=maxx;i++) sum[i]=sum[i-1]+(long long)g[i];
}
int main()
{
    int t;t=read();
    getmu(10000000);
    //for(int i=1;i<=10;i++) printf("%d ",sum[i]);
    while(t--)
    {
        int n,m;n=read();m=read();
        if(n>m) swap(n,m);ll ans=0;
        for(int l=1,r;l<=n;l=r+1)//再次强调一下分块，公式 n/(n/l)是每一块当中右端点的临界点，所以下一个l就是r+1
        {//因为我们推导到需要特殊点n/l所以我们才会使用分块把两个特殊点值相同的合并计算，并且如果有一个要更新就得跳一步 
            r=min(n/(n/l),m/(m/l));
            ans+=(1ll)*(n/l)*(m/l)*(sum[r]-sum[l-1]);
        }
        printf("%lld\n",ans);
    }
} 

然后，关于莫比乌斯的相关文章：https://www.luogu.com.cn/blog/An-Amazing-Blog/mu-bi-wu-si-fan-yan-ji-ge-ji-miao-di-dong-xi

https://www.cnblogs.com/peng-ym/p/8647856.html

这两个就已经足够用了

总结一下：这是一道gcd类型的莫比乌斯反演题，由此我们可以得出来几个套路模式

这也就是非常经典的e=1*μ的狄利克雷卷积

 

 这是较为基础的推导，之后的话我们还是需要设置函数老老实实莫比乌斯反演。具体如下

 

 3.关于化简：我们在推式子的时候的最终目的是减少枚举层数和化简式子，让他变成我们更容易处理的形式和方法，且我们的原则就是变量能少就尽可能的少

 

 原则上来看枚举dp是两个变量，这显然是不明智的，所以我们把它转化成t这一个变量，在求解过程中直接利用前缀和来计算就可以了（通过结构优化的角度同样可以想到如果要前缀和的话，那两个东西都必须要干掉）