从1开始的数论 2

整除分块

1.对于我们之前介绍过的特殊点 [n/d]我们可以发现，在一道完整的序列上，其中每一段连续的块上的特殊点的值是相等的，换而言之，他是按照块状分布的

2.通过打表之类的各种方法,我们惊喜的发现对于每一个值相同的块，它的最后一个数就是n/(n/i)n/(n/i)。得出这个结论后，我们就可以做的O(n−−√)O(n)处理了。

假设我们需要求的是Σ（1-n） [n/i]

那么我们可以得到如下的代码

#include <stdio.h>

using namespace std;

int n,ans=0;

int main()
{
    scanf("%d", &n);
    for(int l = 1, r;l <= n; l = r + 1)
    {
        r=n/(n/l);printf("%d ", r);
        ans+=(r-l+1)*(n/l);
    }
    printf("\n%d",ans);
    return 0;
}

以10为例，分界点就是1 2 3 5 10；

 

题目 3：求无平方因子数的个数

对于积性函数我们不妨来总结一下：

常见积性函数

1. μ(n)μ(n)——莫比乌斯函数。关于这个函数，我在莫比乌斯反演中说的挺清楚的了(233)，(PS：不过我将会在下文中，从另一种角度介绍它的性质。也算是把坑给填完吧)
2. φ(n)φ(n)——欧拉函数。表示不大于nn且与nn互质的正整数个数，十分常见的数论函数。用数学式子表示即：φ(n)=∑ni=1[(n,i)=1]φ(n)=∑i=1n[(n,i)=1] (PS:(n,i)(n,i)表示gcd(n,i)gcd(n,i))
3. d(n)d(n)——约数个数。表示nn的约数的个数。用式子表示为：d(n)=∑d|n1d(n)=∑d|n1，也可以写作：d(n)=∑nd=1[d|n]d(n)=∑d=1n[d|n] （其实没什么太大区别啦！）
4. σ(n)σ(n)——约数和函数。 即nn的各个约数之和。表示为：σ(n)=∑d|nd=∑nd=1[d|n]⋅dσ(n)=∑d|nd=∑d=1n[d|n]⋅d

(PS：接下来列举的是完全积性函数)
(PS：代表字母可能会与他人的略有不同，似乎在数学中没有统一的字母)

1. ϵ(n)ϵ(n)——元函数。似乎也有人把它叫作e(n)e(n)？其实无所谓啦~~我们只需要知道ϵ(n)=[n=1]ϵ(n)=[n=1]。(看到这个是不是有种莫名的熟悉感呢？到了下文中，就会发现这种熟悉感是从哪来的啦！)
2. I(n)I(n)——恒等函数。所谓恒等就是这个函数的值恒为11。
3. id(n)id(n)——单位函数。id(n)=nid(n)=n

【PS：注意欧拉和mobiwus的特殊性质】

13.杜教筛

PS：特别要记住一点：积性函数有一个特别重要的性质，那就是（积性函数∗∗积性函数）仍然为积性函数！！！这个性质可以用来判断能否被杜教筛

• 杜教筛是以低于线性的时间复杂度来计算积性函数的前缀和的神奇筛法！

下面对杜教筛的推导过程进行一下说明：

 

 

 

 

利用狄利克雷卷积来构造递推式，对一些数论的函数进行快速的求和（平常的算法就是使用线性筛法来O（n）
1.求Σ（1-n）φ(n) 因为有欧拉函数 自然考虑 id = φ * 1；

我们来进行一下推导  假设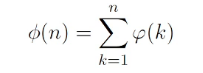

 

 然后 因为id=n，我们自然联想到自然数的求和 =

 

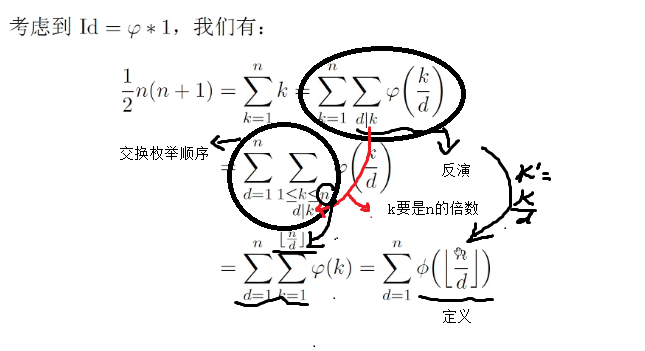
接下来 ，我们就要在结果当中寻找我们需要的东西

 

 

 

后面那个东西是子问题，可以递归解决【跟斐波那契一样，我们需要使用记忆化实现，计算特殊点处的函数值】

3.时间复杂度：特殊点的结构是在（1-跟n和跟n到n两个之间）

 

 

 

欧拉定理

• 对于正整数n以及和他互质的正整数a，我们有：a^φ(n)≡1（mod n）(补充说明，只有在OI中，互质还可以使用 a⊥b来表示）
• 常用结论：如果a和n满足gcd（a,n）=1,那么就有 a^m≡a^m%φ(n)(mod n)