【水题】【计算几何】GYM103483H_Lots of Parabolas

题目链接：https://codeforces.com/gym/103483/problem/H

题意：给 $n$ 个抛物线，对于 $a>0$ 的抛物线 $i$，取点集 $S_i = \{(x,y)|y>ax^2+bx+c\}$，对于 $a<0$ 的抛物线 $j$，取点集 $S_j = \{(x,y)|y<ax^2+bx+c\}$，取 $S=\cup S_i$，输出 $S$ 中的任意一个元素（保证 $S \neq \emptyset$）。

 

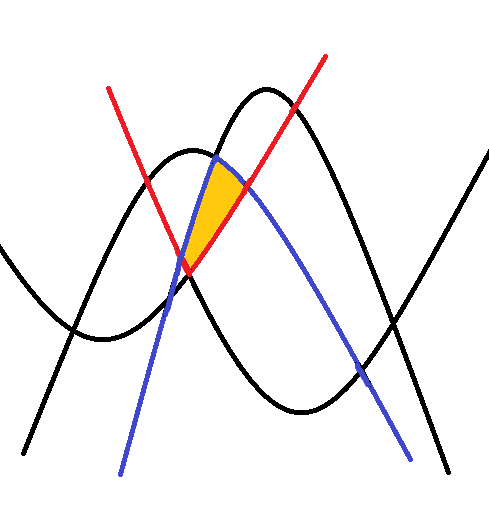
思路：把 $a>0$ 的抛物线放到集合 $M$ 中，把 $a<0$ 的抛物线放到集合 $N$ 中，构造函数 $Up(x)=Max(M_i(x)) ，Down(x)=Min(N_i(x))$，如下图中红线和蓝线。在红蓝两线之间的橙色块，即符合 $G(x)=Up(x)-Down(x)<0$的点集，就是符合条件的点的点集。又因为 $G(x)$ 是 $Convex$ 的函数，所以二分答案即可，检查时每次遍历所有抛物线找到对应 $x$ 的 $G(x)$ 的导数，导数为正数就往左找，导数为负数就往右找。（注意特判一下 $M$ 或 $N$ 为空集的情况）

代码：

#include <bits/stdc++.h>
//#include <windows.h>
#define index xedni
#define bug cout<<"bug "<<__LINE__<<endl
const int MOD=1e9+7;
const int inf=1e9+7;
//const int MAXN=;
using namespace std;
struct Curv
{
	long double a,b,c;
}; vector<Curv> Up,Down;
int n;
inline long double Tan(Curv C,long double k)
{
	long double a=C.a,b=C.b;
	return (long double)2.0*a*k+b;
}
inline long double Calc(Curv C,long double k)
{
	long double a=C.a,b=C.b,c=C.c;
	return (long double)a*k*k+b*k+c;
}
bool Check(long double k)
{
	int idup,iddown;
	long double MAX=-1e18,MIN=1e18;
	for(int i=0;i<(int)Up.size();i++)
	{
		long double res=Calc(Up[i],k);
		if(res>MAX) MAX=res,idup=i;
	}
	for(int i=0;i<(int)Down.size();i++)
	{
		long double res=Calc(Down[i],k);
		if(res<MIN) MIN=res,iddown=i;
	}
	return (Tan(Up[idup],k)-Tan(Down[iddown],k))>0.0;
}
signed main()
{
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
	cin.tie(0); cout.tie(0);
	ios_base::sync_with_stdio(false);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		long double a,b,c; scanf("%llf%llf%llf",&a,&b,&c);
		a+=(long double)0.0,b+=(long double)0.0,c+=(long double)0.0;
		if(a>0.0) Up.push_back({a,b,c});
		else Down.push_back({a,b,c});
	}
	if(Up.empty()) { cout<<"0.0 -1000000000000000000000"<<endl; return 0; }
	if(Down.empty()) { cout<<"0.0 1000000000000000000000"<<endl; return 0; }
	long double l=(long double)-1e18,r=(long double)1e18;
	for(int T=1;T<=100;T++)
	{
		long double mid=(l+r)/2;
		if(Check(mid)) r=mid;
		else l=mid;
	}
	long double UpLim=(long double)-1e18,DownLim=(long double)1e18;
	for(int i=0;i<(int)Up.size();i++)
	{
		long double res=Calc(Up[i],l);
		if(UpLim<res) UpLim=res;
	}
	for(int i=0;i<(int)Down.size();i++)
	{
		long double res=Calc(Down[i],l);
		if(DownLim>res) DownLim=res;
	}
	cout<<fixed<<setprecision(15)<<l<<" ";
	cout<<fixed<<setprecision(15)<<(UpLim+DownLim)/(long double)2.0<<endl;
	return 0;
}