线段树

线段树是我们平时接触的最多的数据结构了吧，应该没有之一。~~对我来说是这样的。~~
对于这种数据结构，他拥有比树状数组更优秀的延展性。如果说树状数组就是个连区间求和都干不了的东西，那么线段树就是一个能支持众多区间问题的神器了。
来说说几个比较有趣的东西。

单点加，区间查。这个东西也算有意思吧？
区间加，区间查。这个东西就是在上面的东西上加一个懒惰标记，维持时间复杂度。
区间加，区间合并某种信息。比如非常厉害的小白逛公园。这种就是在线段树的节点上维护三个东西：从左起连续一段的某个信息，然后区间中的某些信息，然后从右边起连续一段的某个区间。合并的时候就是左节点的右边一段连续信息拼上右节点的左边连续一段信息作为新节点的中间一段，然后这一个节点的左边连续一段信息继承左节点的信息，右边连续一段同理。这样就能维护最大子区间或者像树的直径这种可以合并的东西。说到合并，线段树也支持维护倍增，具体可以看倍增的一道题。
权值线段树。这个东西是开在权值上的线段树，一般伴随着离散化。同时线段树上维护的一般是权值出现次数。
动态开点线段树。这个东西一般是开在权值上的。毕竟谁没事会把下标开那么大以至于需要动态开点呢。动态开点就是发现线段树本来一次开满了空间消耗大，而且用不了多少。所以动态开点就是做到点有各用。没用的是不会开的。
主席树。这个是权值线段树+动态开点。因为主席树需要维护每一个历史版本，鉴于空间，我们选择需要就开，非必要不开的原则。至于主席树别的啥的，可以看我的博客。
线段树的合并。非常类似于 FHQ 的合并。只不过这是线段树的合并，都是差不多的。
扫描线，二位数点。线段树是可以做更复杂的扫描线题目的，完美吊打树状数组。

逆序对

这道题就是一道二位数点的题了。但是二位数点树状数组能做，为什么线段树不能呢？树状数组只不过是线段树的简化产物。
代码就不放了，感觉是个 OIer 就能写。

P2880 [USACO07JAN] Balanced Lineup G

开两个线段树，一个存最大值一个村最小值即可。

P1198 [JSOI2008] 最大数

边修改边查询不就行了。
当然也可以动态维护 ST 表。

P3660 [USACO17FEB] Why Did the Cow Cross the Road III G

像这种题不是可以莫队秒吗？
但是讲讲正常的线段树做法。
简化一下题面就是在一段区间内（这个区间的两端颜色相等），有多少个数只出现了一次。
我们采用HH的项链做法。我们先按照左端点排序，我们发现有用的只有出现两次中的较后者。毕竟他们是统计总对数，不是统计每一个数它能产生多少贡献。所以我们每一次更新时只需要把 \(r\) 更新进线段树即可。答案的更新就是 \(query(s[i].r-1)-query(s[i].l)\)。
由于这是一道我好久之前写的题，所以依然保留树状数组。

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int N=1e5+5;
struct node
{
	int l,r;
	node(){l=r=-1;}
	friend bool operator<(const node &x,const node &y)
	{
		return x.l<y.l;
	}
}q[N<<1];
int n,ans;
struct BIT
{
	int T[N];
	int lb(int x){return x&-x;}
	void upd(int x)
	{
		for(;x<=n*2;x+=lb(x))
			T[x]++;
	}
	int query(int x)
	{
		int res=0;
		for(;x;x-=lb(x))
			res+=T[x];
		return res;
	}
}T;
int main()
{
	cin>>n;
	for(int i=1,x;i<=n*2;i++)
	{
		cin>>x;
		if(q[x].l==-1) q[x].l=i;
		else q[x].r=i;
	}
	sort(q+1,q+1+n);
	for(int i=1;i<=n;i++)
		T.upd(q[i].r),ans+=T.query(q[i].r-1)-T.query(q[i].l);
	cout<<ans;
	return 0;
}

P2574 XOR的艺术

发现是异或，所以开一个异或懒标记不就行了。

P4198 楼房重建

a good 题目。
发现是个单点修改区间查询，考虑线段树。
关键的问题是怎么 pushup。
我们考虑修改的这一个楼层的高度（实际是斜率，我们说的通俗一点）。我们发现我们只需要递归的更新被修改的那一半即可。
我们可以先找到这个被修改的值得下标，并且当前这个点的值为 \(h\)，也就是修改后是 \(h\)，然后这个区间分为 \(l\)，\(r\) 两部分。\

如果 \(l\) 的最大值小于等于现在的 \(h\)，那么这个时候 \(l\) 的部分就不可能有任何贡献了，就去递归 \(l\) 即可。因为从斜率的视角来看，这样有个大斜率的东西横在后边，那 \(r\) 还怎么跟 \(l\) 产生贡献。
否则我们就先去递归 \(l\) 部分，然后加上 \(r\) 对 \(l\) 的贡献即可。这个贡献就是 \(r\) 部分最长不上升子序列了。这个就是 \(len_x-len_{l}\)，注意不是 \(len_{r}\)，原因很简单，就是因为在 \(len_{r}\) 的数不一定全被选进 \(len_x\)。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m;
double a[N];
struct segmant {
	double val[N << 2];
	int len[N << 2];
	int push_up(int u, int l, int r, double x) {
		if (val[u] <= x) return 0;
		if (a[l] > x) return len[u];
		if (l == r) return a[l] > x;
		int mid = (l + r) >> 1;
		if (val[u << 1] <= x) return push_up(u << 1 | 1, mid + 1, r, x);
		return push_up(u << 1, l, mid, x) + len[u]-len[u<<1];
	}
	void change(int l, int r, int pos, int x, int u) {
		if (l == r) {
			val[u] = 1.0 * x / pos;
			len[u] = 1;
			return ;
		}
		int mid = (l + r) >> 1;
		if (pos <= mid) change(l, mid, pos, x, u << 1);
		else change(mid + 1, r, pos, x, u << 1 | 1);
		val[u] = max(val[u << 1], val[u << 1 | 1]);
		len[u] = len[u << 1] + push_up(u << 1 | 1, mid + 1, r, val[u << 1]);
	}
} tree;
int main() {
	cin >> n >> m;
	while (m--) {
		int pos, x;
		cin >> pos >> x;
		a[pos] = 1.0 * x / pos;
		tree.change(1, n, pos, x, 1);
		cout << tree.len[1] << endl;
	}
	return 0;
}

P3224 [HNOI2012] 永无乡

左右节点的权值线段树合并即可。可以看成一个板子题。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,a[N],rt[N],f[N];
struct SGT
{
	int cnt;
	struct node
	{
		int l,r,sm,L,R;
	}t[N<<5];
	SGT(){cnt=0;}
	int upd(int l,int r,int x)
	{
		int id=++cnt;t[id].sm++;
		t[id].L=l,t[id].R=r;
		if(l==r) return id;
		int mid=(l+r)>>1;
		if(x<=mid) t[id].l=upd(l,mid,x);
		else t[id].r=upd(mid+1,r,x);
		return id;
	}
	int merge(int u,int v,int l,int r)//类似于平衡树
	{
		if(!u||!v) return u|v;
		int id=++cnt,mid=(l+r)>>1;
		t[id].sm=t[u].sm+t[v].sm,t[id].L=l,t[id].R=r;
		t[id].l=merge(t[u].l,t[v].l,l,mid);
		t[id].r=merge(t[u].r,t[v].r,mid+1,r);
		return id;
	}
	int query(int x,int k)
	{
		if(k>t[x].sm) return -1;
		if(t[x].L==t[x].R) return a[t[x].L];
		if(k>t[t[x].l].sm) return query(t[x].r,k-t[t[x].l].sm);
		return query(t[x].l,k);
	}
}T;
int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<=n;i++)
	{
		int x;cin>>x;
		a[x]=i,rt[i]=T.upd(1,n,x);
	}
	for(int i=1;i<=m;i++)
	{
		int u,v;cin>>u>>v;
		int fu=find(u),fv=find(v);
		if(fu==fv) continue;
		f[fu]=fv,rt[fv]=T.merge(rt[fu],rt[fv],1,n);
	}
	cin>>m;
	while(m--)
	{
		char op;cin>>op;
		if(op=='Q')
		{
			int x,k;cin>>x>>k;
			cout<<T.query(rt[find(x)],k)<<"\n";
		}
		else
		{
			int x,y;cin>>x>>y;
			int fx=find(x),fy=find(y);
			if(fx==fy) continue;
			f[fx]=fy,rt[fy]=T.merge(rt[fx],rt[fy],1,n);
		}
	}
	return 0;
}

P3521 [POI 2011] ROT-Tree Rotations

这道题也比较简单。还是考虑从叶子节点往跟去合并。
我们考虑开权值线段树，然后合并是简单的，就是相应的权值位置相加即可。
那么怎么统计答案呢？我们抓住一个性质：只能交换兄弟节点，而且这是二叉树！
所以我们的答案就是交换前和交换后的较大值即可。然后交换并不会影响这一个节点的子树的数值的多少（你不可能交换儿子把一个权值交换到别的子树对吧）。
那么这道题就做完了，复杂度是 \(\mathcal O (n\log n)\)。

#include<bits/stdc++.h>
#define pll pair<ll,ll>
#define fi first
#define se second
using namespace std;
const int N=2e5+5;
using ll=long long;
pll res;
ll ans;
int n;
struct SGT
{
	struct Node
	{
		int l,r,x;
	}t[N<<5];
	int cnt;
	SGT(){cnt=0;}
	int upd(int l,int r,int x)
	{
		int u=++cnt;t[u].x=1;
		if(l==r) return u;
		int mid=(l+r)>>1;
		if(x<=mid) t[u].l=upd(l,mid,x);
		else t[u].r=upd(mid+1,r,x);
		return u;
	}
	int merge(int u,int v,int l,int r)
	{
		if(!u||!v) return u|v;
		if(l==r)
		{
			t[u].x+=t[v].x;
			return u;
		}
		res.fi+=1ll*t[t[u].r].x*t[t[v].l].x;
		res.se+=1ll*t[t[v].r].x*t[t[u].l].x;
		int mid=(l+r)>>1;
		t[u].l=merge(t[u].l,t[v].l,l,mid);
		t[u].r=merge(t[u].r,t[v].r,mid+1,r);
		t[u].x+=t[v].x;
		return u;
	}
}T;
int solve()
{
	int u,v;cin>>v;
	if(!v)
	{
		int lc=solve(),rc=solve();
		res.fi=res.se=0;
		u=T.merge(lc,rc,1,n);
		ans+=min(res.fi,res.se);
	}
	else u=T.upd(1,n,v);
	return u;
}
signed main()
{
	cin>>n;solve();
	cout<<ans;
	return 0;
}

P5210 [ZJOI2017] 线段树

我有权利怀疑这道题的恶评成度。
首先建议去看看 splay。
然后这道题有个明显的结论：对于题中描述的一个树，无论他的树高多么诡异，对于这个线段树的控制区间 \([l,r]\) 来说，从 \(l-1\) 往 \(LCA(l,r)\) 跳的过程中的所有点（不包括 \(LCA(l,r)\)）的右孩子，以及 \(r+1\) 往 \(LCA(l,r)\) 跳的过程中的所有点（不包括 \(LCA(l,r)\)）的左孩子，这些区间的并集一定是 \([l,r]\)。
~~上面说的是什么 sb 东西。~~我们画个图来理解一下。

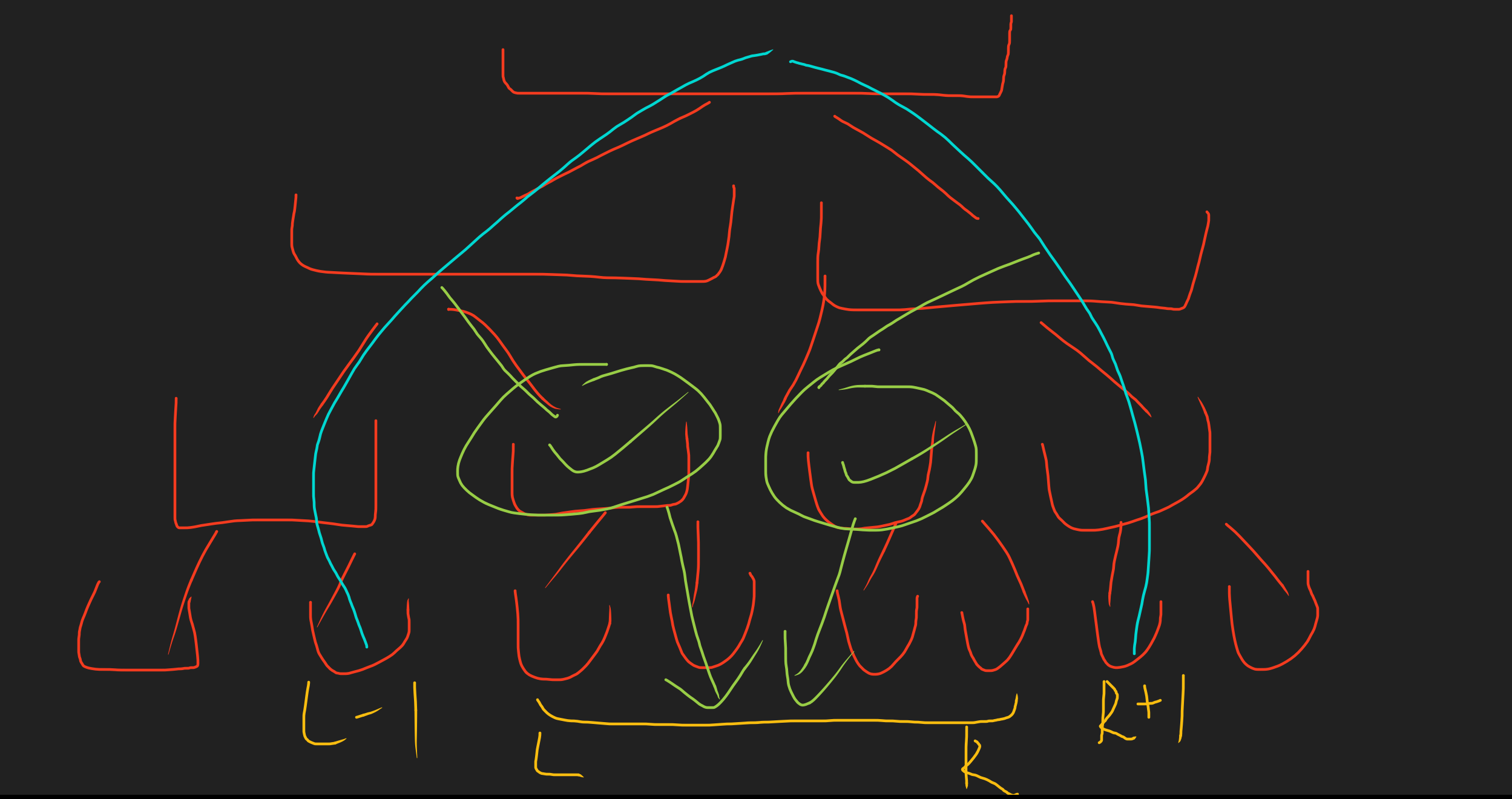
如上所示，我们发现这里 \(l-1\) 往 \(LCA(l,r)\) 跳的时候所有点的右节点是左边那个绿色节点；这里 \(r-1\) 往 \(LCA(l,r)\) 跳的时候所有点的右节点是右边那个绿色节点，这两个绿色节点拼起来正好是 \([l,r]\)！
然后这道题大概就做完了，你都知道是哪一些节点了还不好做吗？
我们设点权为 \(a_{1,\cdots,k}\)。那么我们要求的值就是：

\[\sum\limits_{i=1}^k dis(u,a_i) \]

怎么做呢？首先想到虚树，但是 \(\sum k\) 没有保证。
事实上，我们可以去用树上差分的方法去做上面的题目。
这里又有一个小技巧。我们可以考虑先去假设 \(u\) 是根节点，然后我们先求出所有关键节点到根节点的路径之和的值。然后分三类讨论。

如果 \(u\) 是 \(LCA(l,r)\) 的祖先，那么我们所需要做的就是减去 \(2*dep[u]*sum\)，
sum 表示路径和。
如果 \(u\) 在 \(LCA(l,r)\) 的左子树，我们发现右子树是没有任何影响的，然后至于左子树稍微维护一下就可以了（这真不知道咋讲了一会看代码吧，反正能看懂）。
在右子树同理，不说了。
预处理是 \(\mathcal O(n\log n)\) 的，算答案瓶颈是 LCA 的 \(\mathcal O(n\log n)\) 的，可以说非常的优秀，比题解里偷懒的大佬们的数据结构维护好些 \(n\) 倍。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e5+5;
int n,m,id,c[N][2],pos[N],rt,f[N][20],dfn[N],sz[N],TI,cnt[N][2],sum[N][2],dep[N];
int build(int l,int r)
{
	int u=++id;
	if(l==r) return pos[l]=u;
	int mid;cin>>mid;
	c[u][0]=build(l,mid);
	c[u][1]=build(mid+1,r);
	return u;
}
void dfs1(int x,int fa)
{
	dep[x]=dep[fa]+1,f[x][0]=fa,dfn[x]=++TI,sz[x]=1;
	for(int i=1;i<=18;i++)
		f[x][i]=f[f[x][i-1]][i-1];
	for(int i=0;i<2;i++)
		if(c[x][i])
			dfs1(c[x][i],x),sz[x]+=sz[c[x][i]];
}
void dfs2(int x)
{
	for(int i=0;i<2;i++)
	{
		if(!c[x][i]) continue;
		int v1=c[x][i],v2=c[x][i^1];
		for(int j=0;j<2;j++)
		{
			cnt[v1][j]=cnt[x][j];
			sum[v1][j]=sum[x][j];
		}
		if(v2)
		{
			cnt[v1][i^1]++;
			sum[v1][i^1]+=dep[v2];
		}
		dfs2(v1);
	}
}
int LCA(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=18;~i;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y) return x;
	for(int i=18;~i;i--)
	{
		if(f[x][i]==f[y][i]) continue;
		x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}
signed main()
{
	cin>>n;build(1,n);
	rt=++id,c[rt][0]=pos[0]=++id,c[rt][1]=1;
	rt=++id,c[rt][0]=rt-2,c[rt][1]=pos[n+1]=++id;
	dfs1(rt,0),dfs2(rt);
	cin>>m;
	while(m--)
	{
		int l,r,u;cin>>u>>l>>r;
		l=pos[l-1],r=pos[r+1];
		int L=LCA(l,r),ls=c[L][0],rs=c[L][1]; 
		int ans=sum[r][0]-sum[rs][0]+sum[l][1]-sum[ls][1]+dep[u]*(cnt[r][0]-cnt[rs][0]+cnt[l][1]-cnt[ls][1]);
		if(dfn[u]<=dfn[L]||dfn[u]>=dfn[L]+sz[L])
		{
			int LL=LCA(u,L);
			ans-=2*dep[LL]*(cnt[r][0]-cnt[rs][0]+cnt[l][1]-cnt[ls][1]);
		}
		else if(dfn[u]>=dfn[ls]&&dfn[u]<dfn[ls]+sz[ls])
		{
			int LL=LCA(u,l);
			ans-=2*dep[L]*(cnt[r][0]-cnt[rs][0]);
			ans-=2*dep[LL]*(cnt[l][1]-cnt[LL][1]);
			ans-=2*(sum[LL][1]-sum[ls][1]);
			ans+=2*(cnt[LL][1]-cnt[ls][1]);
			if(dfn[u]>=dfn[c[LL][1]]&&dfn[u]<dfn[c[LL][1]]+sz[c[LL][1]])
				ans-=2;
		}
		else
		{
			int LL=LCA(u,r);
			ans-=2*dep[L]*(cnt[l][1]-cnt[ls][1]);
			ans-=2*dep[LL]*(cnt[r][0]-cnt[LL][0]);
			ans-=2*(sum[LL][0]-sum[rs][0]);
			ans+=2*(cnt[LL][0]-cnt[rs][0]);
			if(dfn[u]>=dfn[c[LL][0]]&&dfn[u]<dfn[c[LL][0]]+sz[c[LL][0]])
				ans-=2;
		}
		cout<<ans<<"\n";
	}
	return 0;
}

posted @ 2025-05-24 16:35 I_AK_CTSC 阅读(16) 评论(0) 收藏举报

刷新页面返回顶部

IAKCTSC

线段树

逆序对