最短路笔记
最短路有 DIJ,死掉的算法,BELLMAN_FORD,Floyd。但是我们这里只讲 DIJ 和 Floyd。
DIJ好题
P4779 【模板】单源最短路径(标准版)
真的有什么好说的吗?
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5;
vector<pii> G[N];
int n,m,s,dis[N],vis[N];
priority_queue<pii> q;
void dij(int s)
{
memset(dis,0x3f,sizeof(dis));
q.push({0,s}),dis[s]=0;
while(!q.empty())
{
int x=q.top().se;q.pop();
if(vis[x]) continue;
vis[x]=1;
for(pii tmp:G[x])
{
int v=tmp.fi,w=tmp.se;
if(dis[v]>dis[x]+w)
{
dis[v]=dis[x]+w;
q.push({-dis[v],v});
}
}
}
}
int main()
{
cin>>n>>m>>s;
for(int i=1;i<=m;i++)
{
int u,v,w;cin>>u>>v>>w;
G[u].emplace_back(v,w);
}
dij(s);
for(int i=1;i<=n;i++)
{
if(dis[i]==0x3f3f3f3f) cout<<"-1 ";
else cout<<dis[i]<<" ";
}
return 0;
}
P2505 [HAOI2012] 道路
首先见到这种题,我们可以考虑正着做一遍 dij,然后我们就能得到有多少个点的最短路必定会经过 \(i\),那么至于剩下一半呢?我们反着做,然后就能找到一共有几个点会经过这个节点。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD=1e9+7,N=1505,M=5005;
typedef pair<int,int> pii;
int n,m,ans[M],cnt1[N],cnt2[N],dis[N],vis[N];
struct node
{
int v,w,id;
};
vector<node> G[N];
priority_queue<pii> q;
void dijkstra(int s)
{
memset(cnt1,0,sizeof(cnt1));
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
cnt1[s]=1;
q.push(make_pair(0,s));
vector<int> DG;
DG=vector<int>();
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u])
continue;
vis[u]=1;
DG.push_back(u);
for(node tmp:G[u])
{
int v=tmp.v,w=tmp.w;
if(dis[u]+w<=dis[v])
{
if(dis[u]+w==dis[v])
{
cnt1[v]=(cnt1[v]+cnt1[u])%MOD;
continue;
}
dis[v]=dis[u]+w;
cnt1[v]=cnt1[u];
q.push(make_pair(-dis[v],v));
}
}
}
reverse(DG.begin(),DG.end());
for(int u:DG)
{
cnt2[u]=1;
for(node tmp:G[u])
{
int v=tmp.v,w=tmp.w,id=tmp.id;
if(dis[u]+w==dis[v])
{
cnt2[u]=(cnt2[u]+cnt2[v])%MOD;
ans[id]=(ans[id]+1ll*cnt1[u]*cnt2[v]%MOD)%MOD;
}
}
}
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v,w;
cin>>u>>v>>w;
node tmp;
tmp.v=v,tmp.w=w,tmp.id=i;
G[u].push_back(tmp);
}
for(int i=1;i<=n;i++)
dijkstra(i);
for(int i=1;i<=m;i++)
cout<<ans[i]<<endl;
return 0;
}
P4644 [USACO05DEC] Cleaning Shifts S
简单来说,就是给你一些线段,问这些线段的并能使 \(S\) 到 \(E\) 联通。
看到这种区间覆盖的,很容易想到如下三种方法:
- 线段树/树状数组等区间数据结构
- 按左端点排序,然后看一个线段内有多少个左端点,然后建边。
我们采取第二种方法,我们先让线段首尾相连,边权为线段的权值,然后我们让这个线段的尾部与与这个线段相交的左端点连一条权值为 \(0\) 的边,然后就做完了。
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define se second
#define fi first
using namespace std;
const int N=300005,INF=0x3f3f3f3f3f3f3f3f;
int dis[N],n,M,E,vis[N];
vector<pii> G[N];
priority_queue<pii> q;
int dij(int s){
memset(dis,0x3f,sizeof(dis));
dis[s]=0,q.push({0,s});
while(!q.empty()){
int u=q.top().se;q.pop();
if(vis[u]) continue;
vis[u]=1;
for(pii tmp:G[u]){
int v=tmp.fi,w=tmp.se;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push({-dis[v],v});
}
}
}
return dis[E+1]==INF?-1:dis[E+1];
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>M>>E;
for(int i=M;i<E;i++)
G[i+1].emplace_back(i,0);//这样就不用二分的去找了
for(int i=1;i<=n;i++){
int u,v,w;cin>>u>>v>>w;
u=max(u,M),v=min(v,E);
G[u].emplace_back(v+1,w);
}
cout<<dij(M);
return 0;
}
P2371 [国家集训队] 墨墨的等式
经典的同余最短路。
我们假设去掉一个 \(a_n\),而我们把所有的 \(a_i\) 去与 \(a_n\) 取模数。
然后我们就能让 \(u\) 连向 \(u+a_i\) 一条边了,然后我们从 \(0\) 开始跑最短路。
最后我们根据前缀即可求出所有的情况。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20,M=5e5+5;
int n,l,r,mn=1e9,b[N],tot;
typedef pair<int,int> pii;
vector<pii>G[M];
priority_queue<pii> q;
int dis[M],vis[M];
int solve(int x)
{
int res=0;
for(int i=0;i<mn;i++)
if(dis[i]<=x)
res+=(x-dis[i])/mn+1;
return res;
}
signed main()
{
cin>>n>>l>>r;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
if(x)
{
b[++tot]=x;
mn=min(mn,x);
}
}
for(int i=0;i<mn;i++)
for(int j=1;j<=tot;j++)
if(b[j]!=mn)
G[i].push_back(make_pair((i+b[j])%mn,b[j]));
memset(dis,0x3f,sizeof(dis));
dis[0]=0;
q.push(make_pair(0,0));
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(vis[u])
continue;
for(pii tmp:G[u])
{
int v=tmp.first,w=tmp.second;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
q.push(make_pair(-dis[v],v));
}
}
}
cout<<solve(r)-solve(l-1)<<endl;
return 0;
}
P4473 [国家集训队] 飞飞侠
这道题是一道线段树优化建图的题。
我们建立 \(n\) 颗线段树,也就是对于每一行都建立线段树,然后这道题就相当于点连向区间,具体可以参考如下图。
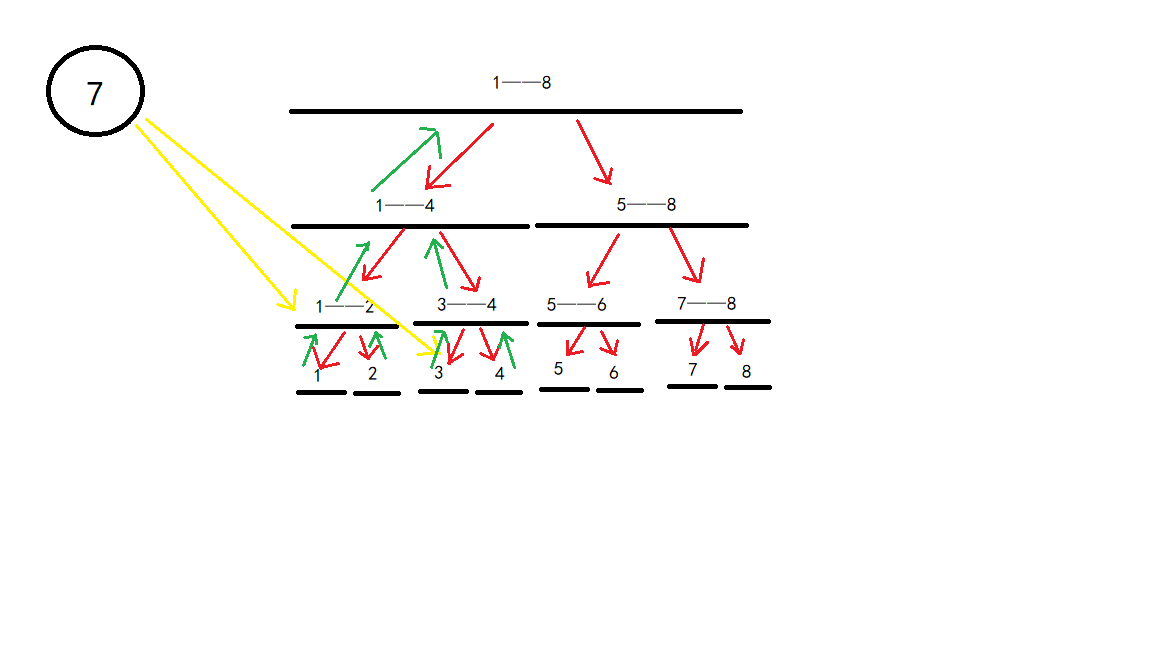
复杂度显然是对的。但是太难写了,以后再写吧(。
但是线段树优化建图给了我们一个很好的启示。我们知道,两个区间连边时候,会新建一个点使得建边的个数从平方变为线性。像这种建点优化的技巧,我们还会用。
Floyd以及好题
首先 Floyd 能用的前提是 \(n\) 能跑过 \(n^3\)。
Floyd 考点如下:
- \(k\) 的枚举顺序。
bitset优化传递闭包。- 考察 \(f[i][j]>f[i][k]+f[k][j]\) 的意义。
- 矩阵加速
P1119 灾后重建
这道题 \(k\) 按照 \(t\) 的顺序加边即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 205;
int t[N],q,f[N][N],n,m;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>t[i];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=(i==j?0:1e9);
for(int i=1;i<=m;i++)
{
int u,v,w;cin>>u>>v>>w;
u++,v++;
f[u][v]=f[v][u]=w;
}
cin>>q;
int lst=1;
while(q--)
{
int x,y,T;cin>>x>>y>>T;
x++,y++;
int pos=lst;
while(t[pos]<=T&&pos<=n)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][pos]+f[pos][j]);
pos++;
}
lst=pos;
if(t[x]>T||t[y]>T||f[x][y]==1e9) cout<<"-1\n";
else cout<<f[x][y]<<"\n";
}
return 0;
}
P1522 [USACO2.4] 牛的旅行 Cow Tours
这道题有一个适用于树的直径的性质。
这两个联通块的直径 \(A\) 和 \(B\) 合并后的直径有三种情况:
- 是 \(A\) 的直径。
- 是 \(B\) 的直径。
- \(A\) 连通块里从 \(i\) 点出发的最远路径 \(+\) \((i,j)\) 这一条边 \(+\) \(B\) 连通块里从 \(j\) 点出发的最远路径。
然后这道题就很平凡了。还有就是要判断两个点是否在一个联通块,我们选择并查集。
#include<bits/stdc++.h>
using namespace std;
const int N=155;
int fa[N],n,x[N],y[N];
double f[N][N],mx[N],MX[N];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
double dis(int x1,int y1,int x2,int y2){
return 1.0*sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=n;i++)
cin>>x[i]>>y[i];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(i==j) continue;
f[i][j]=1e9;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
char c;cin>>c;
if(i==j) continue;
if(c=='1'){
f[i][j]=dis(x[i],y[i],x[j],y[j]);
if(find(i)==find(j)) continue;
fa[find(i)]=find(j);
}
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
if(find(i)==find(j))
MX[i]=max(MX[i],f[i][j]);
mx[find(i)]=max(mx[find(i)],MX[i]);
}
double ans=1e9;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(find(i)!=find(j))
ans=min(ans,max({mx[find(i)],mx[find(j)],dis(x[i],y[i],x[j],y[j])+MX[i]+MX[j]}));
printf("%.6lf",ans);
return 0;
}
Cow Toll Paths G
这道题我们按照点权从小到大排序,然后按照点权的顺序枚举 \(k\)。
在进行 Floyd 的同时记录一个 \(ans[i][j]\) 来计算题目所要求的。
那么转移就是 \(ans[i][j]=min(ans[i][j],f[i][k]+f[k][j]+min(a[i],a[j],a[k]))\)。
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1005,M=1e4+5;
int f[N][N],ans[N][N],n,m,q;
pii a[N];
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
cin>>a[i].fi;
a[i].se=i;
}
sort(a+1,a+1+n);
memset(ans,0x3f,sizeof(ans));
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;i++)
f[i][i]=0;
for(int i=1;i<=m;i++){
int u,v,w;cin>>u>>v>>w;
f[u][v]=min(f[u][v],w);
f[v][u]=min(f[v][u],w);
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
int I=a[i].se,J=a[j].se,K=a[k].se;
f[I][J]=min(f[I][J],f[I][K]+f[K][J]);
ans[I][J]=min(ans[I][J],f[I][J]+max({a[i].fi,a[j].fi,a[k].fi}));
}
while(q--){
int l,r;cin>>l>>r;
cout<<ans[l][r]<<"\n";
}
return 0;
}
P6175 无向图的最小环问题
这道题就是在 Floyd 的基础上做了一点修改。
我们考虑怎么加入一个点然后变成一个环。
我们直接 \(ans=min(ans,f[i][j]+d[i][k]+d[k][j]\),然后正常做 Floyd 就行了。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
constexpr int N = 105;
int floyd[N][N], a[N][N];
signed main() {
cin >> n >> m;
memset(floyd, 0x2a, sizeof(floyd));
memset(a, 0x2a, sizeof(a));
for (int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
floyd[u][v] = floyd[v][u] = w;
a[u][v] = a[v][u] = w;
}
int ans = 0x2a2a2a2a2a2a2a2a;
for (int k = 1; k <= n; k++) {
for (int i = 1; i < k; i++)
for (int j = i + 1; j < k; j++)
ans = min(ans, a[i][k] + a[k][j] + floyd[i][j]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
floyd[i][j] = min(floyd[i][j], floyd[i][k] + floyd[k][j]);
floyd[j][i] = floyd[i][j];
}
}
if (ans >= 0x2a2a2a2a2a2a2a2a) cout << "No solution.\n";
else cout << ans << endl;
return 0;
}
P2419 [USACO08JAN] Cow Contest S
经典传递闭包。
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n,m,f[N][N],cnt;
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
f[u][v]=1;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=f[i][j]|f[i][k]&f[k][j];
for(int i=1;i<=n;i++){
bool flag=true;
for(int j=1;j<=n;j++){
if(i==j) continue;
if(f[i][j]||f[j][i]) continue;
flag=false;break;
}
if(flag) cnt++;
}
cout<<cnt;
return 0;
}
P2881 [USACO07MAR] Ranking the Cows G
传递闭包经典题。
但是这个需要 bitset 优化。
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m,cnt;
bitset<N> f[N];
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
f[u][v]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(f[j][i])
f[j]|=f[i];
for(int i=1;i<=n;i++)
cnt+=f[i].count();
cout<<(n-1)*n/2-cnt;
return 0;
}
P1841 [JSOI2007] 重要的城市
这道题就是考察 \(dis[i][j]>dis[i][k]+dis[k][j]\)。
我们知道,如果 \(dis[i][j]>dis[i][k]+dis[k][j]\),那么之前松弛过 \((i,j)\) 的那个点就没用了,因为最短路更新后不会有它。
最后一次更新 \(dis[i][j]\) 的那个店 \(k\) 就是 \((i,j)\) 的关键点。
#include <bits/stdc++.h>
using namespace std;
const int N = 205;
int F[N][N], IM[N][N];
int ans[N], cnt;
set<int> st;
int main() {
int n, m;
cin >> n >> m;
memset(F, 0x3f, sizeof(F));
for (int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
F[u][v] = F[v][u] = min(F[u][v], w);
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++) {
if (i == k) continue;
for (int j = 1; j <= n; j++) {
if (i == j || j == k) continue;
if (F[i][j] > F[i][k] + F[k][j]) {
F[i][j] = F[i][k] + F[k][j];
IM[i][j] = k;
} else if (F[i][j] == F[i][k] + F[k][j]) IM[i][j] = 0;
}
}
bool flag = false;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (i == j) continue;
if (IM[i][j]) flag = true, st.insert(IM[i][j]);
}
if (!flag) {
cout << "No important cities.\n";
return 0;
}
for (auto x : st) cout << x << " ";
cout << endl;
return 0;
}
P1690 贪婪的Copy
这道题就是 Floyd 求出任意两点的最短路,然后 \(\mathcal O(n!)\) 地去枚举宝藏区域即可。
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n,m,a[N],f[N][N];
int main(){
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>f[i][j];
cin>>m;
for(int i=1;i<=m;i++)
cin>>a[i];
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
sort(a+1,a+1+m);
int mn=1e9;
do{
int res=f[1][a[1]]+f[a[m]][n];
for(int i=1;i<m;i++)
res+=f[a[i]][a[i+1]];
mn=min(mn,res);
}while(next_permutation(a+1,a+1+m));
cout<<mn;
return 0;
}
P4306 [JSOI2010] 连通数
这道题跟最短路没啥关系,但是也是一道 bitset 的实际应用。
首先一眼可以缩点,然后对于缩点后的图跑拓扑排序。
现在就是一个关键的问题:如何统计他能到的所有的点呢?
我们考虑建反图,然后对每一个缩点后的节点建立一个 bitset,然后下放给他们拓扑序后面的节点即可。
复杂度 \(\mathcal O(\frac{n^3}{w})\),可以通过。
#include<bits/stdc++.h>
using namespace std;
const int N=2005;
int n,dfn[N],low[N],T,S[N],tp,in[N],SC,sz[N],bel[N],F[2005][2005],de[N];
vector<int> G1[N],G2[N];
queue<int> q;
bitset<N> f[N];
void tarjan(int x){
dfn[x]=low[x]=++T;
in[x]=1,S[++tp]=x;
for(int v:G1[x]){
if(!dfn[v]){
tarjan(v);
low[x]=min(low[x],low[v]);
}else if(in[v])
low[x]=min(low[x],dfn[v]);
}
if(low[x]==dfn[x]){
++SC;
while(true){
int u=S[tp];tp--;
f[SC][u]=1,bel[u]=SC;
sz[SC]++,in[u]=0;
if(u==x) break;
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
string s;cin>>s;
for(int j=1;j<=n;j++){
int x=s[j-1]-'0';
if(!x) continue;
G1[i].push_back(j);
}
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
for(int u=1;u<=n;u++)
for(int v:G1[u]){
int fu=bel[u],fv=bel[v];
if(F[fv][fu]||fu==fv) continue;
G2[fv].push_back(fu),de[fu]++;
F[fv][fu]=1;
}
int ans=0;
for(int i=1;i<=SC;i++)
if(!de[i]) q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
for(int v:G2[x]){
f[v]|=f[x];
if(!--de[v]) q.push(v);
}
}
for(int i=1;i<=SC;i++)
for(int j=1;j<=n;j++)
if(f[i][j])
ans+=sz[i];
cout<<ans;
return 0;
}
P6190 [NOI Online #1 入门组] 魔法
这道题是一个类 Floyd 题目。
首先我们设 \(f[i][j][k]\) 表示从 \(i\) 到 \(j\) 至多使用 \(k\) 次魔法的最短路。
鉴于我们的 \(k\) 是在 \(k-1,k-2,\cdots,1\) 都算过的,所以我们考虑从 \(k-1\) 转移即可。
复杂度为 \(\mathcal O(kn^3)\),如果实现的好,甚至能冲过 \(90\) 分!
好了,剩下 \(10\) 分呢?
别要了,再说我当年能拿 \(90\) 分都不知道能开心几辈子了……
我们发现,我们的优化范围只有 \(k\)。
观察可知,对于这个过程,我们可以从 \(k-1\) 转移到 \(k\),也就是一位一位的合并。所以很容易想到倍增。
呃呃呃呃呃…………发现倍增不好实现?不好实现,就用分治代替!
那么这道题对 \(k\) 分治。
同时我们考虑我们之前提到的但一直没有用的考点:二维矩阵
那么我们就可以轻松得出做法:矩阵快速幂。
我们先来观察 Floyd 的转移特点:
而标准矩阵是:
所以我们只需要把矩阵的 \(+\) 变为求 \(\min\) 即可!
时间复杂度是 \(\mathcal O(n^3\log k)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=105;
int n,m,u[2505],v[2505],w[2505],k,f[N][N];
struct Matrix
{
long long a[N][N];
friend Matrix operator *(const Matrix &A,const Matrix &B)
{
Matrix C;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
C.a[i][j]=0x3f3f3f3f3f3f3f3f;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int p=1;p<=n;p++)
C.a[i][j]=min(C.a[i][j],A.a[i][p]+B.a[p][j]);
return C;
}
}T;
Matrix ksm(Matrix A,int a)
{
Matrix res=A;a--;
for(;a;a>>=1,A=A*A)
if(a&1) res=res*A;
return res;
}
signed main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(i!=j) f[i][j]=0x3f3f3f3f3f3f3f3f;
T.a[i][j]=0x3f3f3f3f3f3f3f3f;
}
for(int i=1;i<=m;i++)
{
cin>>u[i]>>v[i]>>w[i];
f[u[i]][v[i]]=min(f[u[i]][v[i]],w[i]);
}
for(int p=1;p<=n;p++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][p]+f[p][j]);
if(!k) {cout<<f[1][n]<<"\n";return 0;}
for(int p=1;p<=m;p++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
T.a[i][j]=min({T.a[i][j],f[i][j],f[i][u[p]]+f[v[p]][j]-w[p]});
Matrix res=ksm(T,k);
cout<<res.a[1][n];
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号