关于在实验室的模拟训练

实验室第一次作业，不算很难，但模拟确实很考验细节和耐心。。

这是我会写的题目

J和K是最难的两道题

上传下我自己的题解吧！

​

模拟专题

​

 

A. Suffix Three

先来看题意：给定一个字符串，结尾是"po"的被称为Filipino语，"结尾desu"或者"masu"的被称为Japanese语，结尾是"mnida"的被称为Korean语 (不知真假)

好吧其实大家都看到了，这就是一道签到题，只需要判断字符串尾部就好了，或者说更直接一点看最后一个字母是什么就好了

如果是'a'结尾的是Korean语，'o'结尾的是Filipino语，'u'结尾的是Japanese语。

所以我们就直接上代码吧！

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 ​
 int main()
 {
     int t;
     cin >> t;
     while(t--)
     {
         string s;    //定义字符串s
         cin >> s;
         int m = s.size();
         if(s[m-1] == 'o') //结尾是o，所以是FILIPINO语
         cout << "FILIPINO";
         else if(s[m-1] == 'u')//结尾是u,所以是JAPANESE语
         cout << "JAPANESE";
         else cout << "KOREAN"; 
         printf("\n");
     }
     
     
   return 0;
 }

 

B. Dreamoon and Ranking Collection

先看题意吧：有个人在cf打比赛的排位为a1,a2....an序列，问在又进行x轮比赛后这个人的cf打过的比赛中排位最多从1连续到多少。换句话说，可以找到x个数插在a1到an序列后，找到最大v使得，1-v都在序列当中

很显然这也是道签到模拟题（看通过率还挺高的）

简单阐明下思路

 

本题数据量很小，所以我们直接暴力遍历即可，我们需要看从1一直往后有多少数需要补充，依次补充即可。在遍历之前，我们先定义一个f数记录是否需要补充。随后我们考虑有以下两种可能：

• v < 最大的数

• v >= 最大的数

   

为了能搞清楚v能不能大于最大的数，我们就先找到最大的数，然后从1开始遍历看看能不能大于等于n

（前面读取数据略过）

我们先定义变量cnt表明已经填充了多少数了

int cnt = 0;

然后就从1到最大的数开始遍历（这里我们假定maxn是最大的数）

 for(i=1;i<=maxn;i++)
     {
     if(!f[i])
         {
         if(cnt<x) //如果还能够补充
         cnt++;
         else break; //不能补充了就退出，此时i就表示 v+1
         }
     }

最后我们根据情况分类讨论输出就行了。

 if(i==maxn+1)//遍历结束了，v >= maxn
             printf("%d",maxn+x-cnt);
             else printf("%d",i-1); //v < n 直接输出 i-1
             printf("\n");

 

下面附上本蒟蒻代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 bool f[105];  //标记是否需要填充
 int main()
 {
     int t;
     cin >> t;
     while(t--)
     {
         memset(f,false,sizeof(f)); //初始化
         int n,x,cnt=0,i,maxn;
         cin >> n >> x;
         cin >> maxn;
         f[maxn]=true;
         for(i=2;i<=n;i++)
         {
             int m;
             scanf("%d",&m);
             if(m > maxn)   //找maxn，也可以直接用max函数
             maxn = m;
             f[m] = true;
         }
         for(i = 1; i <= maxn; i++)
         {
             if(!f[i])
             {
                 if(cnt < x)//如果还能够补充
                 cnt++;
                 else break;//不能补充了就退出，i = v + 1
             }
         }
             if(i == maxn+1)//遍历结束了，v >= maxn
             printf("%d",maxn + x - cnt);
             else printf("%d",i-1);//v < n 直接输出 i-1
             printf("\n");
     }
 ​
     
   return 0;
 }

 

C. Symmetric Matrix

symmetric是“对称的”意思，相信聪明的你肯定知道的

先看题意： 有无数个给定的2×2正方形，问你是否能根据这些矩形构造出一个给定m × m的对称正方形。一个对称正方形的定义是这样的：s[ i ] [ j ] = s[ j ] [ i ]

思路：

其实这道题看起来很难实际上很简单，因为它没有要求我们用上每一个，所以只要有一个满足，我们就可以将这个正方形拼上去拼成我们想要的这个正方形（当然也有可能拼不上，我们待会儿再讲）

那么问题来了，到底什么样的正方形才能算是满足的呢？

这个解释起来有点困难，我们可以画图看下

首先我们考虑4 × 4的正方形（这图一定画得很好）

 

当 i = j 的时候肯定是相等的

 

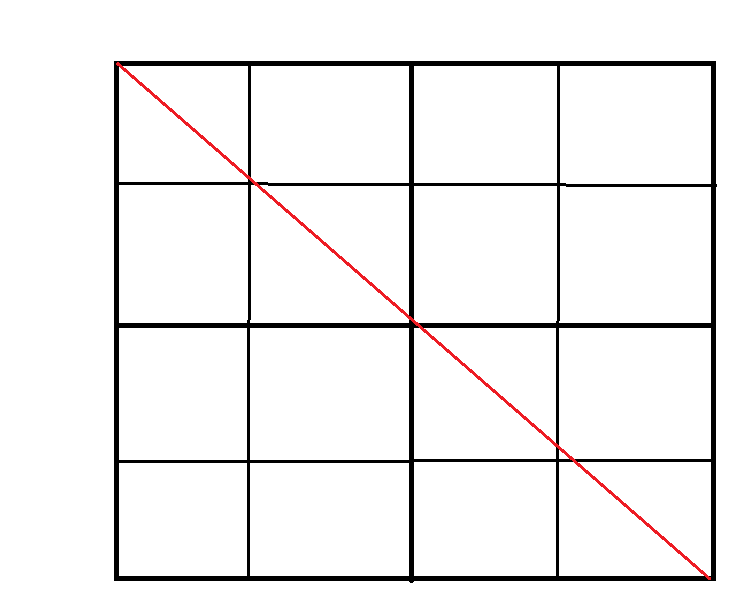
否则，我们只需要满足拿出来构造的正方形的另一条对角线的数相等就行了，其余情况都是可以根据构造的三角形自身对称来做到

 

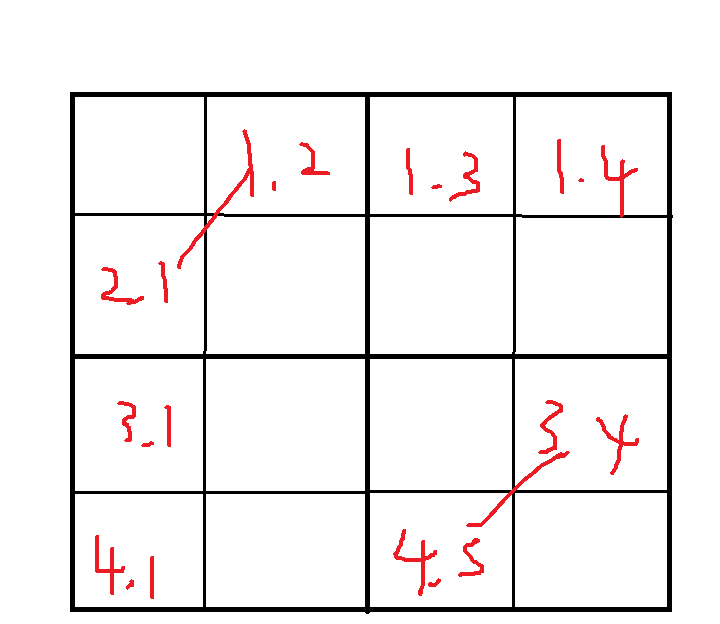
这是 4×4的正方形，那么我们再考虑n × n呢？

我们会发现可以把n × n分解成四块

 

同样可以一直细分下去（时间关系图就不补充完了），最后我们只要构造的小正方形满足，整个大正方形就可以满足了。

好此题结束

还有一种可能，2×2的正方形不能构造出m×m的正方形，也就是说，m为奇数是，是不可能构造出来的。所以我们还需要判断下m的奇偶性即可。

话不多说，上代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 ​
 ​
 ​
 int main()
 {
     
     int t;
     cin>>t;
     while(t--)
     {
         int n,m,cnt=0,a,b,c,d;
         cin>>n>>m;
          for(int i=0; i<n; i++)
          {
             scanf("%d %d",&a,&b);
             scanf("%d %d",&c,&d);
             if(b == c)
             cnt++;
          }
          if((!(m & 1)) && cnt)//判断是否有满足条件的正方形
                                        //与判断奇偶性
          cout << "YES";
          else cout << "NO";
          printf("\n");
     }   
   return 0;
 }

D. Happy Birthday, Polycarp!

先看题意：漂亮数是指数位中只有一个数的数。给定一个n，求1到n（包括n）有多少个漂亮数。

我乍一眼，以为是数位dp

好的吧，其实思路是这样的：

首先我们考虑若n是一位数，由于小于10的数都是漂亮数，所以就有1，2，····,n共n个漂亮数

其次，我们再看万一n有两位数以上

我们拿494564举例，这个数有六位数，所以所有五位数以及以下的漂亮数都可以，我们从相同的数字入手，由于第一位不能是0，所以相同的数字可以是1到9，设这个数有cnt位，则在100000以前的漂亮数有（cnt - 1）* 9个，我们现在只需要考虑从100000到494564有多少个漂亮数。我们要从头考虑，当首位是1,2,3时都是可以的（因为111111 222222 333333 首位都小于4，所以后面无论多大都没用）

所以，现在我们的难点是考虑相同数字为最高位且位数与这个数一样多的数字行不行。换句话说：设最高位为m，位数为q，我们需要考虑mm····mm(总共有q个m)的数是否大于n就行了。

理清了思路，我们就可以看看代码怎么写的了：

 #include<bits/stdc++.h>
 using namespace std;
 int cnt;   //判断这个数有多少位
 int fx(int n) //这个函数既判断了有多少位数，又找到了最高位
 {
     cnt = 1;
     while(n/10!=0)
     {
         cnt++;
         n = n / 10;
     }
     return n;  //此时n就是这个数的最高位
 }
 int times(int m,int q)  //乘以10的函数
 {
     int i;
     for(i = 1; i < q; i++)
     {
         m = m*10;
     }
     return m;
 }
 int main()
 {
     
     int t;
     cin >> t;
     while(t--)
     {
         int n, num, m = 0, s = 0;
         scanf("%d",&n);
         if(n < 10)
         {
         printf("%d\n",n);
         continue;
         }  //如果小于10，直接输出n
         
         num=fx(n); //num表示这个数的最高位是多少
         for(int i=cnt;i>1;i--)
         {
             m = m + times(num,i); 
         }
         m+=num;  //构造上述的mm··mm看看是否满足
         if(m > n) //m不在里面
         s--;
         s += num + (cnt - 1) * 9;// 算出漂亮数个数
         printf("%d\n",s);
         
     }   
   return 0;
 }

E. A New Technique

先看大概题意：有个n×m的矩形，以乱序给出每行和每列，要求你还原这个矩形。

好的，其实这也是道简单题

我们可以这样考虑：

在给出的每行中，我们知道了每个数字的列坐标

比如给出了： 6 5 4

那我们就知道了6肯定在第一列，5在第二列，4在第三列

同理，在给出的每列中，我们就知道了每个数字的行坐标

比如给出了：1 6

那我们就知道1在第一行，6在第二行。

由于数字不重复，因此每个数字的行坐标和列坐标就被唯一确定了。而由于这个唯一性，我们考虑用map存储行列坐标，让数字直接映射到map的值

因此，这里直接附上代码：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<map>
 #include<algorithm>
 using namespace std;
 map<int,int>a; //存储行坐标
 map<int,int>b; //存储列坐标
 int c[505][505]; //对应的数字存储
 ​
 int main()
 {
     int t;
     cin >> t;
     while(t--)
     {
         
         int n,m;
         cin >> n >> m;
         for(int i = 1; i <= n; i++)
         {
             for(int j = 1; j <= m; j++)
             {
                 int q;
                 cin >> q;
                 b[q] = j; //保存列坐标
             }
         }
         for(int i = 1; i <= m; i++)
                 {
                     for(int j = 1;j <= n; j++)
                     {
                         int q;
                         cin >> q;
                         a[q] = j;//保存行坐标
                     }
                 }
                 for(int i=1;i<=n*m;i++)
                 c[a[i]][b[i]] = i;//保存到原来的数组里
                  
                 for(int i=1;i<=n;i++)
                 {
                     for(int j=1;j<=m;j++)
                     printf("%d ",c[i][j]);//输出数组
                     printf("\n");
                 }
                 
     }
     return 0;
 }

F. Reachable Numbers

题意：给定一个n，问不断加上1并且每次操作后去掉尾部的所有0（如果有的话），试问这样操作后有多少个数（注意加上n本身）

思路：

我们先考虑这样操作后什么时候会结束，显然这样不断操作总会出现尾部有0，而尾部有0就去掉，这样会导致这个数的位数越来越少直至最后成为个位数，而个位数不断加1会变成10，10去掉0以后又变成1，然后继续在个位数里面循环。

因此我们发现了，所有个位数总是包括在里面

所以我们模拟上述过程即可，现附上代码：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 ​
 int main()
 {
    int n,cnt = 9; //先加上9个个位数
    cin >> n;
    while(n>=10) //循环条件
     n++; //这样做是保证了这个数不会被先筛掉
     while(n % 10 == 0) 去掉尾部的所有0
        n = n / 10;
        cnt++;
    }
    cout << cnt;
     return 0;
 }

我们注意到上述的代码中并没有考虑n本身，但结果是对的，因为在最后一次中我们多进行了了一次cnt++，就比如当n为2时，显然应该要退出循环了，但是我们还是进行了一次cnt++，这样多加的一次刚好与n本身少的那一次抵消。

G. Collecting Packages

题意：机器人取货，只能往右或往上走，给了n个包裹的坐标，问是否能做到顺路取完所有。

思路：我们首先考虑能不能顺路取完。因为机器人只能往右或者往上走，所以对于每个包裹，在它右边的包裹都必须在它的上方。

换句话说，如果有一个包裹在一个包裹的右下方，那显然是不能顺路取完的

为了解决这个问题，我们就需要对包裹坐标排序,所以我们将包裹的坐标放在结构体中方便排序（其实pair似乎也可以，本蒟蒻不是很熟练）

接下来跟着题目思路走就行了，这里我们采用string保存路径

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<string>
using namespace std;
int a[1001];
int b[1001];
struct pa
{
	int x;
	int y;
}package[1001];  //封装成结构体
bool cmp(pa m,pa q)
{
	if(m.x == q.x)
	return m.y < q.y;
	return m.x < q.x;
}  //排序函数，注意在横坐标相等时比较纵坐标
void finding(int n)
{
	string s;
	
	for(int i = 0 ; i < n ; i++)
        scanf("%d%d",&package[i].x,&package[i].y); //读取数据
	    sort(package,package+n,cmp);
	    for(int i = 0 ;i < package[0].x ; i++) //在到达第一个包裹前的路径
		s.push_back('R');
		for(int i = 0 ;i < package[0].y ; i++)
		s.push_back('U');
	    for(int i = 1 ; i < n ; i++)
	     {
			if(package[i].y<package[i-1].y) //判断是否可以一次性拿完。
			{                       //由于我们排过序了，直接比较纵坐标就行了
				cout << "NO" << '\n';
				return;
			}
			
			for(int j = package[i-1].x ; j < package[i].x ; j++)
					s.push_back('R');
			for(int j = package[i-1].y ; j < package[i].y ; j++)
					s.push_back('U');
				//模拟路径
		 }
		 cout << "YES" << '\n';
		 cout << s << '\n';
}
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
       int n;
       cin >> n;
    finding(n);
    }
    
    
    return 0;
}

H. Yet Another Crosses Problem

先看题意吧：对于一个n×m矩阵，每个点是黑的或者白的，问要将多少个白的变黑的使得至少有一行和一列是黑的。

这道题一定要开string数组，不然会超出范围！！！

思路：记录每行每列有多少个白的（需要填充多少个），然后遍历每个点，查看以每个点为中心需要的最少的操作使得这个点所在的行列都为黑色。

按照思路模拟即可：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;
const int maxn = 5e4+5;
string str[maxn]; //关键：开string数组

int h[maxn],l[maxn]; //记录每行每列的白色的个数
const int inf = 4e+5 +5;
int main()
{
    int q,n,m;
    scanf("%d",&q);
    while(q--)
    {
        memset(h,0,sizeof(h)); 
        memset(l,0,sizeof(l)); //初始化数组
        scanf("%d %d",&n,&m);
        for(int i = 0; i < n; i++)
        cin >> str[i];
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                if(str[i][j] == '.')
				{
                  h[i]++;
				  l[j]++;
				}
            }
        }
       
        int ans=0,minn=inf;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                if(str[i][j] == '.')
                ans = -1; //如果这个点是白色的话，就多算了一次，所以ans = -1
                else
                ans = 0;
                if(h[i] + l[j] + ans < minn)
                minn = h[i] + l[j] + ans;
            }
        }
        printf("%d\n",minn);
    }
    return 0;
}

I. RGB Substring (easy version)

题意：给定一个只含有 ‘R’ 'G' 'B'的字符串，问操作多少次可以使其含有长度为k的顺序类似为RGBRGBRGB的子串。换句话说，该子串中R后面一定是G，G后面一定是B，B后面一定是R。

思路：由于数据量小（数据量大的我不会），我们可以暴力遍历，由于有 RGB GBR BRG这三种情况，所以我们在遍历时必须判断这三种情况。

按思路模拟即可：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
char s[20005];
char a[3] = {'R','G','B'};
int main() {
    int q;
    cin >> q;
    while(q--)
    {
        int n,k,ma = 1e+8, cnt;


        cin >> n >> k;
        cin >> s;
        for(int i = 0; i < n-k+1; i++)
        {
            int s1 = 0, s2 = 0, s3 = 0;
            for(int j = 0; j < k; j++)
            {

                cnt = 1e+9;
                if(s[i+j] != a[j%3])
                    s1++;
                if(s[i+j] != a[(j+1)%3])
                    s2++;
                if(s[i+j] != a[(j+2)%3])
                    s3++;
            }
            cnt = min(min(s1,s2),s3);
            ma = min(cnt,ma);
            if (ma == 0)
                break;
        }

        cout << ma << '\n';
    }
    return 0;
}

J. System Testing

题意：这题难在读题，意思很简单，有n个问题，而可以同时进行k个判断过程，问有多少个测试q，使得q = 四舍五入（目前任务完成率）

思路不好解释，我们直接看代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int N = 2e+5 +5;
int a[N],b[N],c[N];  //a数组储存测试点，b数组表示当前在搞的测试点  c数组表示测试点到几个了
bool vis[N];      //表示是否被测试过了
int main() {
    int n,k,cur,task = 0,ans = 0; //task表示已经完成了多少个任务了
    cin >> n >> k;
    cur = k + 1;       //cur表示目前进行到了第几个了
    memset(vis,false,sizeof (vis)); // 初始化
    for(int i = 1; i <= n; ++i)

        cin >> a[i];
    for(int i=1;i<=k;i++)
        b[i] = a[i];
    while(task < n)
    {
        int q = task *100.0/n +0.5;  //由于我们模拟的是每秒，所以将q现在最前面
                                    //每次循环都是一秒，+0.5为四舍五入
        for(int i = 1; i <= k; ++i) {
            if (!b[i]) continue;  //当前没有任务
            ++c[i];      //完成了一次提交的测试
            if(c[i] == q && !vis[i]) //测试完的数目刚好等于完成率
            {
                ++ans;
                vis[i] = true; //防止重复计数。
            }

            if(c[i] == b[i])
            {
                ++task; //任务数 + 1
                vis[i] = false;
                c[i] = 0;
                b[i] = a[cur++]; //继续新的任务测试

            }
        }

    }
    cout << ans;
    return 0;
}

K. Busy Robot

这道题和J一样烦人

题意：一个机器人在横轴上来回横走，每次接到一个命令走到x点，在完成命令前其他命令不管用，问有多少个命令是成功的。成功的命令指机器人既在某个命令指定的x点，又在这个命令的到下个命令的时间段内。

同样，我们用代码看思路：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;   //切记开long long
const int N = 1e+5 +5;
ll a[N],b[N];   //a数组存储时间，b数组存储x点
ll find(int j, int i, int s)
{
    return fabs(b[j] - s) + a[i];   //计算该到达j位置的时间
}
int main() {
    int m;
    cin >> m;
    while(m--) {
        ll n,i,t,s = 0, cnt = 0, q;  //t表示当前时间，s表示当前所在位置
        bool flag;         //flag表示是往右边走还是往左边走
        cin >> n;
        scanf("%lld %lld",&a[0],&b[0]);
       
        t = a[0];   //从第一个时间开始
        for(i = 1; i < n; ++i)
            scanf("%lld %lld",&a[i],&b[i]);
        i = 0;
        a[n] = 1e+12;  //表示最后一个时间为正无穷
        while(i < n)
        {
            if(b[i] > s)  
                flag = true ;   //命令在右边  
            else flag = false;  //命令在左边
            int f = fabs(b[i] - s);  //当前所在位置距离要到的点的位置
            if(t + f <= a[i+1])  //下达下个命令之前已经到了目标点
            {
                ++cnt;
                s = b[i];  //s更新
                ++i;
                t = a[i];   //t更新
            }
            else     //中间有命令忽略了
            {
                q = lower_bound(a,a+n,t+f) - a;  //找到范围
                for(int j = i + 1; j < q && j < n; ++j)
                {
                    if(flag && b[j] > s && b[j] <= b[i]) //
                    {
                        ll y = find(j,i,s);  //计算到达目标的时间
                        if(y >= a[j] && y <= a[j+1])
                            ++cnt;
                    }
                    else if(!flag && b[j] < s && b[j] >= b[i])
                    {
                        ll y = find(j,i,s);  //与上面同理
                        if(y >= a[j] && y <= a[j+1])
                            ++cnt;
                    }
                }
                s = b[i]; //更新当前点
                i = q;
                t = a[i]; //更新当前时间
            }

        }
        cout << cnt << '\n';
    }
    return 0;
}

L. 神奇的幻方

终于到了中文题了

这题过于简单，所以就不讲了

上代码

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
int a[45][45];
int b[1600];  //横坐标
int c[1600];  //纵坐标
int main() {
    memset(a,0,sizeof(a));
    int n,cnt = 2;
    cin >> n;
    int m = n*n;
    b[1] = 1;
    c[1] = (n>>1)+1;
    a[b[1]][c[1]] = 1;
    while(cnt <= m)
    {
        int x= b[cnt - 1],y = c[cnt - 1];
        if(x == 1 && y != n)
        {
            b[cnt] = n;
            c[cnt] = y +1;
        }
        else if(x != 1 && y == n)
        {
            b[cnt] = x - 1;
            c[cnt] = 1;
        }
        else if(x == 1 && y == n)
        {
            b[cnt] = 2;
            c[cnt] = y;
        }
        else
        {
            if(!a[x-1][y+1])
            {
                b[cnt] = x-1;
                c[cnt] = y+1;
            }
            else
            {
                b[cnt] = x+1;
                c[cnt] = y;
            }
        }
        a[b[cnt]][c[cnt]] = cnt;
        ++cnt;
    }
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            printf("%d ",a[i][j]);
        }
        printf("\n");
    }

    return 0;
}