打卡

1.问题：自守数是指一个数的平方的尾数等于该数自身的自然数。例如：
52 = 25 , 252 = 625 , 762 = 5776 , 93762 = 87909376
求100000以内的自守数

2.思路：

本问题所关心的是积的最后三位。分析产生积的后三位的过程可以看出，在每一次的部分积中，并不是它的每一位都会对积的后三位产生影响。总结规律可以得到：在三位数乘法中，对积的后三位产生影响的部分积分别为：

✪ 第一个部分积中：被乘数最后三位×乘数的倒数第一位。

✪ 第二个部分积中：被乘数最后二位×乘数的倒数第二位。

✪ 第三个部分积中：被乘数最后一位×乘数的倒数第三位。

将以上的部分积的后三位求和后，截取后三位就是三位数乘积的后三位，这样的规律可以推广到同样问题的不同位数乘积中。

3.程序流程图：

 

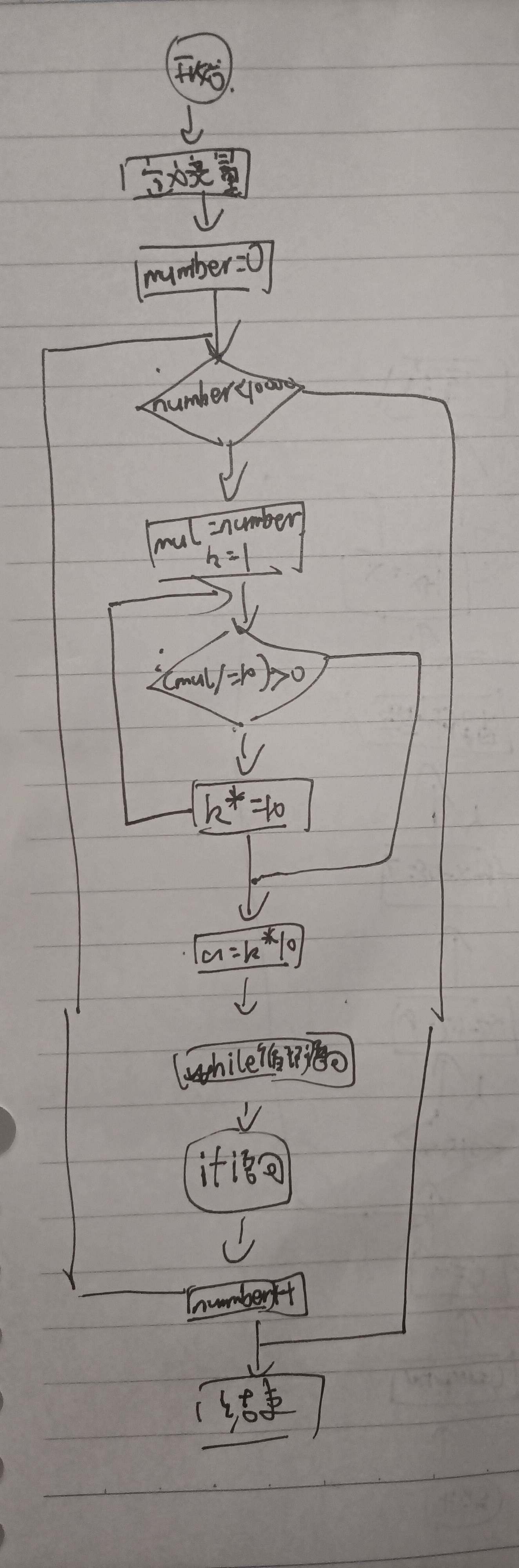
4.代码实现：

#include <iostream>
using namespace std;

int fact(string str,string str1)
{
for(long long i=str.size()-1,j=str1.size()-1;i>=0;i--,j--){
if(str[i]!=str1[j])
return 0;
}
return 1;
}
int main()
{
int count=0;
for(long i=0;i<=100000;i++){
long long k=i*i;
string str=to_string(i);
string str1=to_string(k);
if(fact(str,str1)){
count++;
cout<<"自守数为"<<i<<endl;
}
}
cout<<"从1到100000自守数总数为"<<count<<endl;
return 0;
}