打卡

1.问题：爱因斯坦出了一道这样的数学题：有一条长阶梯，若每步跨2阶，则最后剩一阶，若每步跨3 阶，则最后剩2阶，若每步跨5阶，则最后剩4阶，若每步跨6阶则最后剩5阶。只有每次跨7阶，最后才正好一阶不剩。请问在1到N内，有多少个数能满足？

2.思路：利用一个函数将每个条件表示并进行判断，然后在主函数中通过两个while循环来遍历1~N所有的数，然后用一个count变量来计数即可。

3.程序设计图：

 

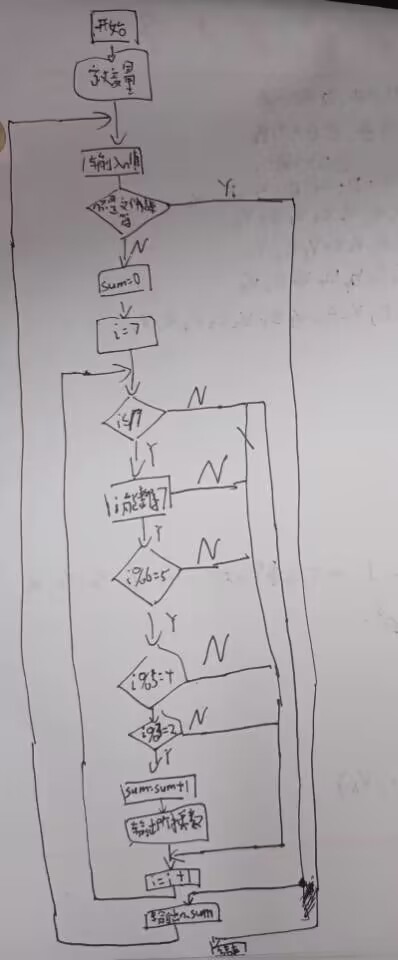
4.代码实现：

#include <iostream>
using namespace std;

int fact(int x)
{
if(x%2==1){
if(x%3==2){
if(x%5==4){
if(x%6==5){
if(x%7==0)
return 0;
}
}
}
}
return 1;
}
int main()
{
int N;
cin>>N;
int i=1;
int count=0;
while(i<=N){
int k=1;
while(k>0){
if(i>N){
count--;
break;
}
k=fact(i);
i++;
}
count++;
if(i<=N){
cout<<i-1<<" ";
}
}
cout<<count<<"个阶梯数";
}