【论文阅读】Zero-Reference Low-Light Enhancement via Physical Quadruple Priors(CVPR2024)
概要
- 任务领域:低光增强;零样本/无参考;RGB域
- 针对问题:零参考是成功的,但是缺少光照概念,依赖手工设置。
- 解决方法:基于Kubelka-Munk理论,设计物理四先验作为低光和正常光的不变要素,再利用生成模型将先验转为图像。
- 主要创新:物理四先验的设计;先验到图像的映射。
- 最终表现:优于大多数无监督方法,显著缩小与有监督方法的差距,在不同数据集中不错的泛化能力。
相关链接
论文链接:https://arxiv.org/abs/2403.12933
代码链接:https://github.com/daooshee/QuadPrior
正文
(1)Kubelka-Munk理论
\[E(\lambda,x)=e(\lambda,x)((1-i(x))^2R_\infty(\lambda,x)+i(x))
\]
其中,e表示光源的光谱,i表示镜面反射,$ R_\infty $表示材料反射率。
特例:当物品无光泽(matte)时,i≈0,那么上式退化为
\[E(\lambda,x)=e(\lambda,x)R_\infty(\lambda,x) \]也就是我们常见的Retinex理论。
(2)思路和推导
Retinex分解具有挑战性,所以改成从输入图像中提取光照不变特征,之后再生成光照相关信息来重建图像。
个人拙见
Retinex理论是一种理想的假设,分解本身是高度不适定的(highly ill-posed),所以挺依赖人为设计的反射和照度。
分解中丢掉了一些信息及噪声,分解之后还存在噪声变化,噪声残余等等杂七杂八的问题。

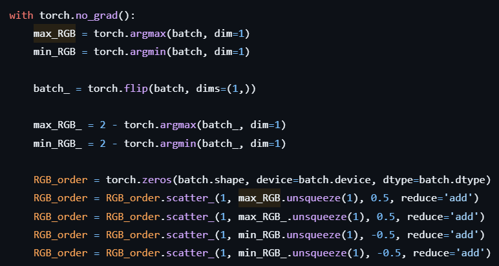
如图所示,在训练时,可以在正常光下进行,毕竟需要的是光照不相关信息。
为了得到光照不变量,得将Kubelka-Munk中的i和e消除掉!
HCWO
一些说明
\[E^\lambda=\frac{\partial E(\lambda, x)}{\partial \lambda}, R_\infty^\lambda=\frac{\partial R_\infty(\lambda, x)}{\partial \lambda},
E^{\lambda\lambda}=\frac{\partial^2 E(\lambda, x)}{\partial \lambda^2}, R_\infty^{\lambda\lambda}=\frac{\partial^2 R_\infty(\lambda, x)}{\partial \lambda^2}
\]

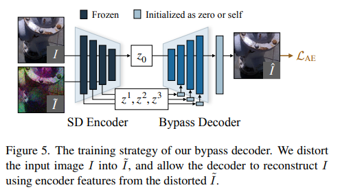
整体框架

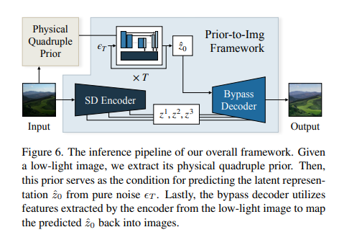
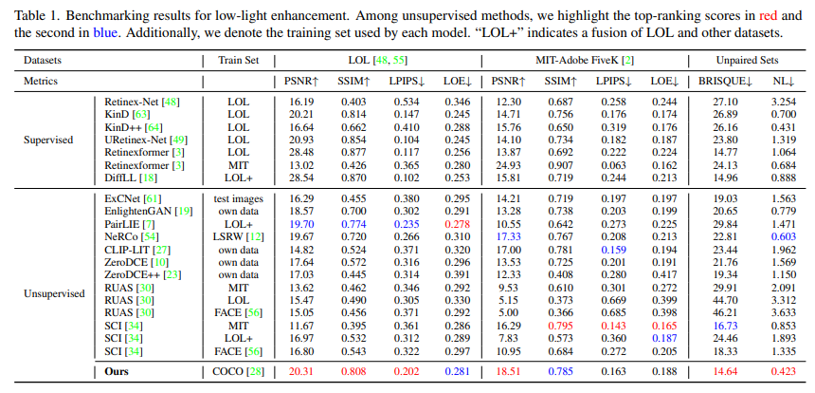
实验
定量和定性比较

消融

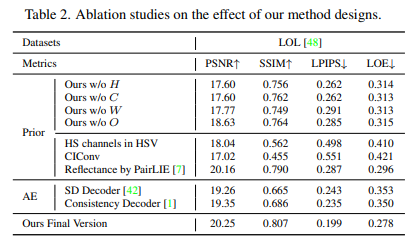



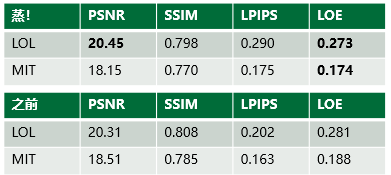
!过几天进行补充 😛
感想
(1)论文思路整体是非常清晰的,读起来很流畅,消融实验也很充分,值得参考。
(2)才发现作者也是Retinex-Net作者之一,太强啦!用物理解释性强的公式来解决这些问题,挺不错的。
(3)作为此处的首篇博文,可能整理得并不是特别好,正在研究中...





 浙公网安备 33010602011771号
浙公网安备 33010602011771号