树链剖分笔记
什么是树链剖分?
具体来说,树链剖分就是将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
树链剖分(树剖/链剖)有多种形式,通常指 重链剖分,可以将树上的任意一条路径划分成不超过 \(\log{n}\) 条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 LCA 为链的一个端点)。
重链剖分可以将树上的任意一条路径划分成不超过 \(\log{N}\) 条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 LCA 为链的一个端点)。
重链剖分还能保证划分出的每条链上的节点 DFN 序连续,因此可以方便地用一些维护序列的数据结构(如线段树)来维护树上路径的信息。(改编自 OI-wiki)
题目大意:已知一棵包含 N 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
1 x y z,表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。2 x y,表示求树从 x 到 y 结点最短路径上所有节点的值之和。3 x z,表示将以 x 为根节点的子树内所有节点值都加上 z。4 x,表示求以 x 为根节点的子树内所有节点值之和。
剖分树链
对于一个父节点 \(u\),将它的子节点分成两类:
- 重子节点:有且仅有一个,为 \(u\) 孩子中子树最大的点(除叶子节点外,树上的任意点都有重子节点,为了保证划分出的每条链上的节点 DFN 序连续,我们需先遍历重子节点)。
- 轻子节点:\(u\) 的子节点中,除了重子节点之外的点。
同时,重子节点与 \(u\) 的边被称为重边,反之为轻边。
对于重子节点,会将其加入 \(u\) 所在的树链中,其他的轻子节点则会作为一条新链的顶点(注:根节点属于轻子节点)。如下图:
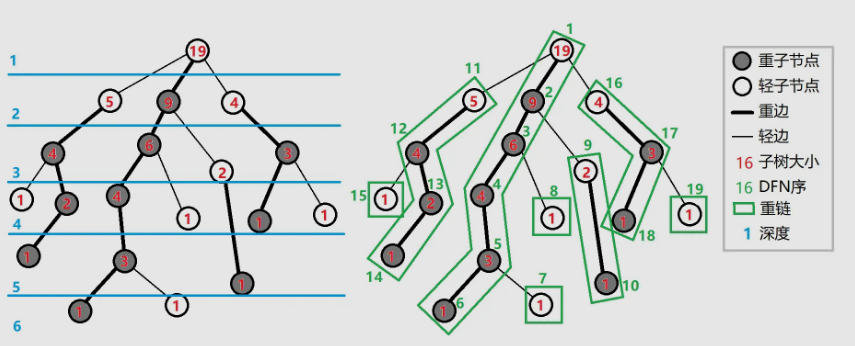
我们需用两次 DFS 来得出任意一节点 \(x\) 的以下值:
第一次 DFS:\(w_x\)(\(x\) 的重子节点),\(sze_x\)(\(x\) 的子树大小),\(dep_x\)(\(x\) 的深度),\(fa_x\)(\(x\) 的父亲);
第二次 DFS:\(dfn_x\)(\(x\) 的 dfn 序),\(top_x\)(\(x\) 所在的链的顶端)。
具体代码:
int fa[N], dep[N], sze[N], w[N];
void dfs(int x, int f)
{
int mx = 0; sze[x] = 1;
fa[x] = f; w[x] = -1;
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to == f) continue;
dep[to] = dep[x] + 1;
dfs(to, x), sze[x] += sze[to];
// 更新重子节点
if(mx < sze[to]) mx = sze[to], w[x] = to;
}
}
int dfn[N], cnt, top[N];
void dfs2(int x, int tp)
{
top[x] = tp;
dfn[x] = ++ cnt;
b[dfn[x]] = a[x];
if(w[x] == -1) return ;
dfs2(w[x], tp); // 先遍历重子节点,保证划分出的每条链上的节点 DFN 序连续
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to != fa[x] && to != w[x])
dfs2(to, to);
}
}
线段树
使用线段树维护区间 \([l, r]\) 的权值和(\(l\) 与 \(r\) 为 dfn 序,下面代码中 add_seg 为修改,query_seg 为查询)。
处理树链
- 将 \(x\) 到 \(y\) 结点的最短路径所经过点的权值加上 \(z\):
- 选取 \(x\) 与 \(y\) 之中链顶更浅的点 \(v\)(即 \(dep_{top_v} = \min{(dep_{top_x}, dep_{top_y})}\),此处钦定 \(v\) 为 \(y\)),在线段树中将区间 \([dfn_{top_v}, dfn_v]\) 加上 \(z\),把 \(v\) 跳到 \(fa_{top_v}\);
- 重复 1. 步骤,直到 \(top_x = top_y\);
- 将区间 \([dfn_x,dfn_y]\)(钦定 \(dep_x \le dep_y\))加上 \(z\)。
void add_path(int x, int y, int k)
{
k %= p;
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]])
swap(x, y);
add_seg(1, dfn[top[y]], dfn[y], k);
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
add_seg(1, dfn[x], dfn[y], k);
}
- 链的查询与修改相似:
int query_path(int x, int y)
{
int res = 0;
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]])
swap(x, y);
res = (res + query_seg(1, dfn[top[y]], dfn[y])) % p;
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
res = (res + query_seg(1, dfn[x], dfn[y])) % p;
return res % p;
}
- 因为一棵子树的 dfn 序是连续的,所以可以直接在线段树中修改:
void add_subtree(int x, int k)
{ k %= p; add_seg(1, dfn[x], dfn[x] + sze[x] - 1, k); }
- 求和同理,直接返回树上的区间和:
int query_subtree(int x)
{ return query_seg(1, dfn[x], dfn[x] + sze[x] - 1) % p; }
完整代码
点击查看代码
#include <bits/stdc++.h>
#define PII pair <int, int>
#define int long long
#define ls (x << 1)
#define rs ((x << 1) | 1)
#define mid (t[x].l + t[x].r >> 1)
#define fr(x, y, z) for(int x = y; x <= z; x ++ )
#define dfr(x, y, z) for(int x = y; x >= z; x -- )
using namespace std;
const int N = 1e6 + 10, M = N << 1;
int n, m, r, p, a[N], b[N];
int tot = 2, head[N], ver[M], nxt[M];
void add_edge(int x, int y)
{
ver[tot] = y;
nxt[tot] = head[x];
head[x] = tot ++ ;
}
int fa[N], dep[N], sze[N], w[N];
void dfs(int x, int f)
{
int mx = 0; sze[x] = 1;
fa[x] = f; w[x] = -1;
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to == f) continue;
dep[to] = dep[x] + 1;
dfs(to, x), sze[x] += sze[to];
if(mx < sze[to]) mx = sze[to], w[x] = to;
}
}
int dfn[N], cnt, top[N];
void dfs2(int x, int tp)
{
top[x] = tp;
dfn[x] = ++ cnt;
b[dfn[x]] = a[x];
if(w[x] == -1) return ;
dfs2(w[x], tp);
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to != fa[x] && to != w[x])
dfs2(to, to);
}
}
struct Node
{ int sum, ltg, l, r; } t[N << 2];
void add_point(int x, int k)
{
t[x].sum = (t[x].sum + k * (t[x].r - t[x].l + 1) % p) % p;
t[x].ltg = (t[x].ltg + k) % p;
}
void pushdown(int x)
{
int lt = t[x].ltg;
add_point(ls, lt), add_point(rs, lt);
t[x].ltg = 0;
}
void pushup(int x)
{ t[x].sum = (t[ls].sum + t[rs].sum) % p; }
void init(int x, int l, int r)
{
t[x] = {0, 0, l, r};
if(l == r) { t[x].sum = b[l] % p; return ; }
init(ls, l, mid), init(rs, mid + 1, r);
pushup(x);
}
void add_seg(int x, int l, int r, int k)
{
if(l <= t[x].l && t[x].r <= r)
{ add_point(x, k); return ; }
pushdown(x);
if(l <= mid) add_seg(ls, l, r, k);
if(mid < r) add_seg(rs, l, r, k);
pushup(x);
}
int query_seg(int x, int l, int r)
{
if(l <= t[x].l && t[x].r <= r)
return t[x].sum % p;
int res = 0;
pushdown(x);
if(l <= mid) res = (res + query_seg(ls, l, r)) % p;
if(mid < r) res = (res + query_seg(rs, l, r)) % p;
pushup(x);
return res % p;
}
int query_path(int x, int y)
{
int res = 0;
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]])
swap(x, y);
res = (res + query_seg(1, dfn[top[y]], dfn[y])) % p;
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
res = (res + query_seg(1, dfn[x], dfn[y])) % p;
return res % p;
}
void add_path(int x, int y, int k)
{
k %= p;
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]])
swap(x, y);
add_seg(1, dfn[top[y]], dfn[y], k);
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
add_seg(1, dfn[x], dfn[y], k);
}
int query_subtree(int x)
{ return query_seg(1, dfn[x], dfn[x] + sze[x] - 1) % p; }
void add_subtree(int x, int k)
{ k %= p; add_seg(1, dfn[x], dfn[x] + sze[x] - 1, k); }
signed main()
{
scanf("%lld%lld%lld%lld", &n, &m, &r, &p);
fr(i, 1, n) scanf("%lld", &a[i]);
int x, y;
fr(i, 1, n - 1)
{
scanf("%lld%lld", &x, &y);
add_edge(x, y), add_edge(y, x);
}
dep[r] = 1, dfs(r, 0);
dfs2(r, r);
init(1, 1, n);
fr(i, 1, m)
{
int opt, x, y, z;
scanf("%lld%lld", &opt, &x);
if(opt == 1) scanf("%lld%lld", &y, &z), add_path(x, y, z);
if(opt == 2) scanf("%lld", &y), printf("%lld\n", (query_path(x, y) % p + p) % p);
if(opt == 3) scanf("%lld", &z), add_subtree(x, z);
if(opt == 4) printf("%lld\n", query_subtree(x) % p);
}
return 0;
}
拓展
现在,已经了解用树剖 + 线段树维护区间点信息的方法,那如何对边权进行操作呢?
例题:P3038 [USACO11DEC] Grass Planting G
题目大意:给出一棵有 n 个节点的树,有 m 个如下所示的操作:
- 将两个节点之间的 路径上的边 的权值均加一。
- 查询两个节点之间的 那一条边 的权值,保证两个节点直接相连。
初始边权均为 0。
这道题的难点就是如何将边权转化为比较容易处理的点权,又因为树有特性:每一个非根节点都有且仅有一条通往父节点的边,所以可以将这条边的修改、查询下放至子节点。
那么修改或查询 \(u\) 到 \(v\) 的路径时,就需要去除 \(\operatorname{LCA}(u, v)\),带来的影响(因为 \(\operatorname{LCA}(u, v)\) 所代表的这条边并不在路径中)。
即将
add_seg(1, dfn[x], dfn[y], k);
query_seg(1, dfn[x], dfn[y]);
改为:
add_seg(1, dfn[x] + 1, dfn[y], k);
query_seg(1, dfn[x] + 1, dfn[y]);
但是这样又有可能会使线段树区间操作 \([l, r]\) 时 \(l > r\),所以需要在线段树的两个函数中特判,若 \(r > l\),则直接 return。
完整代码
点击查看代码
#include <bits/stdc++.h>
#define PII pair <int, int>
#define int long long
#define ST string
#define DB double
#define ls (x << 1)
#define rs ((x << 1) | 1)
#define mid ((t[x].l + t[x].r) >> 1)
#define fr(x, y, z) for(int x = y; x <= z; x ++ )
#define dfr(x, y, z) for(int x = y; x >= z; x -- )
using namespace std;
const int N = 1e6 + 10;
int n, m, q;
int tot = 2, head[N], ver[N << 1], nxt[N << 1];
void add(int x, int y)
{ ver[tot] = y; nxt[tot] = head[x]; head[x] = tot ++ ; }
int dep[N], w[N], fa[N], sze[N];
void dfs(int x, int f)
{
sze[x] = 1, w[x] = -1, fa[x] = f;
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to == f) continue;
dep[to] = dep[x] + 1;
dfs(to, x), sze[x] += sze[to];
if(w[x] == -1 || sze[to] > sze[w[x]]) w[x] = to;
}
}
int top[N], dfn[N], cnt;
void dfs2(int x, int tp)
{
top[x] = tp, dfn[x] = ++ cnt;
if(w[x] == -1) return ;
dfs2(w[x], tp);
for(int i = head[x]; i; i = nxt[i])
{
int to = ver[i];
if(to == fa[x] || to == w[x]) continue;
dfs2(to, to);
}
}
struct Node
{ int sum, tag, l, r; } t[N << 2];
void init(int x, int l, int r)
{
t[x] = {0, 0, l, r};
if(l == r) return ;
init(ls, l, mid);
init(rs, mid + 1, r);
}
void add_point(int x, int k)
{
t[x].sum += k * (t[x].r - t[x].l + 1);
t[x].tag += k;
}
void pushup(int x)
{ t[x].sum = t[ls].sum + t[rs].sum; }
void pushdown(int x)
{
if(!t[x].tag) return ;
add_point(ls, t[x].tag);
add_point(rs, t[x].tag);
t[x].tag = 0;
}
void add_seg(int x, int l, int r, int k)
{
if(r < l) return ;
if(l <= t[x].l && t[x].r <= r)
{ add_point(x, k); return ; }
pushdown(x);
if(l <= mid) add_seg(ls, l, r, k);
if(mid < r) add_seg(rs, l, r, k);
pushup(x);
}
int query_seg(int x, int l, int r)
{
if(r < l) return 0;
if(l <= t[x].l && t[x].r <= r)
return t[x].sum;
int res = 0;
pushdown(x);
if(l <= mid) res += query_seg(ls, l, r);
if(mid < r) res += query_seg(rs, l, r);
pushup(x);
return res;
}
void add_tr(int x, int y, int k)
{
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]]) swap(x, y);
add_seg(1, dfn[top[y]], dfn[y], k);
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
add_seg(1, dfn[x] + 1, dfn[y], k);
}
int query_tr(int x, int y)
{
int res = 0;
while(top[x] != top[y])
{
if(dep[top[x]] > dep[top[y]]) swap(x, y);
res += query_seg(1, dfn[top[y]], dfn[y]);
y = fa[top[y]];
}
if(dep[x] > dep[y]) swap(x, y);
res += query_seg(1, dfn[x] + 1, dfn[y]);
return res;
}
signed main()
{
scanf("%lld%lld", &n, &m);
int x, y;
fr(i, 2, n) scanf("%lld%lld", &x, &y), add(x, y), add(y, x);
dep[1] = 1, dfs(1, -1);
dfs2(1, 1);
init(1, 1, n);
ST op;
while(m -- )
{
cin >> op >> x >> y;
if(op[0] == 'P') add_tr(x, y, 1);
if(op[0] == 'Q') printf("%lld\n", query_tr(x, y));
}
return 0;
}
相关例题
详见该题单:树链剖分练习题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号