PID算法介绍和公式推导

PID算法概念

PID控制是一种常见的反馈控制算法，其名称来源于其使用的三个控制参数：比例（Proportional）、积分（Integral）和微分（Derivative）。

PID控制算法的目标是根据控制误差（即期望值与实际值之间的差异）来调整控制器输出，以使其尽可能接近期望值。

相关术语介绍

反馈：系统的输出成为输入的部分，反过来作用于系统本身，从而影响系统的输出，反馈分正反馈和负反馈。

开环：输入信号决定输出，输出不会影响系统输入。无反馈。

闭环：输出信号会被用来作为输入的一部分（反馈），输出影响系统的输入。

PID三个参数的作用

比例\(K_{p}\): P就是比例的意思。\(K_{p}\)越大，调节作用越激进，也就是说当前值和目标值相差较大时，可以将\(K_{p}\)调大，其实我们可以类比弹簧的运动。当物体距离平衡位置越远时，回复力越大，\(K_{p}\)起到的作用就相当于是回复力的作用。

微分\(K_{d}\): 可以设想一个弹簧：在平衡位置上，拉他一下，然后松手。这时候它会开始震荡，如果阻力很小，它会震荡很长时间才能重新停在平衡位置。
但如果我们给它一个阻尼作用，使得越接近目标时P的作用越柔和，也就是说K的作用就是刹住物理量的变化。

积分\(K_{i}\): 之前讨论的都是较为理想的情况，但现实生活中总会产生静态误差，比如给水加热时存在散热，汽车行驶时存在摩擦，因此如果只考虑P和D，最后达到的稳态很可能和预期的稳态存在一定偏差。这时候就需要引入

三者对应的时间关系： 专注现在（P）、总结过去（I）、预测未来（D）
比例环节：着眼于当下误差。
积分环节：累计过去所有误差，积分环节将过去的所有误差累加，最后乘以一个系数K_{i}。
微分环节:预测下一时刻误差。微分环节对当前时刻的误差求导,从而”预测”下一时刻的误差。在离散环境下，其数值等于此时的误差减去上一时刻的误差。

PID相关的数学公式和应用

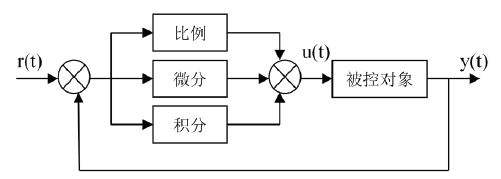
\(r(t)\)是要稳定的值。
\(y(t)\)是当前输出值。
\(e(t) = r(t) - y(t)\)
输入\(r(t)\)与输出\(y(t)\)进行比较，其差值\(e(t)\)经过PID控制器调整后输出电压控制信号\(u(t)\),\(u(t)\)经过被控对象后输出\(y(t)\)。

PID算法的标准式：

\[u(t) = K_{p}[e(t) + \frac{1}{T_{i}}\int_{0}^{t} e(t)dt + T_{D}\frac{de(t_)}{dt}] \]

t表示从开始调节到输出当前控制量所经过的时间间隔。

由于计算机只能处理数字信号，故将连续信号连续化，采样周期为T：

\[u(t) = K_{p}[e(k) + \frac{T}{T_{i}}\sum_{j=0} ^ {k}e_{j} + T_{D}\frac{e_{k}-e_{k-1}}{T}] \]

继续化简

\[\Rightarrow u(K) = K_{p} e(k) + K_{i}\sum_{j = 0}^{k}e_{j}+K_{D}[e(k)-e(k-1)] \]

\(\bullet\) 比例系数\(K_{P}\)

\(\bullet\) 积分系数\(K_{i}\)

\(\bullet\) 微分系数\(K_{D}\)

一种pid的简单实现代码如下

float location_pid_realize(_pid *pid, float actual_val) 
{
	//计算目标值与实际值的误差
    pid->err=pid->target_val-actual_val;  
    pid->integral += pid->err;    // 误差累积
	//PID算法实现
    pid->actual_val = pid->Kp*pid->err
		                  +pid->Ki*pid->integral
		                  +pid->Kd*(pid->err-pid->err_last);
  
	//误差传递
    pid->err_last=pid->err;
    //返回当前实际值
    return pid->actual_val;
}