[CF补题计划]Codeforces Round #813 (Div. 2) D

题意

给定长度为\(n\)的数组，可以进行\(k\)次操作，任意修改数组某个数字的值。用数组索引作为节点建图，对于两个数组索引\(i,j(i<j)\)，它们之间的无向边权值为 \(min(a[i],a[i+1],...a[j-1],a[j])\)，定义图的直径为\(max(d[i,j])\)，其中\(d[i,j]\)为\(i\)到\(j\)的最短路。求出在\(k\)次修改后的最大直径。

分析

一个性质 最短路的最大值一定在两个相邻位置取得。

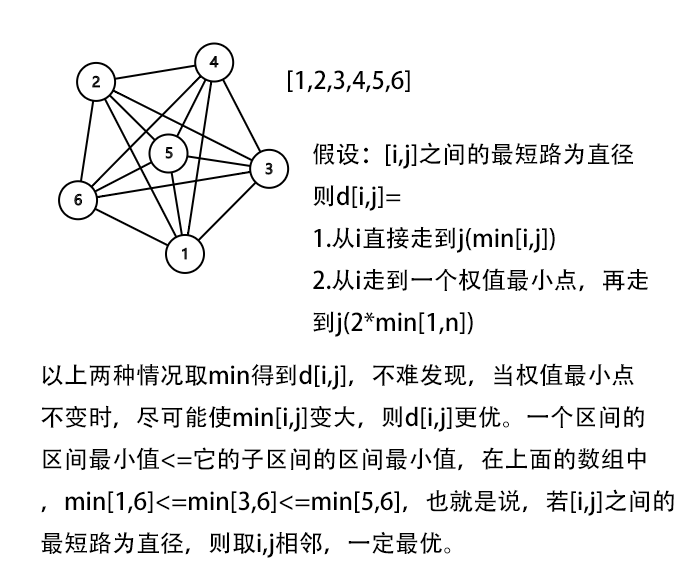
第一种做法（构造）

构造最长最短路

1. 期望最长最短路的取得方式为\(min(a[i],a[i-1])\)，使数组中最大值所在区间的较小值变为无穷大，取得原数组中最大权值的数字，剩下的\(k-1\)次修改直接将前\(k-1\)小的数字置为无穷大，计算此时的\(min（max(a[i]),min(a[i]*2))\)，记为\(ans1\)。

2. 期望最长最短路的取得方式\(min(a[i]*2)\)，直接将前\(k\)小的数字置为无穷大，计算此时的\(min(max(a[i]),min(a[i]*2))\)，记为ans2。

答案即为\(max(ans1,ans2)\)。

#include<bits/stdc++.h>
#define id first
#define v second
using namespace std;
const int N=2e5+100,inf=1e9;
int n,k,t;

bool cmp1(pair<int,int> a,pair<int,int> b)
{
	return a.id<b.id;
}

bool cmp2(pair<int,int> a,pair<int,int> b)
{
	return a.v<b.v;
}

main()
{
	cin>>t;
	while(t--)
	{
		vector<pair<int,int> > a;
		cin>>n>>k;
		int ans,ans1=inf,ans2=inf;
		for(int i=0;i<n;i++)
		{
			int x;cin>>x;
			a.push_back({i,x});
		}
		sort(a.begin(),a.end(),cmp2);
		
		for(int i=0;i<k-1;i++)
			a[i].v=inf;
		sort(a.begin(),a.end(),cmp2);
		ans1=min(ans1,a[0].v*2);
		ans1=min(ans1,a[n-1].v);
		
		a[0].v=inf;
		sort(a.begin(),a.end(),cmp2);
		ans2=min(ans2,a[0].v*2);
		sort(a.begin(),a.end(),cmp1);
		int p=-inf;
		for(int i=0;i<n-1;i++)
			p=max(p,min(a[i].v,a[i+1].v));
		ans2=min(ans2,p);
		
		ans=max(ans1,ans2);
		cout<<ans<<'\n';
	}
}

第二种做法（二分答案）

二分答案\(mid\)，表示\(k\)次修改后的直径。check函数判断是否存在一个点对，将直径修改为\(>=mid\)需要的最少次数\(<=k\)。
从\(i\)走到\(i+1\)有三种方法

1. 直接从\(i\)走到\(i+1\)，\(d[i,i+1]=min(a[i],a[i+1])\),所以\(i，i+1\)两个点的权值必须\(>=mid\)
2. 从\(i\)走到\(i\)前的某点，再走到\(i+1\)，\(d[i,i+1]=min(a[1,i-1]*2)\),所以\(i\)前的所有点的权值必须\(>=mid/2\)
3. 从\(i\)走到\(i+1\)后的某点，再走到\(i+1\)，\(d[i,i+1]=min(a[i+2,n]*2)\),所以\(i+1\)后的所有点的权值必须\(>=mid/2\)

check函数中预处理出前缀和后缀中点权\(*2<=mid\)的个数，再枚举一遍所有相邻点对的最小修改次数，判断是否\(<=k\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100,inf=1e9;
int a[N],n,k,t;
int cnt1[N],cnt2[N];
bool check(int mid)
{
	for(int i=0;i<=n+1;i++) cnt1[i]=0,cnt2[i]=0;
	int ans=1e9;
	for(int i=1;i<=n;i++)
	{
		cnt1[i]=cnt1[i-1];
		if(a[i]*2<mid) cnt1[i]++;
	}
	for(int i=n;i;i--)
	{
		cnt2[i]=cnt2[i+1];
		if(a[i]*2<mid) cnt2[i]++;
	}
	for(int i=1;i<=n-1;i++)
	{
		int x=0;
		if(a[i]<mid) x++;
		if(a[i+1]<mid) x++;
		x+=cnt1[i-1]+cnt2[i+2];
		ans=min(ans,x);
	}
	return ans<=k;
}
main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>t;
	while(t--)
	{
		cin>>n>>k;
		for(int i=1;i<=n;i++) cin>>a[i];
		int l=1,r=1e9;
		while(l<r)
		{
			int mid=l+r+1>>1;
			if(check(mid)) l=mid;
			else r=mid-1;
		}
		cout<<l<<'\n';
	}
}