[区间dp] P1622 释放囚犯

题意

一条线段上有\(P\)个点，要求你添加\(Q\)个断点，第\(i\)个断点为\(a[i]\)。每次切割断点的代价为这个断点所在的线段的点个数-1，问切割所有断点所需的最小代价。

数据范围

\(1≤P≤10^{3},\ 1≤Q≤100,\ Q≤P\)

分析

想了半天感觉肿么线性dp都没法转移状态，看题解懵逼哎呀肿么就区间dp了捏，然后看到大佬题解恍然大悟，呜呜菜菜

我们将问题转化，先将所有断点切割，此时线段状态↓

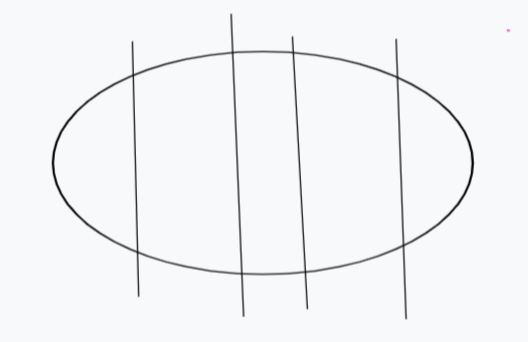
随后我们再将断点添加回来，耗费的代价即是断点左右两部分的点数个数。

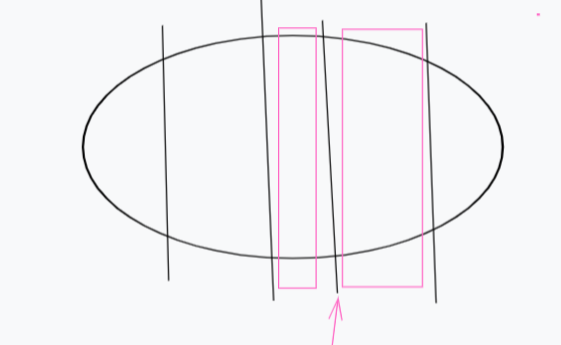
添加回来后，线段就变成了↓

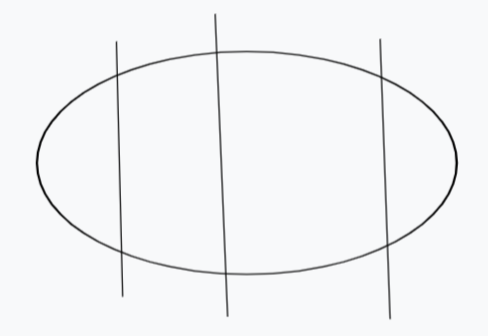
以此类推继续添加断点，直到线段恢复初始状态。

namo，我们就把这个问题转化成了类似石子合并的区间dp问题，接下来只要注意细节的处理就ok了。

状态表示

\(f[l][r]\)表示从第\(l\)个断点一直添加到第\(r\)个断点所需耗费的最小代价，可得状态转移式

\(f[l][r]=min(f[l][r],f[l][k-1]+f[k+1][r]+a[r+1]-a[l-1]-1-1)\)

细节问题

处理前先将\(a\)数组排序，断点符合有序性才能保证转移方程正确

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int f[N][N],a[N];
int n,m;
main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>a[i];
	sort(a+1,a+1+m);
	a[m+1]=n+1;
	for(int len=1;len<=m;len++)
	{
		for(int l=1;l<=n-len+1;l++)
		{
			int r=l+len-1;
			f[l][r]=1e8;
			for(int k=l;k<=r;k++)
				f[l][r]=min(f[l][r],f[l][k-1]+f[k+1][r]+a[r+1]-a[l-1]-2);
		}
	}
	cout<<f[1][m];
}

呜呜呜晚上就热身赛了我这种蒟蒻还只能写绿题……