灰度插值算法

灰度插值算法

---

1. 简介

灰度值插值是图像变换中必不可少的方法，因为图像并非连续函数，而是经过数字化的 —— 即由与（离散）灰度值相关联的像素组成。例如，当对图像进行旋转和下采样时（如图 1.1 所示），输出图像的某个像素将不再精确对应输入图像中的单个像素，而是可能包含原始图像中多个像素的部分信息。因此，需要一种方法来计算输出像素的灰度值。一种可能的方法是仅使用原始图像中单个像素的灰度值（例如，中心最接近输出像素中心的那个像素），但这意味着原始图像中的信息可能会在变换过程中丢失，进而导致图像质量下降。另一种选择是在原始图像的多个像素灰度值之间进行插值。

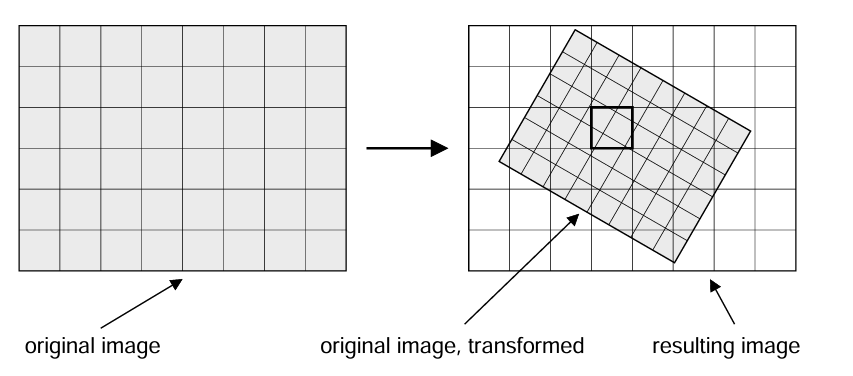
图 1.1：由旋转和下采样组成的图像变换

---

2. 插值方法

2.1 概述

• 'nearest_neighbor'（最近邻)：速度快但质量低，仅用于实时性要求高的场景。

• 'bilinear'（双线性）：考虑4邻域像素，适合无缩放的旋转/放大。

• 'constant'（常数）/'weighted'（加权）：集成平滑的多步插值，适合任意缩放场景。

• 'bicubic'（双三次）：基于16邻域的高质量插值，适合高精度放大。

2.1.1 图像变换插方法对比

方法	质量	运行时间（相对）	推荐用途
nearest_neighbor	低	1x	实时应用
bilinear	高（放大）	3x	无需缩放的旋转/放大
constant	中（缩放均衡）	3x（放大）10x（缩小）	需平衡缩放质量的场景
weighted	高（缩小）	3x（放大）20x（缩小）	高质量缩小需求
bicubic	极高（放大）	6x	高精度放大需求

2.2 最近邻插值

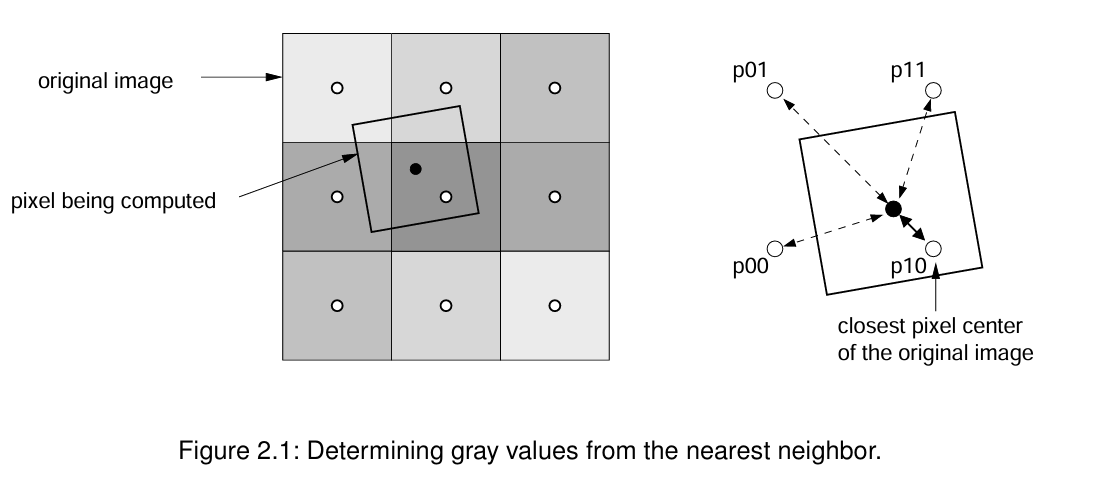
如果选择 “最近邻”（nearest_neighbor）插值方法，则不会对多个像素进行插值。相反，输出像素会被赋予原始图像中中心位置最接近输出像素中心的像素的灰度值。此过程如图 2.1 所示：

在此示例中，输出像素获取像素 p10 的灰度值。最近邻插值是确定输出像素灰度值的最简单、最快的方法。但通常情况下，若对图像进行旋转或缩放，该方法会导致 混叠（aliasing）和锯齿边缘（jagged edges） 等不良效果。

2.3 双线性插值

如果选择“双线性”（bilinear）插值方法，则使用双线性插值确定灰度值。与最近邻插值不同，双线性插值的灰度值由四个相邻像素决定，如图2.2所示。

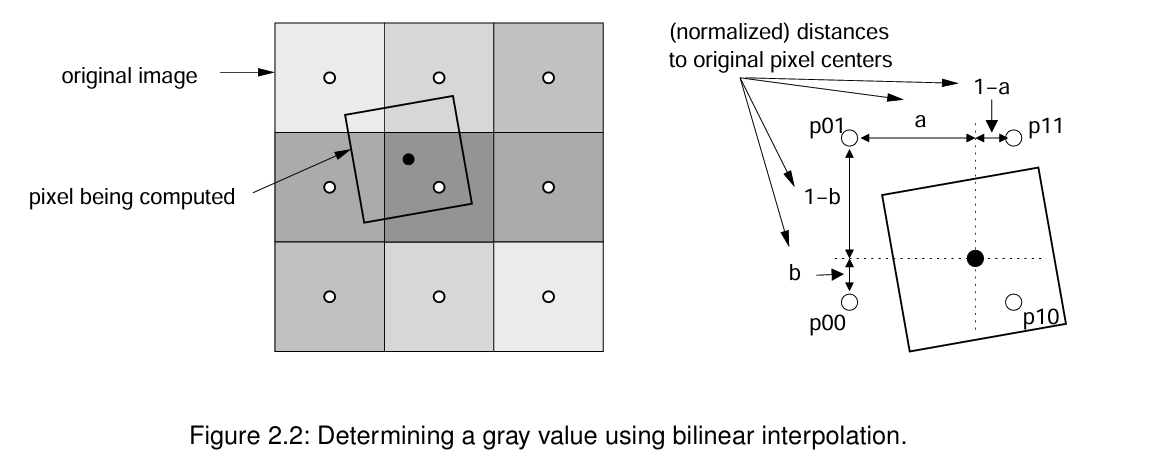
相邻像素的影响取决于其中心与输出像素中心的距离。因此，首先需要计算变换后坐标与相邻像素中心的水平和垂直距离。然后，按以下公式计算输出灰度值：

$$
\text{hres} = b \cdot (a \cdot h_{11} + (1-a) \cdot h_{01}) + (1-b) \cdot (a \cdot h_{10} + (1-a) \cdot h_{00})
$$

 

其中，(\text{hres}) 表示输出像素的灰度值，(h_{ij}) 表示相邻像素的灰度值。

由于输出灰度值受四个相邻像素的共同影响，双线性插值比最近邻插值产生的图像更平滑，但计算时间也更长。

注意：如果对图像进行下采样，双线性插值可能因混叠效应导致意外结果。若需要高质量的下采样图像，应使用带集成平滑的插值方法（见2.4节）。

2.4 集成平滑的双线性插值

若图像变换包含下采样（缩小）操作，可能出现所谓的混叠效应（aliasing effects）。这种效应由信息丢失导致，会在下采样图像中产生不期望的伪影。

为减少混叠影响，需在缩小图像前进行平滑处理，例如使用均值滤波或高斯滤波。另一种方式是将平滑处理集成到灰度值插值过程中，选择插值方法'constant'或'weighted'时会自动完成这一操作。以下章节将详细介绍带集成平滑的插值方法。

2.4.1 等权重双线性插值（'constant'）

选择'constant'时，使用等权重双线性插值确定灰度值。为减少下采样图像的混叠效应，平滑处理通过以下步骤集成到插值中：

1. 子采样（Subsampling）： 首先对输出像素进行子采样，即将其划分为多个部分。如图2.3所示，相对于输入图像的像素，反向变换后的输出像素大小为[1.5,1.5]，在每个方向上采样两次。

2. 样本点灰度计算： 在输入图像中通过双线性插值确定每个样本点的灰度值。

3. 均值计算： 最终输出像素的灰度值为所有样本点灰度值的平均值。

    

2.4.2 高斯加权双线性插值（'weighted'）

如果选择 'weighted'，则使用高斯加权双线性插值来确定灰度值。与等权重插值类似，灰度值插值分三步执行：二次采样、确定采样点的灰度值，以及根据所有采样点的灰度值计算最终的灰度值。

然而，对于 'weighted' 插值，采用了不同的采样和加权方法。主要区别在于，现在将比像素更大的区域划分为更多的子像素（见图 2.4）。每个采样点的灰度值确定方式与 'constant' 方法相同，即通过双线性插值。不过，与 'constant' 方法使用等权重不同，这里应用了高斯平滑。图 2.4 展示了生成像素在 3×3 位置采样时的加权情况。

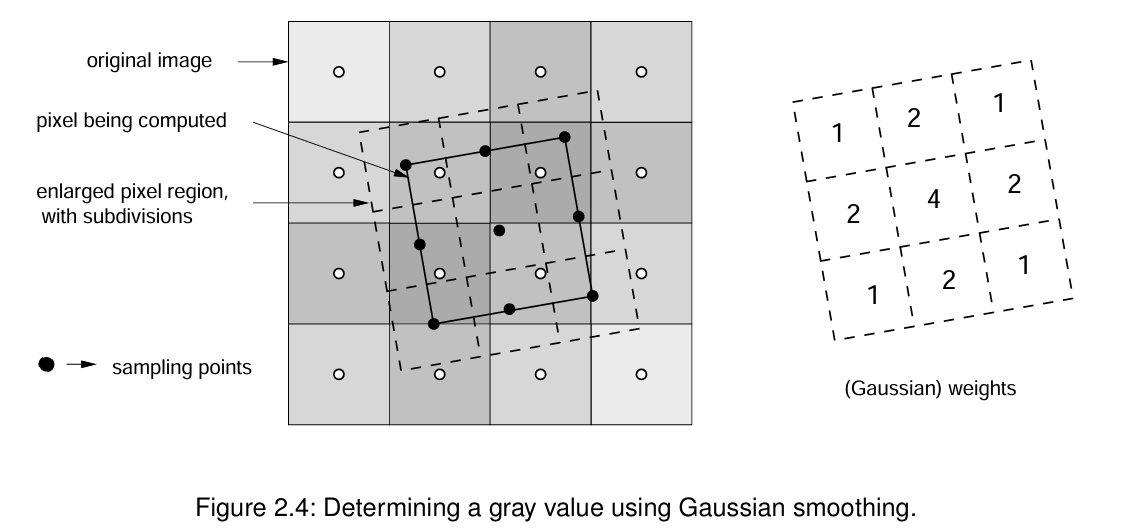
'weighted' 插值方法大致相当于在二次采样前用高斯滤波器对图像进行平滑处理。与等权重双线性插值相比，这种插值方法生成的输出图像外观更平滑。不过，对于降采样图像，其运行时间会显著增加。

关键对比

方法	平滑方式	样本点权重	计算成本	输出平滑度
'constant'	等权重均值	均匀权重	中	中等
'weighted'	高斯核加权	中心像素权重更高	高	更高

总结：带集成平滑的插值方法通过子采样和权重分配减少混叠，适用于需要高质量下采样的场景，其中'weighted'以更高计算成本换取更优平滑效果。

• 'constant'：等权子采样平均，减少缩小时的混叠。

• 'weighted'：高斯加权子采样，平滑效果更优但耗时更长。

2.5 双三次插值

双三次插值会考虑图像中最近对应像素周围的16 个像素的加权平均值，基于这 16 个像素的灰度值构建一个双三次多项式曲面，再通过该曲面确定目标（亚）像素位置的灰度值。与双线性插值或最近邻插值相比，此方法能产生更平滑的插值结果，且插值伪影更少。

需要注意的是，得到的灰度值可能超出给定图像的灰度值范围。如果选择插值方法 'bicubic_clipped'，这些灰度值将被裁剪到输入图像的灰度值范围内。然而，这种方法仅适用于确定特定位置的灰度值。

请注意，如果图像进行降采样，由于混叠效应，双三次插值可能会导致意外结果。为减少这些不良影响，如果需要高质量的降采样图像，应使用结合平滑处理的插值方法（见第 10 页的 2.4 节）。

2.6 系统参数int_zooming

影响灰度值插值质量和速度的另一种方式由系统参数'int_zooming'决定。该参数决定图像变换是使用整数运算还是浮点运算。当'int_zooming'设置为'true'时，内部使用定点运算来执行变换。这会使执行时间大幅缩短。然而，它会略微降低变换后灰度值的准确性。此外，对于某些算子，可能会出现灰度值未定义的像素。在某些情况下，定义域区域也可能会因'int_zooming'的值而略有不同。如果'int_zooming'设置为'false'，则使用浮点运算来执行变换。这会带来更精确的计算。对于字节图像，两种计算方式的差异通常小于两个灰度级。相应地，对于int2和uint2图像，如果使用16位的整个动态范围，灰度值差异可能高达512个灰度级。

• 'true'：使用整数运算加速，精度略有损失。

• 'false'：浮点运算确保精度，适用于16位图像。

'int_zooming'的值默认设置为'true'。要更改此值，可以使用算子set_system 。

系统参数'int_zooming'会影响以下算子：图像的几何变换（projective_trans_image、projective_trans_image_size、affine_trans_image、affine_trans_image_size、polar_trans_image_ext、polar_trans_image_inv和rotate_image）、灰度值缩放scale_image 以及图像的放大或缩小zoom_image_factor和zoom_image_size。

---

3. 示例

3.1 旋转

在图3.1展示的第一个示例中，对图像进行无缩放的纯旋转时，比较了最近邻插值、双线性插值和双三次插值的结果。

图3.1a)展示了包含钞票序列号的原始图像，其中字符不是水平的。使用“最近邻”, “双线性”和“双三次”插值方法对图像进行旋转，使序列号变为水平。

图3.1b)展示了使用最近邻插值进行旋转的结果。在细节视图中，可以清楚地看到字符边缘典型的、不期望的锯齿状外观。

图3.1c)展示了使用双线性插值进行旋转的结果。现在字符的边缘看起来非常平滑。这是因为双线性插值在确定最终灰度值时考虑了四个相邻像素，而不是仅一个像素。请注意，对于纯图像旋转，“双线性”“constant”和“weighted”插值方法的结果是相同的。

图3.1d)展示了使用双三次插值进行旋转的结果。对于无放大的纯旋转，其结果与双线性插值的结果非常相似。

• 最近邻：字符边缘锯齿明显。

• 双线性：边缘平滑，质量显著提升。

• 双三次：与双线性结果相近，但放大时更优。

3.2 放大

图 3.2 展示的示例说明了一个图像变换的效果，该变换包含放大 10 倍的操作。这里比较了 “最近邻”, “双线性” 和 “双三次” 插值方法的结果。图 3.2a) 展示了要变换的图像，它显示了一个保持架的一部分。为了更好地展示结果，仅显示图 3.2a) 中标记细节的放大视图。

图 3.2b) 展示了使用最近邻插值的结果。原始图像的像素结构清晰可见。

图 3.2c) 展示了使用双线性插值的结果。虽然边缘看起来平滑得多，但仍能察觉到原始图像的像素结构。请注意，对于放大操作，“双线性插值”， “constant” 和 “weighted” 插值方法的结果是相同的。

图 3.2d) 展示了使用双三次插值的结果。边缘看起来几乎完全平滑，原始图像的像素结构不再可见。

• 最近邻：像素块明显。

• 双线性：边缘仍有锯齿。

• 双三次：边缘近乎完美平滑。

图 3.2：使用不同插值方法进行图像放大的结果对比（b）最近邻插值（'nearest_neighbor'）（c）双线性插值（'bilinear'）（d）双三次插值（'bicubic'）

3.3 缩小

图 3.3 展示的示例说明了一个图像变换的效果，该变换包含以 0.1 的缩放因子进行缩小操作。这里比较了 “最近邻”“双线性”“constant”“weighted” 和 “双三次” 插值方法的结果。图 3.3a 展示了要变换的图像，它显示了两个物体，左边是一个安全环，右边是一个齿轮。为了更好地展示结果，针对每种插值方法都给出了每个物体的细节视图。

图 3.3b 展示了使用最近邻插值进行图像缩小的结果。这种过采样缩小的结果质量较差。特别是在细节视图中，可以看出形状往往几乎是直的，而原始图像中相同部分的形状则完全不同且带有圆角。

图 3.3c 展示了使用双线性插值进行图像缩小的结果。与最近邻插值相比，质量略有提高，但形状上仍存在严重的失真。

图 3.3d 展示了使用 constant 插值进行图像缩小的结果。缩小后的图像比双线性插值的结果更接近原始图像。与双线性插值相比，缩小后图像的质量显著提高。

图 3.3e 展示了使用带有集成高斯滤波器的 weighted 插值进行图像缩小的结果。与 constant 插值相比，图像更平滑，形状几乎与原始形状一致。在细节视图中可以看到，边缘的渐变也更精细。因此，weighted 插值的结果与双三次插值的结果非常相似。

图 3.3f 展示了使用双三次插值进行图像缩小的结果。对于缩小操作，双三次插值为包含缩小的图像变换提供了最佳质量。

• 最近邻/双线性：形状失真严重。

• constant/weighted：保留形状且平滑，后者更优。

• 双三次：缩小效果类似双线性，不推荐。

图 3.3：使用 “最近邻”、“双线性”、“常数”、“加权” 和 “双三次” 插值进行图像下采样的结果对比

该图展示了不同插值方法在图像下采样（缩小）时的效果差异，重点体现混叠效应和细节保留能力：

• 最近邻插值（nearest_neighbor）： 下采样后边缘锯齿严重，细节丢失明显，混叠效应显著（如棋盘格伪影）。

• 双线性插值（bilinear）： 边缘平滑度优于最近邻，但仍存在轻微混叠，细节模糊（如纹理过渡不自然）。

• 常数插值（constant）： 通过等权重均值平滑减少混叠，边缘更柔和，细节损失较少，优于双线性插值。

• 加权插值（weighted）： 采用高斯加权平滑，混叠效应进一步降低，图像整体更平滑，细节保留较好（如边缘过渡自然）。

• 双三次插值（bicubic）： 下采样质量较高，细节较清晰，但仍可能因缺乏显式平滑导致轻微混叠（需结合2.4节方法进一步优化）。

关键结论：

• 下采样时，带集成平滑的插值方法（constant/weighted） 显著优于无平滑方法（最近邻/双线性/双三次），能有效抑制混叠。

• 加权插值（weighted） 在平滑与细节平衡上表现最佳，适合高质量下采样需求（如医学影像、遥感图像处理）。

---

通过实际示例可见，不同插值方法在速度与质量间存在权衡，需根据具体应用场景选择。