模式识别笔记1-贝叶斯决策论

1. Bayes Rule

贝叶斯公式：

\[p(\omega|x)=\frac{p(x|\omega)p(\omega)}{p(x)} \]

2. Bayes Error Rate

对于贝叶斯分类器：

• if \(p(\omega_1|x)>p(\omega_2|x), \textrm{ decide } \omega_1\)
• Otherwise, decide \(\omega_2\)

所以2分类分类器误差为：

\[p(error|x)=min[p(\omega_1|x),p(\omega_2|x)] \]

所以n分类为：

\[p(error|x)=1-max[p(\omega_1|x),p(\omega_2|x,...,p(\omega_n|x))] \]

直观展示：

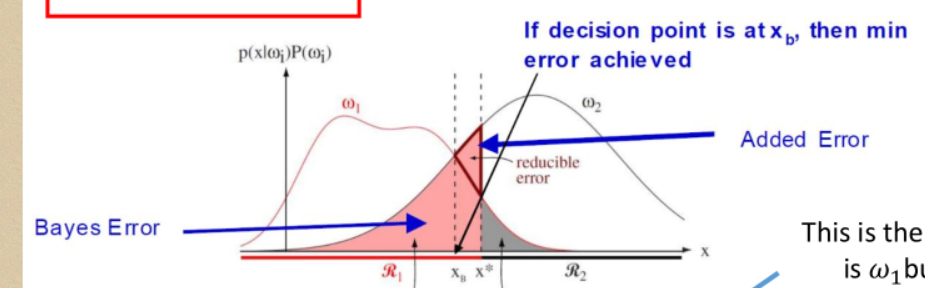
用积分的思想：

\[\begin{align} \notag p(error) & =p(x\in R_2, \omega_1)+ p(x\in R_1, \omega_2)\\ &=p(x\in R_2|\omega_1)p(\omega_1)+p(x\in R_1|\omega_2)p(\omega_22)\\ \notag &=\int_{R_2}p(x|\omega_1)p(\omega_1)dx+\int_{R_1}p(x|\omega_2)p(\omega_2)dx \end{align} \]

决策边界不在鞍点，则会产生reducible error(可还原误差)

3. 损失函数

假定：

• \(c\)个分类{\(\omega_1\),\(\omega_2\),...,\(\omega_c\)}
• \(a\)个可能的操作\(\{\alpha_1,\alpha_2,...,\alpha_a\}\),比如选择去看病or不去(课程中的例子)
• \(\lambda_{ij}=\lambda(\alpha_i|\omega_i)\)表示分类是\(\omega_j\)的时候采取操作\(\alpha_i\)带来的损失

对于给定的观察状态\(x\)，若它的真实分类为\(w_j\)，而我们选择了操作\(\alpha_i\)，其损失则是\(\lambda_{ij}\)

进一步的，对于所有的可能的状态，对于选择了操作\(\alpha_i\)其损失(Conditional risk)为：

\[R(\alpha_i|x)=\sum_j^c{\lambda_{ij}p(\omega_j|x)} \]

自然的，对于所有可能的观察，总体误差(overall risk)为：

\[err = \int{R(\alpha(m)|x)p(x)dx} \textrm{ for }m\in [1,a] \]

显然只要\(R(\alpha_i|x)\)d达到最小，则总体误差最小。

举个例子，对于一个二分类问题：

\[\notag \begin{align} R(\alpha_1|x) &=\lambda_{11}p(\omega_1|x)+\lambda_{12}p(\omega_2|x)\\ \notag R(\alpha_2|x)&=\lambda_{21}p(\omega_1|x)+\lambda_{22}p(\omega_2|x) \end{align} \]

4. 判别式函数Discriminant Function

对于贝叶斯分类器，可以把它视作是一组判别式函数的集合（共\(c\)个判别器，代表一个类一个）：

\[\notag g_i(x), i=1,...,c \]

如果 $ g_i(x)>g_j(x) \textrm{ for all }j\neq i$ ,状态\(x\)会被归为类别 \(\omega_i\)。

当然判定函数的选择不唯一：对于上述的集合，可以定义一个单调递增函数 \(G:\)

\[G(g_i(x)) > G(g_j(x)) \textrm{ if }g_i(x)>g_j(x) \textrm{ for all } j\neq i\notag \]

例如，可以是log函数:

\[\begin{array} \notag G(g_i(x))&=\ln(g_i(x))\\ &=\ln(p(\omega_i|x))\\ &=\ln(\frac{p(x|\omega_i)p(\omega_i)}{p(x)})\\ &=\ln(p(x|\omega_i))+\ln(p(\omega_i))-\ln(p(x)) \end{array} \]

其中\(p(x|\omega_i)\)的\(p\)可以是高斯分布(即正态分布)

5 正态分布 Normal Distribution

先上正态分布公式:

\[p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp[-\frac{1}{2}(\frac{x-\mu}{\sigma})^2] \]

其中\(\sigma​\)是标准差，\(\mu​\)是期望。

推广到多维度，对于维度\(d\):

\[\begin{array}{} p(x)=\frac{1}{(2\pi)^{\frac{d}{2}}|\sum|^\frac{1}{2}}\exp[-\frac{1}{2}(x-\mu)^T{\Sigma}^{-1}(x-\mu)]\\ \textrm{Where }\\ x=(x_1,x_2,...,x_d)^T\\ \mu=(\mu_1,\mu_2,...,\mu_d)^T\\ \Sigma = \int (x-\mu)(x-\mu)^Tp(x)dx \end{array} \]

5.1 多元正态密度函数下的判别函数

回顾一下我们的判别函数(公式(7))：

\[\notag g_i(x)=\ln(p(x|\omega_i))+\ln(p(\omega)) \textrm{ with } p(\omega_i) \textrm{ is ignored} \]

则基于多元正态密度函数下的判别函数为:

\[g_i(x)=-\frac{1}{2}(x-\mu_i)^T{\Sigma}^{-1}(x-\mu_i)-\frac{d}{2}\ln(2\pi)-\frac{1}{2}\ln|\Sigma_i|+\ln(p(\omega_i))\\ \textrm{if } p(x|\omega_i)\sim N(\mu_i,\Sigma_i) \]

• 假设对于所有类别的数据，协方差相同，即\(\Sigma_i = \Sigma\)

  则判别函数(10)可以简化为：

  \[g_i(x)=-\frac{1}{2}(x-\mu_i)^T{\Sigma_i}^{-1}(x-\mu_i)+\ln{p(\omega_i)} \]

  进一步的，对于公式(11)，前半项拆分：

  \[\notag -\frac{1}{2}(x-\mu_i)^T{\Sigma_i}^{-1}(x-\mu_i)= -\frac{1}{2}{\Sigma_i}^{-1}(x^Tx-2\mu_ix+\mu_i^T\mu_i)\\ \]

  注意到 \(x^T{\Sigma_i}^{-1}x\) 独立于 \(i\) ，可以忽略，因此公式(11)可以进一步化简:

  \[\begin{array}{} g_i(x)&={\Sigma_i}^{-1}\mu_ix--\frac{1}{2}{\Sigma_i}^{-1}\mu_i^T\mu_i+\ln(\omega_i)\\ &=w_i^Tx+w_{i0} \end{array} \]

  可以看到这其实是一个线性判别函数，在样本空间里直观地感受下：
  

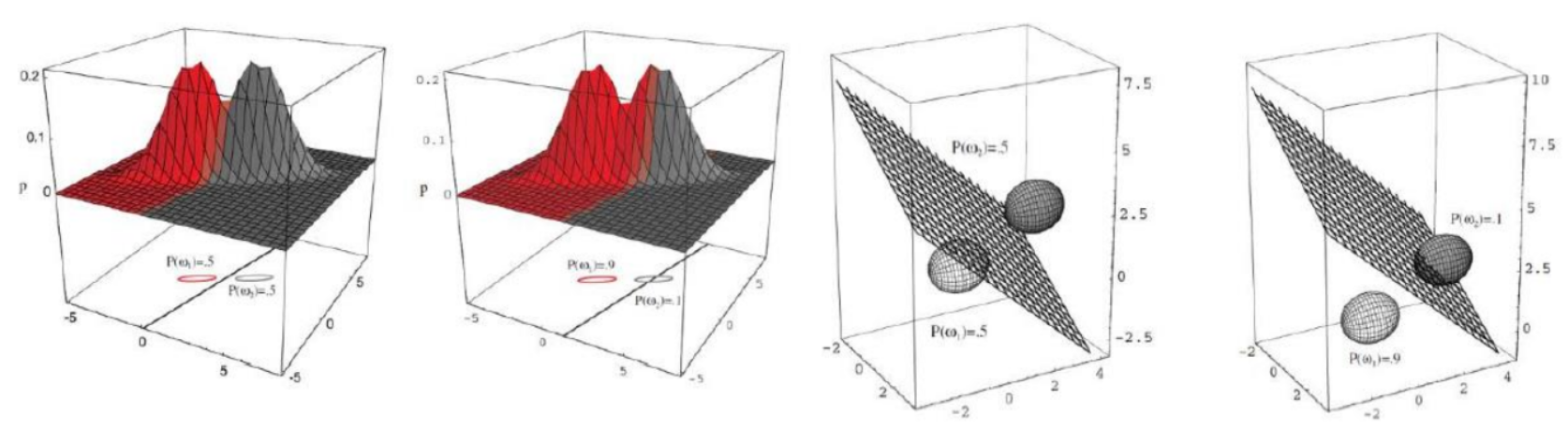
• 假设协方差不同

  则：

  \[\begin{array}{rl} g_i(x)&=x^TW_ix+w_ix+w_{i0}\\ \textrm{where }& \\ W_i &= -\frac{1}{2}\Sigma_i^{-1},\\ w_i& = \Sigma_i^{-1}\mu_i,\\ w_{i0}&=-\frac{1}{2}\mu^T\Sigma^{-1}_i\mu-\frac{1}{2}\ln|\Sigma_i|+\ln p(\omega_i) \end{array} \]

  ​

6 极大似然估计 Maximum Likelihood

上一小节假定样本对于每种类概率分布遵循高斯分布，则公式(12)的有两个参数需要估计，分别是\(\sum_i\)和\(\mu_i\)。即我们需要估计\(p(x|\omega_i)\)这一高斯分布(即正态分布)的参数，从而根据一个观察值 \(x\)，我们能迅速知道其最可能所属类别。

假定某种分布的优势在于：把问题从估计某种未知的后验函数简化为估计已知分布函数的参数

极大似然估计的优势：

• 简单
• 在样本量增加时能够收敛

我们假定:

• 样本集合 ${x_j}= D $ 中的每个样本独立同分布，基于概率函数 \(p(x|\omega_j)\)
• \(p(x|\omega_j)\sim N(\mu_j,\Sigma_j)\) ，即服从正态分布

则\(p(x|\omega_j)=p(x|\omega_j,\theta_j) \textrm{ where }\theta_j=(\mu_j, \Sigma_j)\)其中\(\theta_j\)维度与总类别个数有关，即\((j=1,2,...,c)\)

我们的目标：使用 \(n\) 个样本来估计参数 \(\theta_j\)

基于上面的假设，由于 \(D\) 由 \(n\) 个独立的样本组成，则有：

\[p(D|\theta)=\prod_{k=1}^np(x_k|\theta) \]

其中：

• \(p(D|\theta)\) 称作 \(\theta\) 关于样本的可能性。
• 极大似然估计对于 \(\theta\) 的估计即是最大化 \(p(D|\theta)\)
• 根据贝叶斯决策理论，最大化后验概率 \(p(x_k|\theta)\) 将产生最小的误差

公式(13)的连乘难以处理，并且有可能浮点溢出，可以做一个对数处理：

\[\begin{array}{rl} l(\theta)&=\ln(p(D|\theta))\\ &=\sum_{k=1}^n\ln(p(x_k|\theta)) \end{array} \]

则极大化似然的 \(\theta\) 即：

\[\widehat{\theta}=arg\max_{\theta}l(\theta) \]

最优化的一个必要条件：

\[\begin{array}{} \nabla_\theta l = \sum_{k=1}^n\nabla_\theta\ln(p(x_k|\theta))=0\\ \textrm{where }\nabla_\theta=\left [\frac{\partial}{\partial\theta_1},...,\frac{\partial}{\partial\theta_p}\right]^T \end{array} \]

6.1 Case: 未知 \(\mu\)，\(\Sigma​\) 已知

即已知 \(p(x_i|\mu)\sim N(\mu, \Sigma)\)

回顾2.5节我们的正态分布概率密度函数:

\[\notag p(x)=\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}}\exp\left [ -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right] \]

则它的似然函数Log-likelihood：

\[\notag \sum_{k=1}^n\ln(p(x_k|\mu))=\sum_{k=1}^n\left (-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)-\frac{d}{2}\ln(2\pi)-\frac{1}{2}\ln(|\Sigma|)\right) \]

根据极大化似然估计，最优的 \(\hat{\mu}\) 满足:

\[\notag \nabla_\mu\sum_{k=1}^np(x_k|\mu)=\sum_{k=1}^n\Sigma^{-1}(x_k-\hat{\mu})=0 \]

于是:

\[\notag \sum_{k=1}^n(x_k-\hat{\mu})=0\Rightarrow \hat{\mu}=\frac{1}{n}\sum_{k=1}^nx_k \]

6.2 Case: \(\mu\) 和 \(\sigma\) 均未知

即 \(p(x_i|\mu,\sigma^2)\sim N(\mu,\Sigma)\)

类似的：

\[\notag \begin{array}{} \nabla_\mu\sum_{k=1}^np(x_k|\mu,\sigma)&=\sum_{k=1}^n\Sigma^{-1}(x_k-\hat{\mu})\\ \nabla_\sigma\sum_{k=1}^np(x_k|\mu,\sigma)&=\sum_{k=1}^n\left (-\frac{1}{\hat{\sigma}}+\frac{(x_k-\hat{\mu})^2}{{\hat{\sigma}^2}} \right) \end{array} \]

则最优的 \(\hat{\mu}\) 和 \(\hat{\sigma}\) 为：

\[\begin{array}{} \hat{\mu}&=\frac{1}{n}\sum_{k=1}^nx_k\\ \hat{\sigma}^2&=\frac{1}{n}\sum_{k=1}^n(x_k-\hat{\mu})^2 \end{array} \]

6.3 如何使用ML训练分类器

假定:

• 给定训练集 \(D\)
• \(D = (x_k, y_k)\)，其中 \(k=1,2,\cdots, n\)表示数据维度为 \(n\)；\(y_k={\omega_1,\omega_2,\cdots,\omega_c}\)表示共 \(c\) 个类

方法:

• 将训练集 \(D\) 划分为 \(D_i\) , 其中 \(i=1,\cdots,c\) ，样本集 \(D_i\) 属于类别 \(\omega_i\)
• 使用每个 \(D_i\) 对每个类别分别估计参数 \(\mu_i\) 和 \(\Sigma_i\)
• \(g_i(x)\) 取决于参数 \(\mu_i\) 和 \(\Sigma_i\)

6.4 一个例子

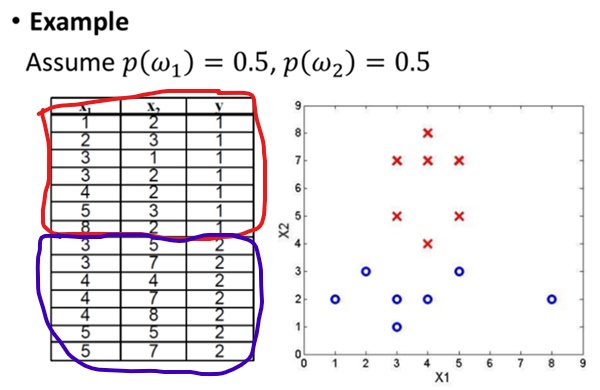
由公式(17): \(\hat{\mu}=\frac{1}{n}\sum_{k=1}^nx_k, \hat{\sigma}^2=\frac{1}{n}\sum_{k=1}^n(x_k-\hat{\mu})^2\)可知：

\[\notag \begin{align} \hat{\mu_1} &= (3.71,2.14)^T, & \hat{\mu_2} &= (4.00,6.14)^T \\ \notag \hat{\sigma}^2_1 &= (4.49,0.41)^T, & \hat{\sigma}^2_2 &= (0.57,1.84)^T \\ \notag \widehat{\Sigma}_1&= \begin{pmatrix} 4.49& 0\\ 0& 0.41 \end{pmatrix}, & \widehat{\Sigma}_2&= \begin{pmatrix} 0.57& 0\\ 0& 1.84 \end{pmatrix} \\ \notag \widehat{\Sigma}^{-1}_1&= \begin{pmatrix} 0.22& 0\\ 0& 2.44 \end{pmatrix},& \widehat{\Sigma}^{-1}_2&= \begin{pmatrix} 1.75& 0\\ 0& 0.54 \end{pmatrix} \end{align} \]

回顾我们的判别式函数(公式13):

\[\notag \begin{array}{rl} g_i(x)&=x^TW_ix+w_ix+w_{i0}\\ \textrm{where }& \\ W_i &= -\frac{1}{2}\Sigma_i^{-1},\\ w_i& = \Sigma_i^{-1}\mu_i,\\ w_{i0}&=-\frac{1}{2}\mu^T\Sigma^{-1}_i\mu-\frac{1}{2}\ln|\Sigma_i|+\ln p(\omega_i) \end{array} \]

得出

\[\notag \begin{array} {} g_1(x) &=-0.11x_1^2-1.22x_2^2+0.82x_1+5.22x_2-8.1 \\ g_2(x) &= -0.87x_1^2-0.27x_2^2+7.02x_1+3.34x_2-24.9 \end{array} \\ \Downarrow \\ \text{Decision boundary:}\\G(x)=g_1(x)-g_2(x)=0.76x_1^2-0.95x_2^2-6.20x_1+1.88x_2+16.8 \]

即